Кинетический момент тела, вращающегося относительно неподвижной точки.

Скорость точек тела, вращающегося относительно неподвижной точки, определяется формулой 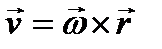или в проекциях на оси декартовой системы координат

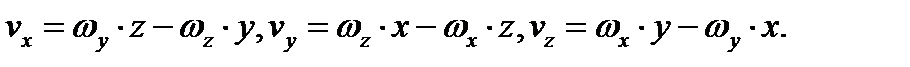
Подставляя полученные формулы в выражение (3.16), получаем

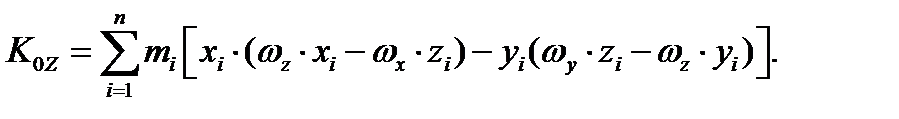(3.23)

Раскрывая полученные произведения и приводя подобные члены при проекциях угловых скоростей, заметим, что мы получаем одинаковые сомножители типа

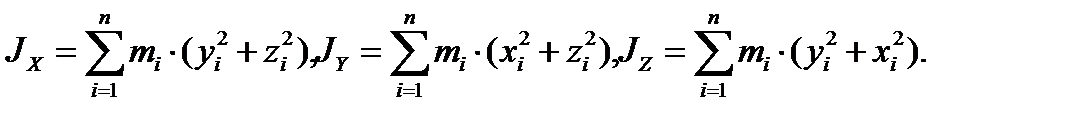(3.24)

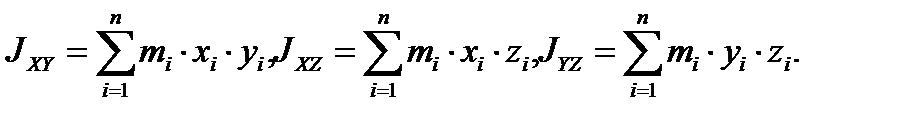(3.25)

Выражения, задаваемые формулами (3.24) носят названия осевых моментов инерции. Моментом инерции системы материальных точек относи­тельно оси называется сумма произведений масс этих точек на квадраты их расстояний до оси,а (3.25) – центробежных моментов инерции. Формулы (3.24) и (3.25) для сплошного твёрдого тела можно записать в интегральной форме

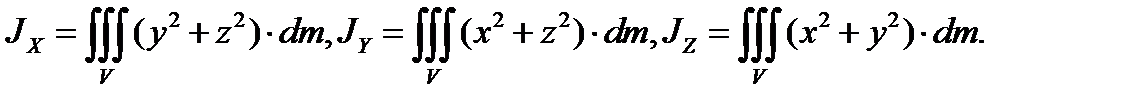(3.26)

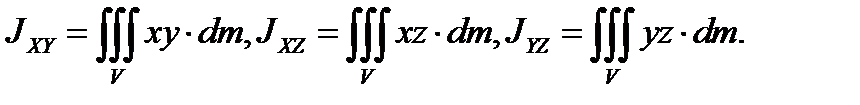(3.27)

Тройной интеграл берётся по объёму всего тела. Подставим полученные моменты инерции в (3.23)

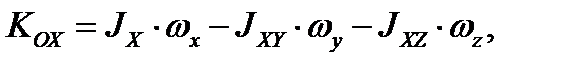
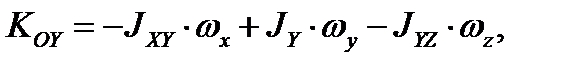(3.27)

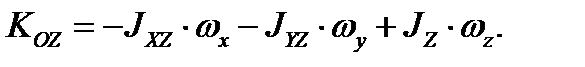
Выражение (3.27) можно представить в матричной форме

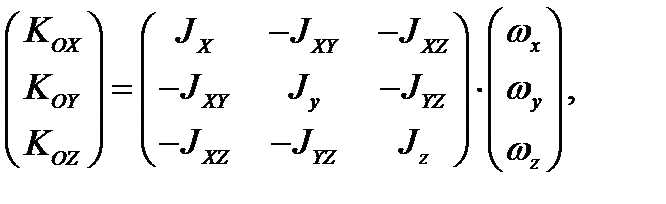
здесь 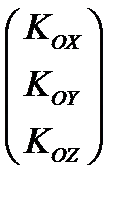- вектор столбец кинетического момента, 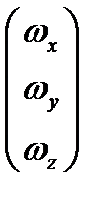- вектор столбец угловой скорости, а 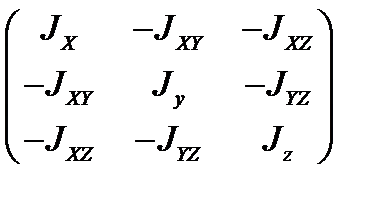- матрица моментов инерции тела.