Динамики относительного движения точки.

Предположим, что система координат Oxyz может быть при­нята за абсолютную (неподвижную или галилееву) систему и что в этой системе координат движение точки определяется дифферен­циальным уравнением

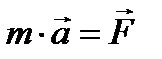
где 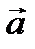обозначает абсолютное ускорение точки. Чтобы составить уравнение движения по отношению к другой системе координат 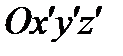, движущейся заданным образом по отношению к абсолютной системе, вспомним кинематическую зависимость между абсолютным ускорением 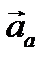и относительным ускорением :

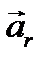(3.11)

где 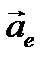— переносное ускорение, т. е. ускорение того пункта си­стемы 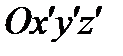, через который проходит в данный момент рассматри­ваемая движущая точка, 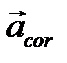- кориолисово ускорение точки, обу­словленное вращательным движением относительной системы 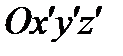по отношению к абсолютной системе Oxyz (гл 8,§3).

,

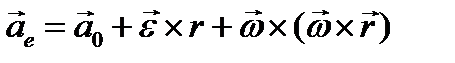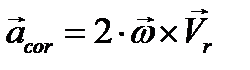
Подставляя значение ускорения 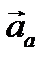из (3.11) в основное уравнение, получим:

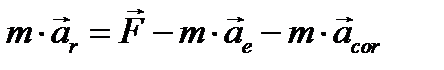
Введем обозначения: 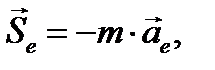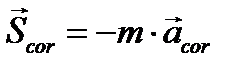, и условимся в дальнейшем опускать индекс « 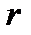» у элементов относи­тельного движения; тогда последнее равенство примет вид

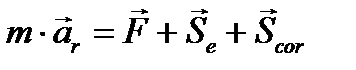(3.12)

Вектор 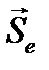называется пере­носной силой инерции, а 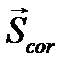- поворотной или кориолисовой силой инерции. Анализ формулы (3.12) приводит к следующему выводу: дифференциальные урав­нения динамики относительного движения составляются так же, как и в абсолютной системе, только к непосредственно прило­женным силам присоединяются еще силы инерции — переносная и кориолисова.

Если относительная система 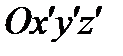движется по отношению к абсолютной системе Oxyz поступательно, прямолинейно и равно­мерно, то она представляет галилееву систему, т. е. уравнение движения в ней не должно ничем отличаться от уравнения движения в абсолютной системе; действительно, в этом случае 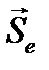= =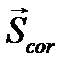0, так что уравнение (3.12) совпадает с основным уравнением. В случае плоского движения относительной системы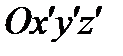

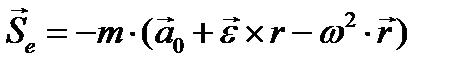
при равномерном вращении (ε = 0) относительной системы вокруг неподвижной или равномерно и поступательно движущейся по от­ношению к абсолютной системе оси ( 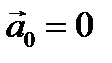) получим: 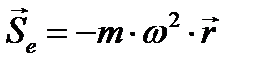, ( это центробежная сила). Кориолисова сила не будет входить в формулы относительного движения, если относительная система движется поступательно ( = 0) или если в силу характера связей точка вынуждена дви­гаться параллельно оси вращения ( 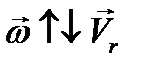). Из уравнения относительного движения легко получить уравне­ния относительного равновесия. Для этого достаточно в формуле (3.12) положить 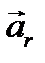= = 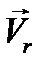0; тогда уравнение относитель­ного равновесия будет: 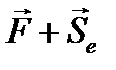=0.

Все, что сейчас говорилось по отношению к точке, может быть перенесено на случай любой системы точек. Прикладывая силы инерции, мы можем рассмотрение движения в относительной си­стеме координат свести к тем же уравнениям, что и в абсолютной.

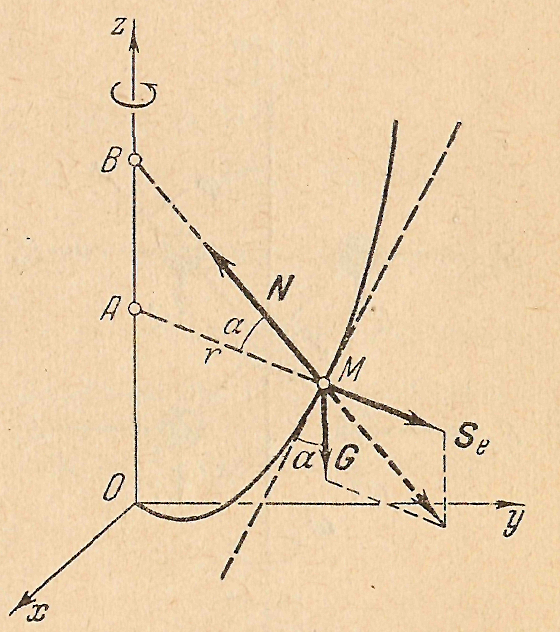
Пример 1. Найти условие относи­тельного равновесия тяжелой точки на глад­кой кривой данной формы, вращающейся равномерно вокруг вертикальной оси с угловой скоростью ω. Каков должен быть Рис 51

вид кривой для того, чтобы в любом положении на кривой точка была в относительном равновесии (рис. 51) Решение задачи сводится к примене­нию метода кинетостатики. Точка М нахо­дится в относи тельном равновесии под влиянием сил: веса G, центробежной силы , где 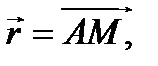и реакции кривой 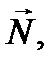которая направлена по нормали 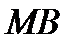к кривой. Написав условие равновесия в проекции на касательную, получим:

G cos а — Se sin a = 0,

или после подстановки значения Se:

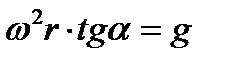
Отрезок rtg а = АВ представляет поднормаль кривой r = f(z), на которой находится точка М, и условие равновесия дается равенством 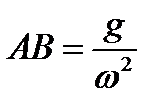. Заменяя 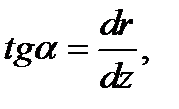перепишем условие относительного равновесия в виде

. (3.13)

Подставив 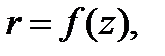получим значение ординаты 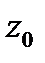, в которой при данном 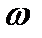будет иметь место равновесие.

Для решения второго вопроса проинтегрируем уравнение (3.13). Найдем уравнение параболы: 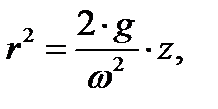при вращении этой параболы с угловой ско­ростью 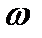тяжелый шарик будет в любой ее точке находиться в состоянии безразличного отно­сительного равновесия. Как известно, свободная поверхность жидкости в сосуде, приведённом во вращение, принимает форму параболоида.

Пример 2. Относительное равновесие тяжелой точки вблизи поверхности Земли. Найдем условия относительного равновесия груза на нити (отвеса), принимая во внимание вращение Земли. Притяжение F (рис.51а) груза Землей искажается действием центробежной силы Se, так что вес тела, равный натяжению нити N, не будет равен F; кроме того, направление отвеса DM не совпадает с направлением радиуса МО Земли в данном пункте. Обозначим геоцентрическую широту, т. е. угол радиуса Земли с плоскостью земного экватора через λ, а гео­графическую широту, т. е. угол отвесной линии с той же плоскостью, через φ. Уравнение относительного равновесия записываются в виде

,

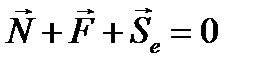проектируя силы на кажущуюся горизонталь НН, получим:

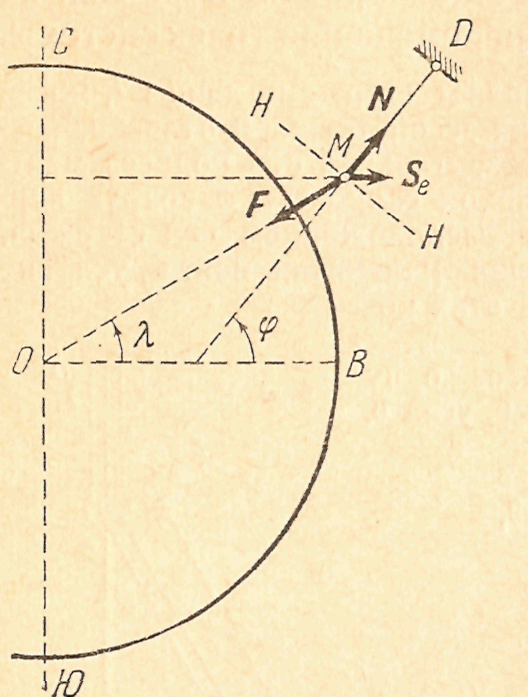Заменим здесь Se и F по формулам 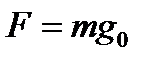, где m — масса груза, R — средний радиус Земли, 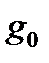- ускорение, вызываемое притяжением Земли; это ускорение не следует смешивать с кажущимся ускорением g, т. е. ускорением 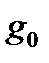, искаженным центробежной силой. После замены получим:

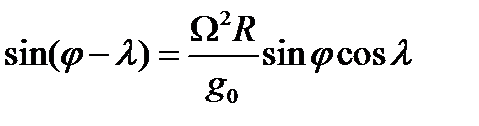
Замечая, что угловая скорость Земли 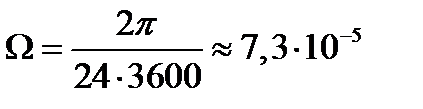1/сек, радиус Земли R=6350000м и ускорение 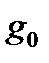=9,81 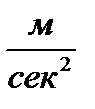, получим:

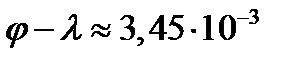
так что разность 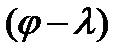очень мала и предыдущее уравнение можно записать в виде

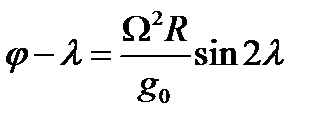Рис 51а

максимальное значение этой разности при φ= 45° будет:

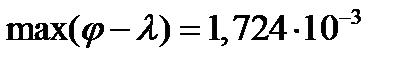
что соответствует приблизительно 6'.

Проектируя силы на направление отвеса DM, найдем:

N= mg = F cos (φ -λ) — Se cosφ

или, вследствие малости угла (φ -λ), 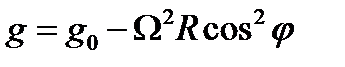. Отсюда легко найти относительную разность между 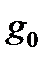и g: Максимальное значение это отношение имеет на экваторе (φ = 0):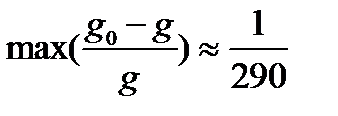

Если бы Земля вращалась примерно в 17 раз быстрее, то тела на экваторе не имели бы веса.

Переносной силой инерции, вызванной вращением Земли, объясняется также и сжатие Земли. Земля имеет форму геоида, т.е. тела, нормаль к поверхности которого совпадает в каждой точке с линией отвеса. Поверхность геоида можно заменить эллипсоидом вращения, сжатие которого по данным измерений равно .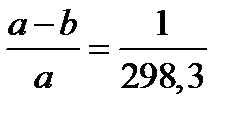

Вопросы для самопроверки.

1. Напишите векторную формулу динамики относительного движения точки, что такое силы инерции.

2. Напишите векторную формулу силы сопротивления среды, прокомментируйте введенные обозначения.

3. Напишите в самом общем виде дифференциальные уравнения движения точки (в декартовой системе координат).

4. Напишите дифференциальные уравнения движения точки в осях натурального триэдра.

α

h

L

5. Сколько (и какие) необходимо задать начальных условий для определения движения точки (в декартовой системе координат)?

6. С какой абсолютной скоростью сойдет колечко со стержня, если его длина равна L , начальное положение 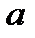, угловая скорость вращения стержня ω. Стержень перпендикулярен оси вращения.

7. В чем разница между прямой и обратной (основной) задачами динамики?

8. Напишите уравнение относительного равновесия точки..

9. Составьте дифференциальное уравнения относительного движения колечка по стержню, вращающемуся с постоянной угловой скоростью ω, трение не учитывать.

10. Чему равно время движения точки на участке горизонтального

прямолинейного движения, если начальная скорость 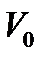, а конечная 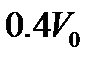? Сила сопротивления среды равна .

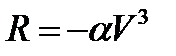11. Чему равен путь, пройденный точкой, на участке горизонтального прямолинейного движения, если начальная скорость 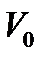, а конечная 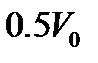? Сила сопротивления среды равна .

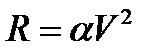Глава 10.