Представление графов в памяти компьютера

Представление графов в памяти компьютера существенно зависит от типов структур данных, допускаемых используемым алгоритмическим языком и типом компьютера. Представление с помощью матрицы смежности ‑ одно из самых распространенных. Для графов с большим числом дуг это достаточно компактное представление, особенно если есть возможность работать с двоичными битами в машинном слове. К недостаткам следует отнести большой расход памяти при работе с графами, имеющими небольшое число дуг (матрица смежности при этом получается весьма разреженной), а также невозможность уменьшения трудоемкости алгоритмов в том случае, когда она пропорциональна числу дуг, а не числу вершин.

Матрица смежности неориентированного графа симметрична относительно главной диагонали, поэтому достаточно хранить в памяти только половину ее.

Задание графа с помощью матрицы смежности удобно и тогда, когда граф взвешенный и элементами матрицы являются не нули и единицы, а веса дуг. Пример задания ориентированного и неориентированного графов матрицами смежности приведен на рис. 4.2.

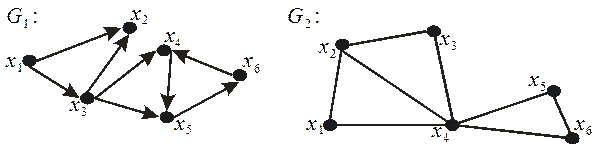
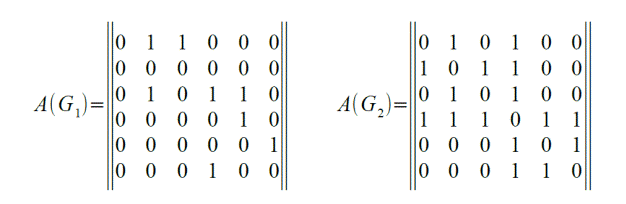
Рис. 4.2. Задание ориентированного и неориентированного графов матрицами смежности.

Представление с помощью матрицы инциденций определяет граф однозначно (с точностью до изоморфизма), но применяется крайне редко в силу большой разреженности матрицы и практического отсутствия алгоритмов, работающих на такой структуре данных.

Представление с помощью списков смежности является основной альтернативой представлению с помощью матрицы смежности. Список смежности для вершины v ‑ это список концов дуг, исходящих из вершины 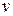в случае орграфа, или список смежных с 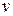вершин в случае графа. Граф представляется с помощью 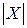списков смежности, по одному для каждой вершины. Если число дуг в орграфе существенно мало по сравнению с полным графом, то этот сподоб представления весьма эффективен. Списки смежности занимают объем памяти 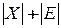и легко реализуются с помощью списочных структур. Менее удобен этот способ представления для задания взвешенных графов, так как тогда возникает необходимость хранения весов дуг и установления соответствующих связей между дугами и их весами.

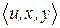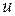Пример задания графов, показанных на рис. 4.2, с помощью списков смежности приведен на рис. 4.3. Представление с помощью списка дуг применяется в тех случаях, когда необходимо иметь отдельную, независимую нумерацию дуг. При этом способе каждой дуге сопоставляется тройка , где ‑ дуга, 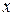‑ ее начало, 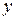‑ ее конец. Этот способ представления легко обобщается на случай взвешенных графов. Более того, он наиболее приспособлен для хранения различной информации о дугах.

Пусть 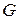‑ неориентированный граф, 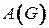‑ его матрица смежности. Так как 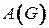симметрична относительно главной диагонали, будем рассматривать только ее верхнюю треугольную часть 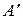. Запишем строки 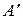последовательно одну за другой и найдем двоичное число, соответствующее полученной последовательности из нулей и единиц. Меняя нумерацию вершин, будем для одного и того же графа получать разные числа. Наибольшее из них носит название кода Xapapи.

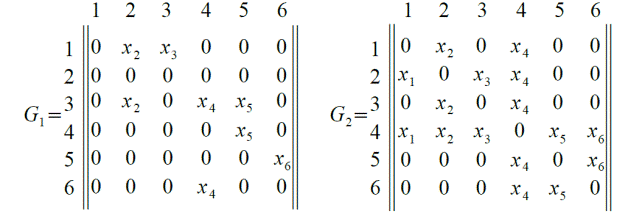
Рис. 4.3. Списки смежности графов на рис. 4.2.

Код Харари определяет граф однозначно, поэтому, например, задачу определения изоморфизма двух графов можно свести к сравнению соответствующих кодов Харари[3].

Нумерация вершин (и матрица смежности), соответствующая коду Харари, носит название канонической и используется при перечислении (генерировании) графов с заданными свойствами.

Наиболее распространенным методом сбора информации о строении графа является специальным образом организованный обход вершин и дуг (ребер) графа [5]. Информация, получаемая таким способом, оформляется в виде подходящей нумерации вершин.