Поиск в глубину в графе
Идея метода поиска в глубину[5]состоит в следующем. Поиск в обыкновенном графе 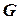 начинается с некоторой начальной вершины
начинается с некоторой начальной вершины 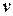 (с этого момента
(с этого момента 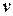 считается просмотренной). Пусть
считается просмотренной). Пусть 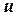 ‑ последняя просмотренная вершина (этой вершиной может быть и
‑ последняя просмотренная вершина (этой вершиной может быть и 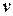 ). Тогда возможны два случая.
). Тогда возможны два случая.
1) Среди вершин, смежных с 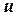 , существует еще непросмотренная вершина
, существует еще непросмотренная вершина 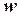 . Тогда
. Тогда 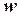 объявляется просмотренной, и поиск продолжается из вершины
объявляется просмотренной, и поиск продолжается из вершины 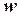 . Будем говорить, что вершина
. Будем говорить, что вершина 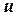 является отцом вершины
является отцом вершины 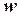 (
( 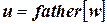 ). Ребро
). Ребро 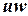 в этом случае будет называться древесным.
в этом случае будет называться древесным.
2) Все вершины, смежные с 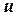 , просмотрены. Тогда и объявляется использованной вершиной. Обозначим через
, просмотрены. Тогда и объявляется использованной вершиной. Обозначим через 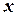 ту вершину, из которой мы попали в
ту вершину, из которой мы попали в 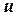 , т. е.
, т. е. 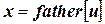 ; ноиск в глубину продолжается из вершины
; ноиск в глубину продолжается из вершины 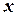 .
.
Если в графе 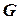 не осталось непросмотренных вершин, то поиск заканчивается. Если же осталась непросмотренная вершина
не осталось непросмотренных вершин, то поиск заканчивается. Если же осталась непросмотренная вершина 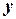 , то поиск продолжается из этой вершины.
, то поиск продолжается из этой вершины.
Поиск в глубину просматривает вершины графа 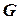 в определенном порядке. Для того чтобы зафиксировать этот порядок, будет использоваться массив
в определенном порядке. Для того чтобы зафиксировать этот порядок, будет использоваться массив 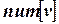 . При этом естественно считать, что
. При этом естественно считать, что 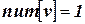 , если
, если 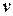 начальная вершина, и
начальная вершина, и  , если
, если 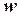 просматривается сразу после того, как просмотрена вершина
просматривается сразу после того, как просмотрена вершина 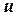 .
.
Пусть в обыкновенном графе 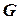 проведен поиск в глубину. Обозначим через
проведен поиск в глубину. Обозначим через 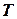 множество всех древесных ребер. Все остальные ребра графа будем называть обратными ребрами. Множество всех обратных ребер обозначим через
множество всех древесных ребер. Все остальные ребра графа будем называть обратными ребрами. Множество всех обратных ребер обозначим через 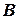 .
.
Результат применения поиска в глубину к связному графу 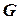 (рис.4.4 а) показан на рис. 4.4 b. Здесь сплошные линии изображают древесные ребра, а пунктирные линии ‑ обратные ребра.
(рис.4.4 а) показан на рис. 4.4 b. Здесь сплошные линии изображают древесные ребра, а пунктирные линии ‑ обратные ребра.
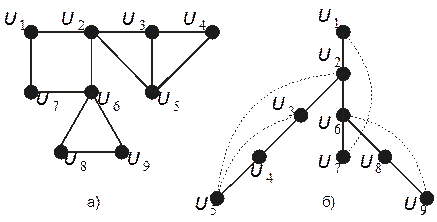
Рис. 4.4. a) Связный граф; b) Результат применения поиска в глубину к связному графу.
Нумерация вершин соответствует порядку, в которым они просматриваются поиском в глубину. Можно заметить, что множество всех древесных ребер с выделенной начальной вершиной 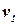 образует корневое дерево с корнем
образует корневое дерево с корнем 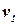 , которое дерево часто называют глубинным деревом или
, которое дерево часто называют глубинным деревом или 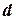 -деревом графа
-деревом графа 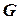 [5]. Отметим, что каждое обратное ребро соединяет в
[5]. Отметим, что каждое обратное ребро соединяет в 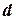 -дереве предка и потомка.
-дереве предка и потомка.
Отметим несколько свойств поиска в глубину, введя предварительно два определения. Будем называть дуги, пройденные при поиске в глубину дважды (в прямом и обратном направлениях), отмеченными, а путь 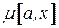 из начала обхода
из начала обхода 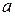 в текущую вершину
в текущую вершину 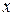 , не содержащий отмеченных дуг,— текущим путем.
, не содержащий отмеченных дуг,— текущим путем.
Свойство 1. После завершения обхода орграфа при поиске в глубину частичный граф, образованный отмеченными дугами, есть корневое ордерево с корнем в начале обхода.
Свойство 2. Для того, чтобы после завершения обхода орграфа при поиске в глубину все вершины оказались пройденными, необходимо и достаточно, чтобы обход начинался во входе и этот вход был единственным. При этом корневое ордерево, образованное отмеченными дугами, имеет множество вершин, совпадающее со всем множеством вершин графа, и тем самым является каркасом графа, называемым деревом поиска в глубину.
Свойство 3. Текущий путь есть простой путь в орграфе. Его можно продолжить либо до тупикового, т. е. заканчивающегося висячей вершиной, либо до циклического, т, е. до встречи с уже пройденной вершиной.
Пусть 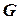 ‑ несвязный граф,
‑ несвязный граф, 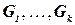 ‑ множество всех его компонент связности. Обозначим через
‑ множество всех его компонент связности. Обозначим через  множество древесных ребер, выделенных поиском в глубину в компоненте
множество древесных ребер, выделенных поиском в глубину в компоненте 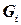 , а через
, а через 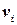 ‑ корневую вершину из
‑ корневую вершину из 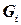 , т.е. первую просмотренную вершину подграфа
, т.е. первую просмотренную вершину подграфа 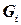 . Таким образом, множество всех древесных ребер несвязного графа образует остовный лес. Фиксируя в каждом поддереве этого леса корневую вершину, мы получим глубинный лес или
. Таким образом, множество всех древесных ребер несвязного графа образует остовный лес. Фиксируя в каждом поддереве этого леса корневую вершину, мы получим глубинный лес или 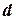 -лес графа
-лес графа 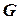 .
.
Представим теперь формальное описание указанного алгоритма. В алгоритме используются описанные ранее массивы 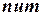 и
и 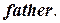 В процессе работы алгоритма массив
В процессе работы алгоритма массив 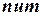 используется для распознавания непросмотренных вершин, а именно, равенство
используется для распознавания непросмотренных вершин, а именно, равенство 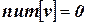 означает, что вершина
означает, что вершина 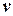 еще не просмотрена.
еще не просмотрена.
Изложим версию алгоритма поиска в глубину, основанную на рекурсивной процедуре 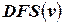 [6], осуществляющей поиск в глубину из вершины
[6], осуществляющей поиск в глубину из вершины 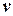 .
.
Алгоритм поиска в глубину.
1. procedure DFS(v);
2. begin
3. num[v] := i; i := i + 1;
4. for 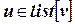 do
do
5. if 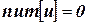 then
then
6. begin
7. 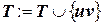 ; father[u] := v; DFS(u)
; father[u] := v; DFS(u)
8. end
9. else if num[u] < num[v] and 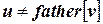 then
then
10. 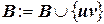
11. end;
12. begin
13. i := 1; 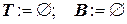 ;
;
14. for 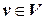 do
do 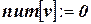 ;
;
15. for 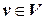 do
do
16. if 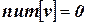 then
then
17. begin
18. 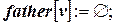 DFS(v)
DFS(v)
19. end
20. end.
4.1.3. Задачи о покрытиях графов.
Задача о реберном покрытии.
Определение 4.23. Множество ребер 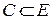 образует реберное покрытие графа
образует реберное покрытие графа 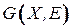 , если каждая вершина
, если каждая вершина 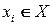 инцидентна хотя бы одному из ребер множества
инцидентна хотя бы одному из ребер множества 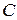 .
.
Покрытие с минимальным числом ребер называется минимальным (оптимальным).
Рассмотрим простой пример графа, изображенного на рис. 4.5.
В этом примере  ,
, 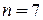 , номера ребер указаны на рисунке в кружочках. Множество ребер
, номера ребер указаны на рисунке в кружочках. Множество ребер 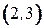 не образует реберное покрытие, так как вершины 2 и 5 не инцидентны ни одному из ребер этого одному из ребер этого множества. Множество ребер (1, 4, 6) образует реберное покрытие.
не образует реберное покрытие, так как вершины 2 и 5 не инцидентны ни одному из ребер этого одному из ребер этого множества. Множество ребер (1, 4, 6) образует реберное покрытие.
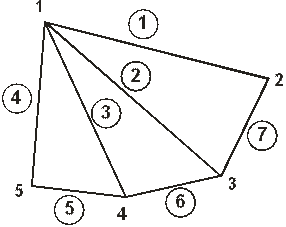
Рис. 4.5. Пример графа.
Матрица инциденций графа имеет вид
Сформулируем модель целочисленного программирования для поиска минимального покрытия графа. Введем 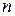 бинарных переменных:
бинарных переменных:

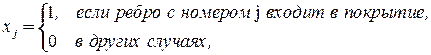
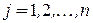 .
.
Тогда целевая функция имеет вид
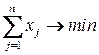 ,
,
условия инцидентности для всех вершин запишутся в виде
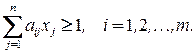
В задаче о взвешенном реберном покрытии каждое ребро 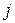 характеризуется весом
характеризуется весом 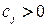 . В этой задаче целевая функция имеет вид
. В этой задаче целевая функция имеет вид
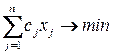 (4.1)
(4.1)
Задача о паросочетаниях. Пусть число вершин 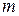 графа четно. Под паросочетанием (совершенным) понимается такое множество попарно несмежных ребер, что каждая вершина графа инцидентна одному ребру из этого множества.
графа четно. Под паросочетанием (совершенным) понимается такое множество попарно несмежных ребер, что каждая вершина графа инцидентна одному ребру из этого множества.
Если паросочетание существует, то число ребер в нем равно 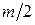 . Оптимальным называется паросочетание с минимальной суммой весов входящих в него ребер. Целевая функция в задаче о паросочетаниях имеет вид (4.1), а ограничения имеют вид:
. Оптимальным называется паросочетание с минимальной суммой весов входящих в него ребер. Целевая функция в задаче о паросочетаниях имеет вид (4.1), а ограничения имеют вид:
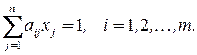
Здесь
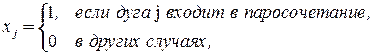
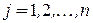 .
.
Задача об оптимальном реберном покрытии разрешима для любого связного симметричного графа. В то же время задача о паросочетаниях разрешима не всегда. В частности, она может оказаться неразрешимой, если степени всех вершин нечетны. Но если задача о паросочетаниях разрешима, то ее оптимальное решение есть допустимое решение задачи о реберном покрытии. Поэтому значение целевой функции для оптимального решения задачи о паросочетаниях является верхней оценкой для оптимального решения задачи о реберном покрытии.
Дата добавления: 2016-06-05; просмотров: 3504;











