Амплитудно-импульсный элемент и его эквивалентное представление.

Простейшую импульснуюсистему можно представить в виде соединения импульсного элемента и непрерывной части. Рассмот­рим амплитудно-импульсный элемент (АИЭ). Импульсный элемент представляет собой устройство, на выходе которого в момент времени t=0,T, … nT, … наблюдается последовательность импульсов произвольной формы с амплитудами, пропорциональными дискретам входного сигнала x[nT]. Обозначение АИЭ в схемах и соответствующие при этом друг другу входной и выходной сигналы пока­заны на рис.5.

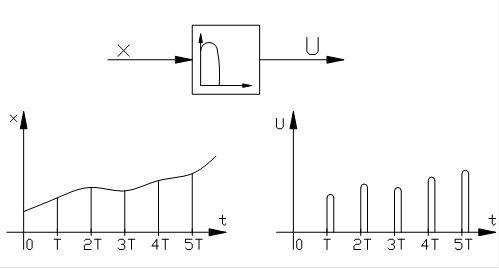Рис. 5

При математическом описании ИЭ оказывается удобным поня­тие идеального импульсного элемента (ИИЭ). Под идеальным им­пульсным элементом будем понимать звено, выходная величина x*(t) которого представляет собой последовательность 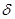-функций с площадями, равными дискретам входной величины х[nT] . Пусть функция s(t) задает форму импульса на выходе ИЭ, соответству­ющего единичной дискрете входного сигнала, приложенной в мо­мент времени t=0 , в силу свойства линейности дискрете х[nТ] соответствует импульс

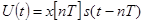(1)

(сдвиг аргумента t на nT объясняется тем, что импульс возникает при t=nТ и не раньше). Определим реакцию на дис­крету x[nT] последовательного соединения ИИЭ и непрерывного звена c импульсной переходной функцией s(t) (см. рис.6). При этом .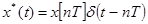

Пройдя через непрерывное звено, дельта-функция в силу свойств импульсной переходной характеристики развернется в сигнал 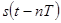и, таким образом, на выходе цепочки получим функцию 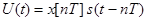, совпадающую с функцией (1) .Отсюда следует, что импульсный элемент с произвольной формой импуль­са s(t) можно представить как последовательное соединение ИИЭ и непрерывного звена с импульсной переходной функцией s(t). Это непрерывное звено может быть также задано своей передаточной функцией s(p)=L[s(t)]. Линейное звено, определяющее форму импуль­са, называют также формирующим звеном, или экстраполятором, и обычно присоединяют его к непрерывной части системы. Таким об­разом , в линейной импульсной системе с одним ИЭ можно выделить идеальный ИЭ и непрерывную часть.

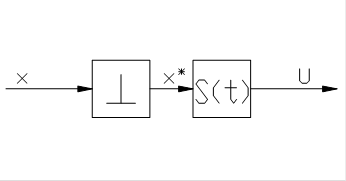Рис. 6