Задача о вершинном покрытии.
Определение 4.24. Множество вершин 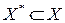 образует вершинное покрытие графа
образует вершинное покрытие графа 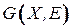 , если каждое ребро
, если каждое ребро 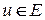 инцидентно хотя бы одной вершине из множества
инцидентно хотя бы одной вершине из множества 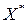 . Покрытие с минимальным числом вершин называется минимальным (оптимальным).
. Покрытие с минимальным числом вершин называется минимальным (оптимальным).
На рис. 4.5 множество вершин (3, 4) не образует покрытие, так как ни одно из ребер множества (1, 4) не инцидентно какой-либо из вершин множества (3, 4). Множество вершин (1, 3, 4) образует покрытие.
Сформулируем модель поиска минимального взвешенного покрытия графа в виде задачи целочисленного программирования. Введем 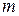 бинарных переменных:
бинарных переменных:

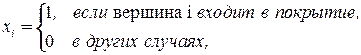
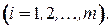
Тогда целевая функция имеет вид
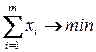 ,
,
условия инцидентности для всех ребер запишутся в виде
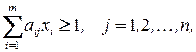
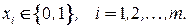
В задаче о взвешенном вершинном покрытии каждой вершине 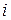 отнесен вес
отнесен вес 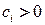 . В этом случае целевая функция имеет вид
. В этом случае целевая функция имеет вид
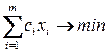 ,
,
ограничения – те же.
4.1.4. Задача об изоморфизме графов.
Рассмотрим графы 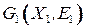 и
и 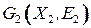 ;
; 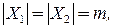
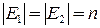 . Говорят, что эти графы изоморфны, если можно установить взаимно однозначное соответствие между их вершинами и ребрами так, что если вершины
. Говорят, что эти графы изоморфны, если можно установить взаимно однозначное соответствие между их вершинами и ребрами так, что если вершины 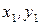 графа
графа 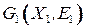 соответствуют вершинам
соответствуют вершинам 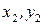 графа
графа 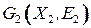 , то ребро
, то ребро 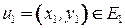 , если оно существует, соответствует ребру
, если оно существует, соответствует ребру 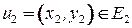 , если оно существует. Если ребро
, если оно существует. Если ребро 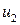 соответствует ребру
соответствует ребру 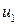 , то вершины
, то вершины 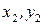 соответствуют вершинам
соответствуют вершинам 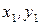 . Из данного определения следует, что изоморфные графы отличаются лишь нумерацией их вершин.
. Из данного определения следует, что изоморфные графы отличаются лишь нумерацией их вершин.
Рассмотрим простой пример (рис. 4.6). Способ перенумерации задается подстановкой
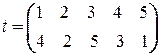 ,
,
причем в первой строке указаны вершины графа 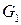 , а во второй ‑ соответствующие им вершины графа
, а во второй ‑ соответствующие им вершины графа 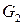 , при этом соответствие ребер имеет вид
, при этом соответствие ребер имеет вид
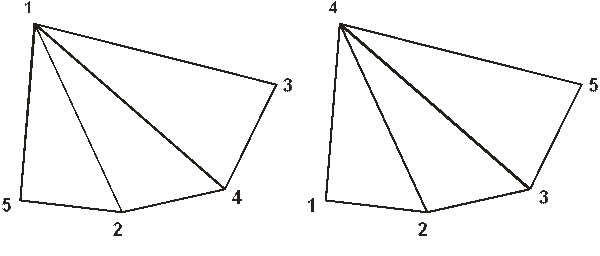
Рис. 4.6. Изоморфные графы.
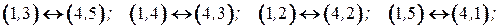
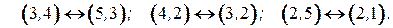
В общем случае для изоморфных графов требуется указать подстановку
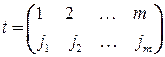 , (4.2)
, (4.2)
в которой вершине 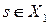 графа
графа 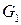 соответствует вершина
соответствует вершина 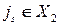 графа
графа 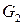 таким образом, чтобы выполнялось соответствие ребер.
таким образом, чтобы выполнялось соответствие ребер.
Сформулируем задачу об изоморфизме графов в терминах целочисленного программирования. Пусть 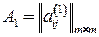 и
и 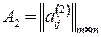 ‑ матрицы смежности графов
‑ матрицы смежности графов 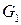 и
и 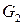 соответственно. Как известно [Kristof], для изоморфизма этих графов необходимо и достаточно существование такой невырожденной матрицы
соответственно. Как известно [Kristof], для изоморфизма этих графов необходимо и достаточно существование такой невырожденной матрицы 
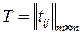 , имеющей одну единицу в каждой строке и каждом столбце, чтобы выполнялось условие
, имеющей одну единицу в каждой строке и каждом столбце, чтобы выполнялось условие
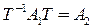 [7] (4.3)
[7] (4.3)
Условие (4.3) перепишем в виде
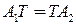 , (4.4)
, (4.4)
что равносильно следующим условиям:
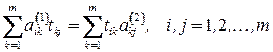 .
.
Задача о поиске матрицы 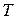 сводится к минимизации функции
сводится к минимизации функции
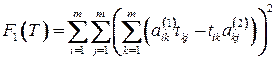
при условиях
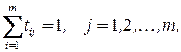
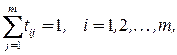
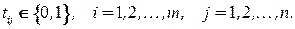
Если графы 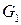 и
и 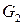 изоморфны, то минимальное значение функции
изоморфны, то минимальное значение функции 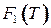 равно нулю и матрица
равно нулю и матрица 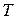 определяется через подстановку
определяется через подстановку 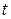 (4.2) следующим образом:
(4.2) следующим образом:
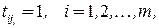
а все остальные ее элементы равны нулю. В нашем примере 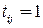 , если вершина
, если вершина 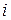 в графе
в графе 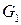 имеет номер
имеет номер 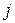 в графе
в графе 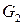 :
:
Рассмотрим другие целевые функции в задаче об изоморфизме графов:
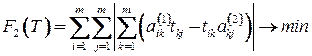 .
.
Эта целевая функция, в отличие от 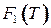 , не является дифференцируемой.
, не является дифференцируемой.
Обратим внимание на то, что каждая из сумм
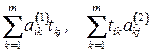 может принимать лишь значения 0 или 1. Поэтому сумма
может принимать лишь значения 0 или 1. Поэтому сумма 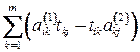 может принимать значения 0, 1, -1.
может принимать значения 0, 1, -1.
Целевую функцию 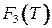 рассмотрим в виде
рассмотрим в виде
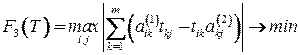 .
.
Очевидно, что 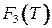 может лишь принимать значения 0 или 1.
может лишь принимать значения 0 или 1.
Нулевые минимальные значения нелинейных целевых функций 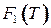 ,
, 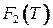 и
и 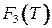 достигаются для изоморфных графов и только для них.
достигаются для изоморфных графов и только для них.
4.2. Экстремальные задачи на графовых структурах.
4.2.1. Задачи о раскрасках графов.
Задачи о раскрасках графов.
Задача о вершинной раскраске. Каждой вершине 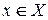 графа поставим в соответствие цвет
графа поставим в соответствие цвет 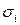 .
.
Определение 4.25. Вершинная раскраска графа называется правильной, если для любого ребра 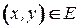 имеем
имеем 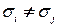 .
.
Правильно раскрашенный граф с некоторой фиксированной раскраской 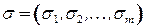 обозначим
обозначим 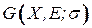 ;
; 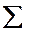 ‑ множество всех правильных раскрасок. Каждой правильной раскраске поставим в соответствие число цветов
‑ множество всех правильных раскрасок. Каждой правильной раскраске поставим в соответствие число цветов 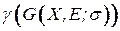 .
.
Определение 4.26. Хроматическим числом графа 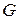 называется величина
называется величина
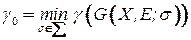 .
.
Хроматическому числу 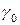 соответствует правильная раскраска
соответствует правильная раскраска 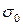 .
.
Немецкий математик Мёбиус (1790-1868) высказал в 1840 г. предположение, что для плоских графов 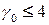 ; это предположение получило название гипотезы о четырех красках. Для плоских графов доказано, что
; это предположение получило название гипотезы о четырех красках. Для плоских графов доказано, что 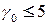 [8], для деревьев
[8], для деревьев 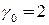 . Гипотеза о четырех красках в течение длительного времени оставалась недоказанной, она стала одной из самых знаменитых нерешенных задач математики. В 1976 г. эту гипотезу удалось доказать с применением компьютера. Было показано, что если
. Гипотеза о четырех красках в течение длительного времени оставалась недоказанной, она стала одной из самых знаменитых нерешенных задач математики. В 1976 г. эту гипотезу удалось доказать с применением компьютера. Было показано, что если 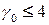 для некоторых специальных классов графов, то это условие выполняется для всех графов. Если же хотя бы для одного графа из этих специальных классов
для некоторых специальных классов графов, то это условие выполняется для всех графов. Если же хотя бы для одного графа из этих специальных классов 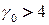 , то гипотеза неверна. Все эти специальные классы графов были проанализированы К. Аппелем и В. Хайкеном[9] на компьютере, для этого потребовалось около 2000 ч машинного времени одной из наиболее мощных ЭВМ того времени; гипотеза была подтверждена [6].
, то гипотеза неверна. Все эти специальные классы графов были проанализированы К. Аппелем и В. Хайкеном[9] на компьютере, для этого потребовалось около 2000 ч машинного времени одной из наиболее мощных ЭВМ того времени; гипотеза была подтверждена [6].
Сформулируем задачу о вершинной раскраске на языке целочисленного линейного программирования.
Пусть 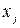 ‑ номер цвета, в который окрашена вершина
‑ номер цвета, в который окрашена вершина 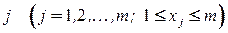 , такая раскраска является правильной, если, например,
, такая раскраска является правильной, если, например, 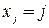 . Если
. Если 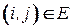 , то
, то 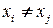 , что можно записать так:
, что можно записать так:
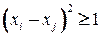 или
или 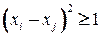 .
.
Целевая функция имеет вид
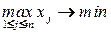 .
.
Итак, модель описывается соотношениями
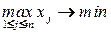
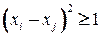 ,
, 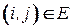 ,
,
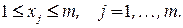
Построенная модель нелинейна по ограничениям и целевой функции. Поэтому рассмотрим другую модель. Введем бинарные переменные
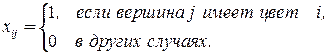
Каждая вершина имеет один цвет, что можно записать в виде
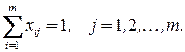
Если 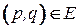 , то
, то
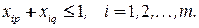
Если цвет с номером 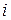 входит в раскраску, то
входит в раскраску, то
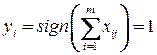 ,
,
если цвет 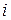 в раскраску не входит, то
в раскраску не входит, то 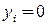 . Поэтому модель имеет вид
. Поэтому модель имеет вид
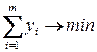 (4.5)
(4.5)
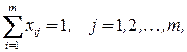 (4.6)
(4.6)
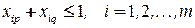 ,
, 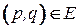 . (4.7)
. (4.7)
В самом деле, если ни одна из двух смежных вершин 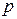 и
и 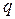 не окрашена в цвет
не окрашена в цвет 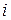 , то
, то
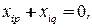
если одна из них (например, 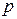 ) окрашена в цвет
) окрашена в цвет 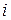 , то вторая из них (
, то вторая из них ( 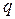 ) окрашена в другой цвет, поэтому
) окрашена в другой цвет, поэтому
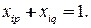
Итак, модель описывается соотношениями (4.5)-(4.7).
Дата добавления: 2016-06-05; просмотров: 2373;











