Задача о реберной раскраске.
Определение. Реберная раскраска называется правильной, если любые два смежных ребра имеют разные цвета. Реберная раскраска с минимальным числом цветов называется минимальной.
Из этого определения следует, что минимальное число цветов в правильной реберной раскраске оценивается снизу степенью графа, т.е. максимальной степенью вершин.
Минимальное число цветов 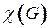 в правильной реберной раскраске называется хроматическим классом графа. Пусть
в правильной реберной раскраске называется хроматическим классом графа. Пусть 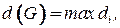
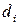 ‑ степень вершины
‑ степень вершины 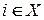 . Для графа без петель и кратных дуг верна оценка[10]
. Для графа без петель и кратных дуг верна оценка[10]
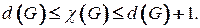
Сформулируем задачу поиска минимального числа цветов в реберной раскраске в терминах целочисленного программирования. Пусть 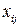 ‑ номер цвета, в который окрашено ребро
‑ номер цвета, в который окрашено ребро 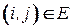 .
.
Тогда модель имеет вид:
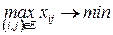 (4.8)
(4.8)
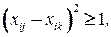
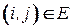 ,
, 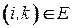 ,
, 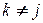 , (4.9)
, (4.9)
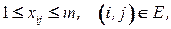 (4.10)
(4.10)
4.2.2. Построение остовного дерева минимального веса.
Минимальный остов
Задача о минимальном остове [6] состоит в отыскании остова минимального веса во взвешенном графе 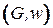 , где
, где 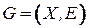 ‑ граф,
‑ граф, 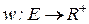 ‑ вещественнозначная функция, ставящая в соответствие каждому ребру
‑ вещественнозначная функция, ставящая в соответствие каждому ребру 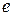 положительное (или неотрицательное) число
положительное (или неотрицательное) число 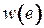 ‑ вес ребра
‑ вес ребра 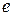 .
.
Задача о минимальном остове считается одной из самых «легких» оптимизационных задач па графах. Решение этой задачи можно получить с помощью «жадного» алгоритма, задав процедуру, которая по любому ациклическому множеству ребер 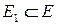 и ребру
и ребру 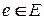 определяет, содержит ли множество ребер
определяет, содержит ли множество ребер 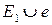 цикл графа
цикл графа 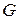 . В качестве такой процедуры можно использовать поиск в глубину, поскольку выявление цикла в множестве
. В качестве такой процедуры можно использовать поиск в глубину, поскольку выявление цикла в множестве 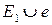 , где
, где 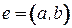 , равнозначно отысканию
, равнозначно отысканию 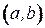 -цепи в порожденном подграфе
-цепи в порожденном подграфе 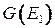 . В процессе работы «жадного» алгоритма эта процедура выполняется не более
. В процессе работы «жадного» алгоритма эта процедура выполняется не более 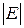 раз, и, следовательно, затраты времени составят
раз, и, следовательно, затраты времени составят 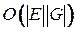 .
.
Для упорядочения множества 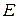 по неубыванию весов известны алгоритмы сложности
по неубыванию весов известны алгоритмы сложности 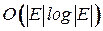 . Таким образом, даже использование «жадной» стратегии поиска минимального остова приводит (независимо от способа задания графа
. Таким образом, даже использование «жадной» стратегии поиска минимального остова приводит (независимо от способа задания графа 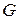 ) к полиномиальному алгоритму сложности
) к полиномиальному алгоритму сложности 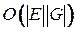 [11].
[11].
Рассмотрим алгоритм построения остовного дерева минимального веса, предложенный Примом [2, с. 73]. Алгоритм Прима порождает дерево посредством разрастания только одного поддерева, например 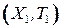 , содержащего более одной вершины. «Одиночные» вершины рассматриваются как отдельные поддеревья (т. е.
, содержащего более одной вершины. «Одиночные» вершины рассматриваются как отдельные поддеревья (т. е. 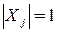 ,
, 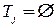 для всех
для всех 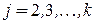 ). Поддерево
). Поддерево 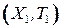 постепенно разрастается за счет присоединения ребер
постепенно разрастается за счет присоединения ребер 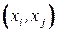 , где
, где 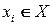 и
и 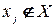 , причем добавляемое ребро имеет наименьший вес
, причем добавляемое ребро имеет наименьший вес 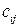 среди ребер из
среди ребер из 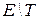 . Процесс продолжается до тех пор, пока число ребер в
. Процесс продолжается до тех пор, пока число ребер в 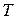 не станет равным
не станет равным 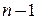 . Тогда дерево
. Тогда дерево 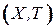 будет требуемым остовом графа
будет требуемым остовом графа 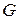 .
.
Алгоритм начинает работу с присвоения каждой вершине 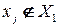 пометки
пометки 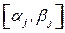 , где
, где 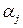 на каждом шаге есть ближайшая к
на каждом шаге есть ближайшая к 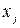 вершина из
вершина из 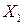 а
а 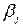 ‑ вес ребра
‑ вес ребра 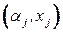 . На каждом шаге алгоритма вершина, например
. На каждом шаге алгоритма вершина, например 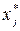 , с наименьшей пометкой
, с наименьшей пометкой 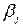 присоединяется к
присоединяется к 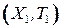 посредством добавления ребра
посредством добавления ребра 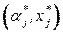 . Поскольку к
. Поскольку к 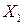 добавлена новая вершина
добавлена новая вершина 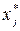 , то, может быть, придется изменить пометки у некоторых вершин
, то, может быть, придется изменить пометки у некоторых вершин 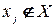 , и после этого продолжить процесс.
, и после этого продолжить процесс.
Алгоритм Прима имеет следующий вид.
Инициализация
Пусть 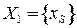 , где
, где 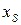 — произвольно выбранная вершина из
— произвольно выбранная вершина из 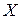 ,
, 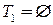 .
.
Основной цикл
Шаг 1. Для каждой вершины 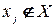 найти вершину
найти вершину 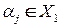 такую, что
такую, что 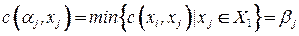 и приписать вершине
и приписать вершине 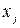 пометку
пометку 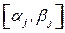 . Если такой вершины
. Если такой вершины 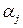 нет, т. е. при
нет, т. е. при 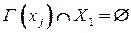 , приписать вершине
, приписать вершине 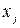 пометку
пометку 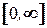 .
.
Шаг 2. Выбрать такую вершину 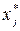 , что
, что 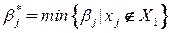 .
.
Обновить данные:
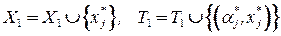 .
.
Если 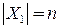 , то останов. Ребра в
, то останов. Ребра в 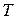 образуют остов минимального веса. Если
образуют остов минимального веса. Если 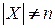 , то перейти к шагу 3.
, то перейти к шагу 3.
Шаг 3. Для всех 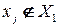 таких, что
таких, что 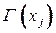 обновить пометки следующим образом:
обновить пометки следующим образом:
а) если 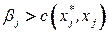 , то положить
, то положить 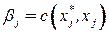 ,
, 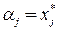 и вернуться к шагу 2;
и вернуться к шагу 2;
б) если 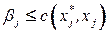 , то перейти к шагу 2.
, то перейти к шагу 2.
Вычислительная сложность алгоритма Прима составляет 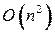 операций.
операций.
Для решения задачи построения остова минимального веса также используется алгоритм Краскала. Рассмотрим шаги этого алгоритма.
Инициализация
Положить 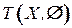 — несвязный граф, содержащий
— несвязный граф, содержащий 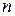 вершин.
вершин.
Сортировка
Упорядочить ребра графа 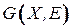 в порядке неубывания их весов.
в порядке неубывания их весов.
Основной цикл
Шаг 1. Начать с первого ребра в построенном на шаге Сортировка списке. Добавлять ребра графу 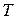 , соблюдая условие: добавление ребра не должно приводить к появлению цикла в
, соблюдая условие: добавление ребра не должно приводить к появлению цикла в 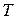 .
.
Шаг 2. Повторять шаг 1 до тех пор, пока число ребер в 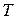 не станет равным
не станет равным 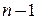 .
.
Дата добавления: 2016-06-05; просмотров: 2024;











