Графы как модели программ, данных и процессов
Управляющие графы. Многие задачи анализа программ, возникающие при их оптимизации, трансляции, проверке правильности, тестировании и т. д., значительно упрощаются, если их рассматривать на теоретико-графовых моделях. Базисной моделью является управляющий граф программы. Орграф G = (X, U) называется управляющим графом (р-графом, графом переходов), если выполнены следующие условия:
а) граф G не содержит параллельных дуг;
б) в множестве вершин графа выделена одна вершина S — вход графа;
в) в множестве верщин графа выделена хотя бы одна вершина 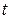 —выход графа;
—выход графа;
г) каждая вершина 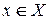 достижима из входа s;
достижима из входа s;
д) каждая вершина 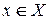 достигает выхода t.
достигает выхода t.
Замечание. Можно считать, что в управляющем графе имеется более чем один выход, поскольку этот случай легко сводится к случаю одного выхода введением фиктивного выхода, соединенного дугами с каждым фактическим выходом. В большинстве случаев можно считать, что полустепень исхода каждой вершины, отличной от входа и выхода, равна 1 или 2, а полустепень исхода входа равна 1.
Построение управляющего графа для конкретной программы производится по простым правилам с требуемой степенью детальности (и, как правило, автоматически). Тривиальное решение задачи состоит в изображении каждого оператора языка (команды, строки или любого фрагмента, признаваемого единицей языка) в виде отдельной вершины. При этом две вершины смежны, если между соответствующими операторами имеется передача управления. При этом оператор, после исполнения которого производится передача управления, представляется началом дуги; оператор, на который передается управление, ‑ концом дуги, а каждая передача управления ‑ дугой. При таком подходе размер графа сильно растет за счет появления длинных цепочек вершин, соответствующих линейным участкам программ. Они могут быть представлены одной вершиной.
Ордерево как форма организации динамических словарей. Пусть на вход некоторой программы подается некоторый текст и требуется составить список всех различных слов, встречающихся в тексте. Эта задача может быть усложнена требованием предоставления возможности пользоваться списком до включения в него всех слов. Кроме того, неизвестно обш;ее число слов в тексте. Для решения задачи с достаточной эффективностью требуется структура, которую можно было бы просмотреть за время, меньшее, чем потребовалось бы для неупорядоченного списка слов, и которая обладала бы еш;е одним свойством: вписывание новых слов не должно вызывать затруднений. Такой структурой служит корневое упорядоченное дерево в виде бинарного (или 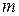 -арного) дерева сортировки — бинарного дерева, снабженного метками, взятыми из множества меток с введенным на нем отношением полной упорядоченности, и такого, что все метки из левого поддерева любой вершины меньше метки в этой вершине, а меток в правом поддереве — соответственно больше.
-арного) дерева сортировки — бинарного дерева, снабженного метками, взятыми из множества меток с введенным на нем отношением полной упорядоченности, и такого, что все метки из левого поддерева любой вершины меньше метки в этой вершине, а меток в правом поддереве — соответственно больше.
Включение нового слова соответствует подвешиванию к дереву новой вершины, меткой которой было бы новое слово, без нарушения свойства дерева быть бинарным. Для отыскания места подвешивания новой вершины будем двигаться, начиная с корня и сравнивая включаемое слово с метками проходимых вершин: если метка совпадает с включаемым словом, то ничего делать не надо, так как слово уже в словаре; если метка больше нового слова, то движемся к потомку вершины по левой дуге, в противном случае—по правой.
Если слова в словаре нет, то мы попадаем в вершину, у которой отсутствует один или оба потомка; к ней и подвешиваем новую вершину.
Граф-модель вычислительного процесса. Пусть дана некоторая формула, или задача, состоящая из ряда подзадач, или совокупность задач, использующих одни и те же ресурсы, и т. п. Для простоты будем говорить о вычислении некоторой формулы. Порядок вычислений может существенно влиять на объем требуемой для хранения исходных и промежуточных данных оперативной памяти. Изобразим формулу в виде каскадного информационного графа. В нем каждая внутренняя вершина соответствует оператору; это означает, что в эту вершину входит столько дуг, сколько аргументов у оператора, а выходит одна дуга, представляющая результат вычислений. Вводимым данным будут соответствовать вершины, из которых исходит только одна дуга и ни одна дуга не входит, ‑ входы графа.
Пример.Рассмотрим пример изображения формулы 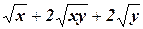 в виде ордерева.
в виде ордерева.
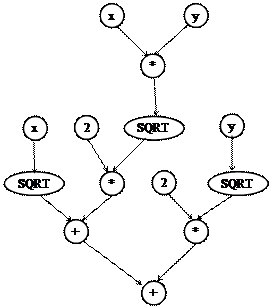 |
Отсюда следует, что каскадный информационный граф представляет собой корневое ордерево, в котором корень соответствует вычисляемому результату. В качестве веса вершины в такой модели вычислительного процесса выступает требуемый объем памяти.
Граф-модель информационно-логической системы. Среди исходных данных, необходимых для выбора структуры комплекса вычислительных средств (КВС), важнейшую роль играют сведения о множестве задач, решаемых системой. Простейшей формой задания такого множества является перечень задач; следующей по сложности формой является комплект алгоритмов решения задач системы. Наиболее развитой и совершенной формой задания вычислительной работы системы является информационно-логическая структура (ИЛС) системы, под которой понимается совокупность алгоритмов, увязанных в единое целое по перерабатываемой информации, для решения общей главной задачи системы.
Описание ИЛС системы должно включать в себя не только перечень алгоритмов, но и указания о последовательности их реализации, об их характеристиках и об исходной информации. Наиболее удобная форма описания ИЛС ‑ представление ее в виде орграфа алгоритмов.
Такие графы позволяют не только выявлять свойства ИЛС, но и решать следующие важные практические задачи:
— установление рационального порядка разработки алгоритмов;
— перечисление возможных вариантов привязки алгоритмов к пунктам обработки информации;
— составление исходных матриц, необходимых для оптимизации KBС по показателям качества КВС;
— упрощение ИЛС системы;
— составление управляющих (диспетчерских) алгоритмов.
Графом алгоритмов системы называется орграф 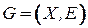 , вершины
, вершины 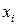 которого изображают частные реализации
которого изображают частные реализации 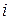 -х алгоритмов системы. Две вершины
-х алгоритмов системы. Две вершины 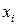 и
и 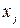 соединяются дугой
соединяются дугой 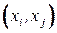 , если алгоритм
, если алгоритм 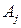 может реализоваться только вслед за алгоритмом
может реализоваться только вслед за алгоритмом 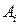 .
.
Вершинам графа алгоритмов приписывается вес, оценивающий реализацию этих алгоритмов, например число операций 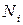 , требуемых для реализации
, требуемых для реализации 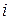 -го алгоритма, время
-го алгоритма, время 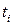 реализации алгоритма
реализации алгоритма 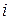 на компьютере, число ошибок определения тех или иных величин в результате реализации
на компьютере, число ошибок определения тех или иных величин в результате реализации 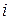 -го алгоритма и т. д.
-го алгоритма и т. д.
В ИЛС системы управления соотношения следования между алгоритмами обычно соответствуют направлениям потоков информации, которые циркулируют в системе при реализации алгоритмов. В самом деле, соотношение 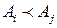 (алгоритм
(алгоритм 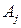 следует за
следует за 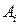 ) однозначно утверждает, что для реализации
) однозначно утверждает, что для реализации 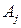 необходима некоторая входная информация, которая получается в результате реализации алгоритма
необходима некоторая входная информация, которая получается в результате реализации алгоритма 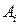 . Вследствие этого в графах алгоритмов не только вершинам, но и дугам могут быть приписаны вполне определенные веса, поскольку дуги описывают направленные потоки информации между последовательными алгоритмами, описываемые ее составом, объемом и точностными характеристиками. В некоторых случаях дугам графа приписана вероятность
. Вследствие этого в графах алгоритмов не только вершинам, но и дугам могут быть приписаны вполне определенные веса, поскольку дуги описывают направленные потоки информации между последовательными алгоритмами, описываемые ее составом, объемом и точностными характеристиками. В некоторых случаях дугам графа приписана вероятность 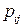 перехода от вершины
перехода от вершины 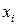 к вершине
к вершине 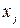 .
.
Дата добавления: 2016-06-05; просмотров: 2084;











