Основные определения теории графов.

Структура дискретных моделей описывается совокупностью бинарных отношений на наборах элементарных единиц данных и действий. Бинарные отношения описываются графами, которые являются фундаментальным понятием теоретической информатики.

Определение 4.1. Неориентированный граф 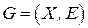состоит из конечного непустого множества 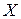вершин и множества 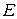неупорядоченных пар различных вершин 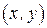, называемых ребрами.

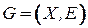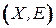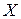Определение 4.2. Ориентированным графом называется упорядоченная пара , где есть непустое множество вершин орграфа, а 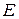есть множество упорядоченных пар элементов из 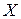, , 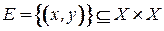называемых дугами орграфа.

Пусть 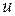‑ дуга орграфа вида 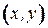, 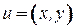. Вершина 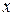называется началом дуги 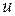, а вершина 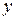‑ концом дуги 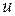. Прп этом говорят, что дуга 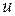выходит или исходит из вершины 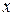и входит или заходит в вершину 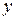, и в том, и в другом случае говорят, что дуга инцидентна соответствующей вершине. Дуга вида 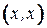называется петлей; вершины 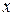и 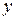, соединенные дугой, называются смежными.

Общее число дуг, инцидентных вершине 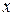, называется степенью вершины и обозначается .

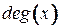Определение 4.3.Путем 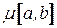из вершины 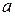в вершину 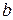называется последовательность вершин и дуг вида 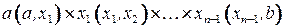. Путь называется простым, если ни одна вершина в нем не встречается дважды. Путь из входа 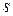орграфа в выход 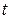называется 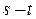-путем. Будем считать, что хотя бы один такой путь в орграфе существует. Если в орграфе вершины 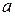и 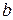связаны путем 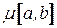, то говорят, что вершина 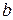достижима из вершины .

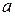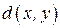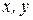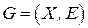Определение 4.4. Расстоянием между двумя различными вершинами графа называется длина кратчайшего пути, связывающего их.

Орграф называется односторонне связным, если для любой пары вершин одна достижима из другой. Орграф называется сильно связным, если для любой пары вершин каждая из них достижима из другой. Путь называется эйлеровым, если он содержит все дуги графа ровно по одному разу, и гамильтоновым, если он содержит все вершины ровно по одному разу.

Путь, начало и конец которого совпадают, т. е. путь вида 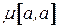, называется контуром (с начальной вершиной 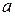). Контур называется простым, если ни одна вершина в нем не повторяется дважды, эйлеровым, если он содержит все дуги графа в точности по одному разу, и гамильтоновым, если он содержит все вершины графа в точности по одному разу. Длиной пути или контура называется число дуг, входящих в него.

Контур длины 1 есть петля. Путь длины 0 есть тривиальный или вырожденный путь. Длина эйлерова пути или контура равна числу дуг в орграфе; длина гамильтонова контура равна числу вершин в орграфе, длина гамильтонова пути на единицу меньше числа вершин.

Орграф 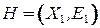называется частичным графом графа 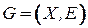, есл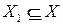и и 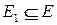, и суграфом, есл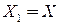и и 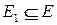. Орграф 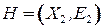называется подграфом графа 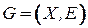, если 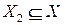и из того, что 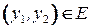и 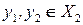, следует, что .

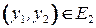Другими словами, частичный граф есть орграф, порождаемый некоторым подмножеством дуг исходного орграфа вместе с их концами. Суграф обязательно имеет то же мно;кество вершин, что и исходный (т. е. если порождающее множество дуг инцидентно не всем вершинам исходного графа, то частичный граф дополняется до суграфа за счет изолированных вершин).

Подграф порождается некоторым подмножеством вершин исходного графа и теми дугами, оба конца которых принадлежат указанному подмножеству.

Теорема 4.1. Для графа 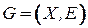следующие утверждения эквивалентны:

1) 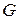‑ дерево;

2) любые две вершины в графе 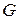соединены единственной простой цепью;

3) граф 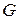связен и имеет 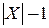ребер;

4) граф 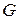не содержит циклов и имеет 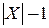ребер;

5) граф 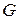не собержит циклов, но добавление ребра между двумя несмежными вершинами приводит к появлению одного цикла;

6) граф 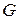связен, но утрачивает это свойство после удаления любого ребра.

Определим расстояние 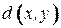между вершинам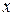и и 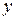в дереве как длину пути из 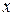в 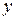. Расстояние от вершины 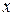до наиболее удаленной от нее вершины называется эксцентриситетом 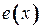вершины 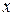, т. е. 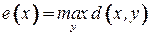. Наибольший из эксцентриситетов называется радиусом 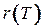дерева 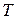. Центральной вершиной дерева 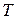называется вершина, у которой эксцентриситет равен радиусу. Центром дерева называется множество его центральных вершин.

Определение 4.5.Ориентированным корневым деревом 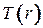или ордеревом с корнем 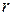называется орграф с выделенной вершиной 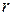, который удовлетворяет следующим условиям:

а) 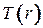‑ дерево (если не принимать во внимание ориентацию дуг;

б) из корня 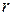достижима любая вершина (или корень 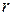достижим из любой вершины);

в) В корень 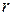не заходит ни одна дуга (или из корня не выходит ни одна дуга).

Важным типом упорядоченных деревьев являются так называемые бинарные деревья, определяемые рекурсивно следующим образом:

а) одновершинное дерево есть бинарное дерево;

б) тройка 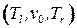есть бинарное дерево с корнем 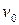, левым поддеревом 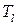и правым поддеревом 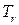, причем 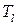и 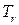‑ бинарные деревья (возможно, пустые); см. рис. 4.1.

Каркасом или остовом (стягивающим деревом) неориентированного графа называется его суграф в виде дерева. Граф 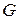имеет каркас тогда и только тогда, когда ои связен.

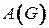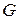Определение 4.6. Матрицей смежности графа с 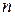вершинами называется квадратная матрица порядка 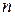с элементами 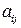: 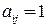, если существует дуга (ребро) 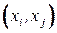; 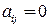в противном случае.

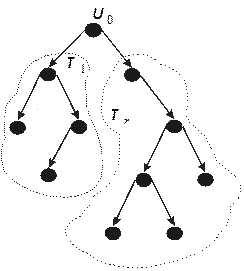
Рис. 4.1. Бинарные графы.

Для неориентированного графа матрица смежности симметрична относительно главной диагонали. В случае ориентированного графа входу соответствует столбец из нулей, выходу ‑ строка из нулей, число единиц в 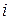-й строке равно полустепени исхода вершины 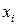, число единиц в 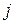-м столбце равно полустепени захода вершины .

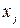Матрица смежности полностью определяет структуру графа (с точностью до изображения на плоскости и нумерации вершин), в том числе и взвешенного (в матрице смежности которого элемент 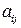равен весу дуги 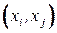). Пусть 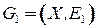, 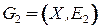‑ два графа с одним и тем же множеством вершин, 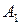и 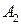‑ их матрицы смежности. Тогда матрица 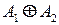, где символом 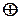обозначено логическое сложение, определяет объединение графов, т. е. граф .

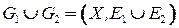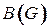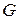Определение 4.7.Матрицей инцидентности графа с 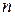вершинами и 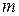дугами называется прямоугольная матрица размера 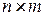с элементами 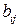: 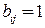, если вершина 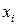есть начало дуги 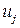; 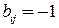, если вершина 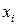есть конец дуги 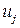; 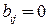в противном случае[1].

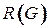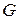Определение 4.8.Матрицей достижимости графа с 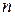вершинами называется квадратная матрица порядка 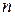с элементами 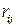: 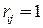, если вершина 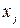достижима из 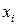, 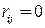в противном случае.

Определение 4.9. Клика ‑ подмножество вершин 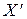графа 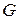, в котором любые две вершины смежны, т.е. порожденный им подграф 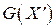является полным.

Определение 4.10. Транзитивное замыкание орграфа ‑ для данного орграфа 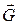орграф 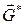с тем же множеством вершин, что и 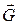, в котором дуга 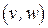существует тогда и только тогда, когда 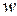достижима из 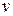в .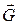

Определение 4.11. Транзитивная редукция орграфа ‑ для данного орграфа 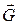орграф с наименьшим числом дуг, транзитивное замыкание которого совпадает (изоморфно) с транзитивным замыканием исходного графа .

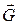Определение 4.12. Упорядочением 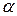вершин графа 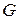называется биекция (взаимно-однозначное отношени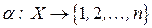е) , где .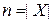

В дальнейшем будут использованы следующие стандартные обозначения теории графов [6]: 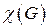‑ хроматическое число графа 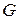, т.е. наименьшее число цветов, с помощью которых граф 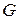может быть правильно раскрашен; 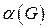‑ число независимости (число внутренней устойчивости), т.е. число вершин в наибольшем независимом множестве графа 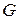; 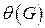‑ число кликового покрытия графа 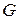, т.е. наименьшее число клик, покрывающих вершины графа; 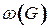‑ кликовое число, т.е. число вершин в наибольшей клике графа .

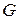Определение 4.13.Для заданного графа G = (V, E) древовидной деком­по­зицией (ДД) (tree decomposition) называется пара 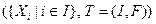, где 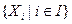‑ семейство подмножеств v и T ‑ дерево с множеством вершин i и множеством ребер 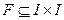такими, что

1) 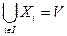; 2) для всех ребер 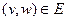существует 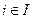такое, что 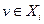и 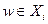; 3) для всех 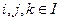таких, что j лежит на пути в T из i в k, справедливо включение .

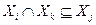ШиринойДД называется 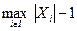. Древовидная ширина (ДШ) графа G опре­деляется как наименьшая ширина древовидной декомпозиции G и обо­значается tw(G). В частности, если в этом определении рассматривать не деревья, а пути (точнее, цепи), то получим определениепутевой ширины pw(G). Так как вся­кий путь есть дерево, то имеет место неравенство tw(G) ≤ pw(G). Графы с ДШ k известны также как частичные k –деревья.

Определение 4.14. Граф называется хордальным, если он не содержит ни одной порожденной клики C_k, k≥4.

Другими словами, в ХГ каждый цикл длиной ≥4 обладает хордой (т.е. реб­ром, соединяющем 2 несмежные вершины цикла). Полный граф K_n является, хордальным, а дву­дольный граф является хордальным тогда и только тогда, когда он ‑ лес. Хордальные графы[2] называются по-другому триангулированными графами или треугольными графами.

Определение 4.15.Триангуляцией графаG=(V,E) называется ХГ H=(V,F), содержащий G в качестве подграфа: .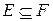

Определение 4.16.Вершина графа называется симплициальной, если она со своими соседями образует клику.

Определение 4.17. Граф G называется интервальным графом, если он является графом пересечений некоторого семейства замкнутых интервалов.

Определение 4.18. Для данного связного графа 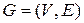множество вершин 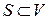называется сепаратором, если подграф 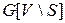графа 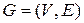несвязен.

Определение 4.19. Если 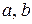‑ несмежные вершины связного графа 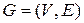, то множество вершин 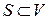называется 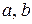-сепаратором, есл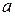и и 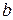находятся в разных компонентах связности подграфа .

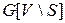Определение 4.20. 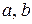-сепаратор 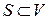называется минимальным, если ни одно собственное подмножество множества 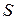не является 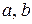-сепаратором.

Определение 4.21. 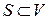‑ минимальный сепаратор графа 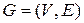, если найдутся вершины 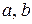графа 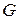, что 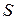является минимальным 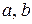-сепаратором.