Применение методов теории графов к организации вычислительного процесса

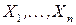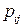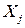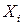Размещение блоков программы в оперативной памяти компьютера: сведение к задаче коммивояжера. Пусть ‑ отдельные блоки программы, и пусть ‑ вероятность исполнения блока после . Если 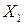‑ первый блок, а 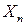‑ последний, то положим 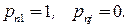Если марковский процесс, описываемый матрицей переходов 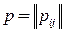, является эргодическим, т. е. для него существует предельное распределение, которое не зависит от начального состояния процесса, то частоты исполнения отдельных блоков 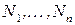удовлетворяют матричному уравнению 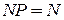, нормализованному так, что сумма частот исполнения равна 1. Пусть величины 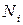найдены. Тогда, если 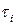‑ время исполнения блока 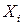, то ожидаемое время исполнения всей программы равно 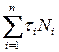. Есл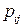и и 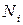известны, то можно рассмотреть задачу минимизации ожидаемого числа передач управления, производимых при выполнении программы. Если блок 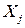следует в памяти за блоком 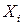, то передача управления нужна всякий раз, когда после блока 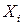выполняется блок 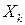, отличный от 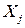. Ожидаемое число таких передач равно .

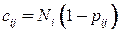Пусть 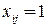, если блок 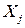непосредственно следует за блоком 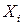в памяти, и 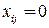в противном случае.

Пусть 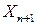‑ блок, состоящий из кодов начальных данных и кодов, которые не выполняются в виде команд. Тогда для всех 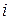имеем 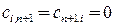. Полагаем 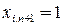, если 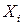‑ погледний блок в памяти, и 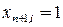, если 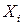— первый блок в памяти, в остальных случаях полагаем 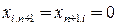, Тогда рассматриваемая задача сводится к минимизации ожидаемого числа выполнения передач управления 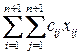при условии, что 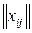есть матрица циклической перестановки, а это и есть задача коммивояжера (см. раздел 6.2.3).

Рассмотрим ситуацию, когда на входе компьютера ямеется некоторое множество задач, имеющих общие страницы в памяти. Требуется определить такую последовательность решения этих задач, чтобы минимизировать пересылки страниц памяти. Для решения построим граф, вершинам которого будут соответствовать задачи, а две вершины соединены ребром тогда и только тогда, когда они соответствуют задачам, имеющим общие страницы памяти. Каждому ребру сопоставляется вес, зависящий от числа общих страниц.

Тогда проблема активизации задач сводится к отысканию оптимального каркаса графа активизации. Особенность этой проблемы состоит в том, что чаще всего стоимость каркаса ‑ нелинейная функция от весов ребер.