Вершинная и дуговая совместимость

Вершинная совместимость состоит в рассмотрении каждой вершины графа ограничений и соответствующих ей унарных ограничений и выполне­нии сужения домена: если 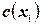‑ унарное ограничение для вершины 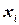, то­гда величины, не удовлетворяющие 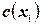, исключаются из домена 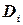. 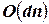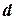Пря­мой алгоритм вершинной совместимости (node-consistency algorithm (NC)), удаляющий излишние элементы доменов переменных с помощью про­верки доменов одного за другим, имеет временную сложность , где ‑ максимальный размер доменов, а 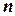‑ число переменных.

Дуговая совместимость состоит в рассмотрении каждой дуги, соответ­ствующей бинарному ограничению 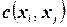, и выполнении сужения доменов. Величины, не удовлетворяющие 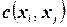, исключаются из доменов 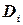и 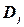. Можно определить 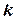-совместимость, рассматривая ограничения с 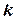перемен­ными (для 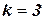‑ путевая совместимость, а 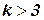‑ гипер-дуговая со­вместимость).

Проверку совместимости дуг можно использовать либо в качестве этапа предварительной обработки перед началом процесса поиска, либо в качестве этапа распространения ограничения (аналогично предварительной проверке) после каждого присваивания во время поиска.

Для данного ограничения говорят, что значение для переменной в огра­ничении имеет поддержку (support), если существуют такие значения для других переменных в этом ограничении, что это ограничение удовлетворя­ется.

Ограничение дуго-совместимо, если каждое значение из доменов пере­менных имеет поддержку.

Для достижения дуговой совместимости на 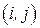, для каждого элемента 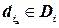, ищется элемент 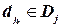, такой, что выполняется условие дуговой со­вместимости; 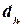поддерживает 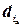. Все элементы домена без поддержки уда­ляются.

Удаление значений без поддержки часто называется усечением или суже­нием доменов.

Для ограничений, содержащих более двух переменных, дуговая совмес­тимость часто называется гипер-дуговой совместимостью или обобщенной дуговой совместимостью.

Например, рассмотрим ог­раничение 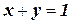с доменами переменных 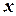и 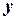‑ 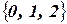. Вынуждение дуговой совместимости для этого ограниче­ния сужает домены обеих переменных до 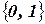. Величины, удаленные из доменов обеих переменных, локально несовместимы ‑ они не принадлежат ни одному набору присвоений переменных, удовлетворяющих ограничению, и поэтому не могут быть частью какого-либо решения всей за­дачи УО.

Для вынуждения дуговой совместимости в задаче УО требуется по­вторно удалять величины из доменов, пока не достигнем устойчивой точки. Оптимальный алгоритм для произвольного ограничения ха­рактеризуется временной сложностью в худшем случае, равной 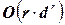, где 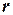‑ арность ограничения, а 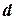‑ размер доменов переменных.

Простейшим методом достижения глобальной дуговой совместимости является повторение проходов по проверке каждой дуги задачи до тех пор, пока не будет никаких изменений графа ограничений после очередного про­хода. Этот подход реализован в виде алгоритма AC-1[10].

Вслед за исторически первым алгоритмом AC-1 были разработаны ал­горитмы AC-2,…, AC-7, каждый из которых улучшает хранение информации об измененных доменах и управление итерациями. Временная сложность ал­горитма AC-3 составляет 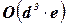, емкостная сложность ‑ 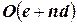, где 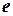‑ число бинарных ограничений. Алгоритм AC-4 улучшает AC-3 и имеет временную и емкостную сложность 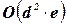. Другим усовершенствованием алгоритма AC-3 является алгоритм AC-5, исполь­зующий семантику специальных видов ограничений. Алгоритм AC-7 исполь­зует симметрию бинарных ограничений.

Определение 10.9. Задача УО является направленно-дуго-совместимой по отношению к упорядочению 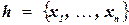, тогда и только тогда, когда каждая переменная 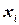реберно-совместима по отношению к каждой перемен­ной 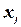, такой что .

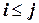Процедура распространения ограничений directional-arc-consistency работает с задачей УО 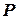(как обычно, задача УО ‑ это тройка 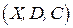( 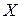‑ множество переменных, 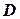‑ множество доменов и 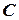‑ множество ограниче­ний) и упорядочением 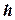для задачи УО. Процедура исследует переменные в обратном порядке 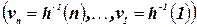. Для каждой переменной 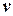она проверяет родителей 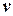или, иными словами, те переменные, соединенные с 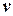, которые предшествуют 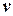в упорядочении; для задачи с шириной 1 число родителей будет всегда 0 или 1. Затем вызывается процедура Update-Domain для удале­ния из домена родителя всех значений, не совместных по крайней мере с од­ним значением из домена .

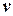Это ‑ законное преобразование, так как удаленное значение не является частью решения.

После выполнения этой предварительной обработки выясняется на­правленная дуговая совместимость. Это означает, что для любого значения домена переменной и для лю­бого сына этой переменной найдется по крайней мере одно значение из до­мена сына, совместимое со значением родителя.

Глобально совместимые ЗУО обладают свойством, что любое совмес­тимое присвоение значений подмножеству переменных может быть расши­рено до совместимого присвоения значений всем переменным без получения тупиков.