Путевая совместимость

Для бинарных задач УО имеется еще один вид совместимости ‑ путевая совместимость.

Определение 10.10. Бинарная задача УО является путе-совместимой (path-consistent), если для любого пути в ее графе ограничений справедливо сле­дующее: если присвоения значений начальной и конечной переменной пути совместимы, то это может быть расширено на совместимое частичное при­своение значений оставшимся переменных на пути.

Аналогично семейству алгоритмов дуговой совместимости, имеется се­мейство алгоритмов достижения путевой совместимости бинарной задачи УО. Эти алгоритмы также гарантируют вершинную и дуговую совмести­мость. Наилучший из этих алгоритмов ‑ PC-4, аналогичный AC-4, характери­зуется временной и емкостной сложностью вида .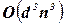

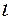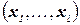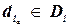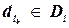Локальная путевая совместимость выполняется, если для данного пути длины через вершины , для всех значений и таких, что ограничения 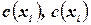и 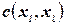выполняются, имеется последовательность значений: 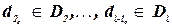, такая, что ограничения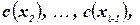 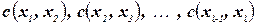выполняются. На рис. 10.7 показан пример для пути .

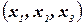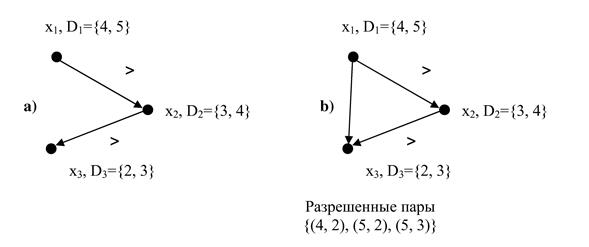
Рис. 10.7. Эффект вынуждения путевой совместимости.

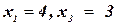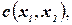
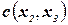Начальное состояние показано на рис. 10.7 a. Добавлено новое ограни­чение (рис. 10.7 b), которое не разрешает пару присвоений , т.к. для этих присвоений не существует присвоения для , удовлетворяющего . Вынуждение дуговой совместимости не разрешает этой пары присвоений.

Глобальная путевая совместимость выполняется, если любая пара при­своений значений, которые совместимы с прямым ограничением между двумя переменными, также совместима со всеми путями между двумя вер­шинами. Если любой путь длины 2 в полном графе ограничений является путе-совместимым, то путевая совместимость выполняется глобально.

Путевая совместимость вынуждается с помощью изменения прямого ограничения между начальной и конечной точкой пути для того, чтобы за­претить все пары назначений, которые нарушают требуемое условие. Истин­ные ограничения могут быть обновлены, добавляя новое явное ограничение к задаче (см. рис. 10.7).

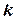-совместимость

Дуговая совместимость может также пониматься как информация о том, насколько далеко частичное решение может всегда быть расширено. А именно, любое частичное решение, содержащее лишь одну зафиксированную переменную, может быть расширено с помощью фиксации любой другой пе­ременной на соответствующим образом выбранном значении.

Применение того же принципа для большего числа переменных приво­дит к понятию 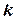-совместимости.

Определение 10.11 ( 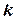-совместимость). Задача УО 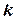-совместима, если лю­бой совместимый кортеж значений любых 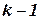переменных может быть рас­ширен путем задания значения любой одной из оставшихся переменных.

Задача УО строго 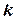-совместима тогда и только тогда, когда она 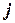-со­вместима для всех .

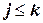Строго 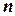-совместимая сеть, где 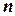‑ число переменных ЗУО, называется глобально совместимой.

Дуговая и путевая совместимость соответствуют 2- и 3-совместимости.

Заметим, что 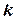-совместимая ЗУО не обязательно разрешима, и наобо­рот, разрешимость задачи не влечет за собой совместимости любого уровня, а не только 1-совместимость.