Логическое программирование в ограничениях

За последние 20 лет программирование в ограничениях прошло путь от научной идеи до мощной парадигмы про­граммирования, которая все больше используется для моделирования и ре­шения многих трудных практически важных задач.

Под программированием в ограничениях (constraint programming) по­нимается программирование алгоритмов решения задач УО. Программирование в ограничениях, считающееся в настоящее время одним из стратегических направлений информатики[20], является декла­ративной парадигмой, позволяющей выра­зить многие прикладные задачи с помощью ограничений. Программирование в ограничениях состоит из двух необходимых компонентов: решателя ог­раничений и машины поиска.

Логическое программирование ‑ это парадигма программирования, ос­нованная на логике. Его конструкты ‑ булевы импликации (т.е. 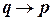или p:-q), композиций, использующих булевы операции конъюнкции и дизъюнкции. Логическое программирование может рассматриваться как процедурный язык, в котором процедуры ‑ это булевы функции, результат работы программы всегда истина или ложь.

Тот факт, что системы удовлетворения ограничений и логического про­граммирования ‑ декларативные парадигмы, использующие отно­шения и поиск с возвратами, сделал их интеграцию легкой и естественной. Логическое программирование в ограничениях ‑ расширение логиче­ского программиро­вания, в котором унификация может быть заменена или допол­нена другими видами ограничений, определенных на доменах (областях оп­ределения) ис­пользуемых переменных. Схема логического программирова­ния в ограниче­ниях (ЛПО) может рассматриваться как оболочка логического програм­миро­вания, поддерживае­мая системой ограничений, с помощью которой мо­жет записывать и решать любые ограничения. По этой причине схема ЛПО может обозначаться как ЛПО(X), где X определяет класс исполь­зуемых ограниче­ний.

Поскольку описание задачи в виде системы ограничений является декларативным, то при этом описывается, «что» должно выполняться, но не ука­зывается, «как» это сделать.

Общепринятый подход к решению задач УО сочетает дерево поиска с возвратами с распространением ограничений. Это реализовано в системах программирования в ограничениях с конечными доменами, таких как SICStus Prolog, ILOG Solver, и Gecode.