Метод множеств разрыва цикла

Метод множеств разрыва цикла (cycle cutset)[11] основан на том, что присвоение значения переменной устра­няет ее из дальнейшего рассмотрения в соответствующей ветви дерева поиска. Это сильно меняет топологию и связность оставшейся части графа ограничений.

Множество разрыва цикла графа ограничений – это множество вер­шин, при исключении которых (с помощью фиксациии соответствующих пе­ременных) остается дерево.

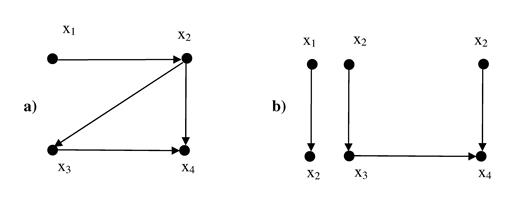
Рис. 10.8. Эффект фиксации множества разрыва цикла.

Рассмотрим пример на рис. 10.8 a). Фиксирование значения перемен­ной «блокирует» путь, проходящий через эту вершину, так что имеется только один путь между любыми двумя переменными (вершинами). В ре­зультате получается граф ограничений (рис. 10.8 b)), в котором зафиксиро­ванная сейчас переменная повторяется для каждой смежной переменной. Если множество фиксированных переменных совпадает с множеством раз­рыва цикла, то оставшийся граф имеет древовидную структуру и соответст­вующая ему задача может быть решена очень эффективно. Этот метод нахо­дит локально совместимое присвоение для переменных из множества разрыва цикла и решает оставшуюся (древовидную) задачу.

Если не найдено ни одного решения для данного присвоения значений переменным из множества разрыва цикла, то должно быть найдено другое совместимое присвоение для переменных из множества разрыва цикла и де­лается попытка решения задачи, соответствующей оставшейся части графа.

Нахождение минимального множества разрыва цикла является NP-пол­ной задачей. В связи с этим, целесообразно встраивать метод множества раз­рыва цикла в метод дерева поиска, такой, как поиск с возвратами. В случае, когда множество зафиксированных переменных образует множество разрыва цикла, оставшаяся часть задачи может быть быстро решена. По сравнению с поиском с возвратами на случайно сгенерированных задачах, метод поиска с возвратами, использующий множества разрыва цикла, в среднем на 20% эф­фективнее. По сравнению с наивной версией алгоритма обратного перехода, его комбинация с множествами разрыва цикла в среднем на 25% эффектив­нее.

Общий алгоритм решения указанным способом описан ниже.

· Выбрать подмножество 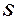из множества переменных ЗУО, такое, что граф ограничений после удаления 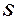становится деревом. Подмножество 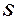называется множеством разрыва цикла.

· Для каждого возможного присваивания переменным в 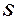, которое удовлетворяет всем ограничениям в 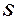, выполнить следующее:

ü удалить из областей определения оставшихся переменных любые значения, несовместимые с данным присваиванием для ;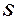

ü если оставшаяся задача УО имеет решение, вернуть это решение вместе с присваиванием для .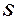

Если множество разрыва цикла имеет размер 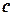, то общее время про­гона алгоритма составляет . В том случае, если граф по своей форме «очень близок к дереву», то множество будет небольшим, а экономия времени по сравнению с прямым поиском с возвратами окажется огромной. Но в наихудшем случае количество элементов 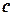может достигать 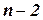. За­дача поиска наименьшего множества разрыва цикла является NP-трудной, но известно несколько эффективных алгоритмов решения этой задачи. В целом данный алгоритмический подход носит название определения условий выбора множества разрыва цикла (cutset conditioning).

Связные компоненты

Выделение связных компонентов графа может быть полезно при решении задач УО. Точка сочленения 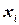в графе ограничений ‑ эта такая вершина, что все пути между дальнейшими вершинами должны проходить через нее. Раздели­мый граф содержит точку сочленения, а связный граф ‑ нет. Связный компо­нент ‑ это подграф без точек сочленения.

Even предложил алгоритм со сложностью для нахождения всех связных компонентов и точек сочленения[12].

На следующем шаге, после нахождения всех связных компонентов, не­обходимо найти все возможные решения для каждого из них. Решение всей задачи УО может быть получено с помощью склеивания решений для компо­нентов (с учетом совместимости значения для точки сочленения смежных компонентов).

Dechter & Pearl[13] предложили алгоритм со сложностью 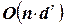, использующий описанный подход, где 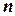‑ число переменных, а 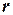‑ размер наибольшего компонента.