Распространение ограничений

Имеются различные виды методов для преодоления присущей задачам УО трудной разрешимости, в том числе распространение ограничений, называемое также сужением, с помощью которого исключаются значения. Распространение ограничений позволяет удалить избыточные значения из доменов переменных, что снижает размер пространства решений.

Распространение ограничений является центральным моментом в про­цессе решения задачи УО.

Уменьшение задачи может быть выполнено либо однократно ‑ в качестве этапа препроцессинга перед использованием какого-либо другого алгоритма, либо ‑ многократно, шаг за шагом, перемежаясь с исследованием пространства решений с помощью ал­горитма поиска. В последнем случае отсекаются подмножества пространства решений, экономя время, которое алгоритм поиска затратил бы на системати­ческое исследование отброшенных элементов. Если в результате уменьшения пространства решений какой-либо домен стал пустым, тогда отсюда следует, что рассматриваемая задача УО не имеет решений.

Распро­странение ограничений ‑ очень общее понятие, которое появляется под раз­ными названиями в зависимости от времени и авторов[9]. Ниже будут рассмотрены наиболее хорошо известные и используемые алгоритмы.

Препроцессинг или предварительная обработка в задачах УО создает эквивалентную, с тем же множеством решений, но более простую задачу, в результате чего по­иск на дереве может решить полученную задачу с гораздо меньшими затра­тами. Исходная задача УО преобразуется следующим образом. Вначале до­мены переменных могут фильтроваться для удаления элементов, которые не могут быть частью ни одного решения. Далее может быть изменено множество ограничений с целью недопущения несовместимых комбинаций присвое­ний, причем эти изменения производятся с помощью распространения ограничений: ис­пользуется локальная группа ограничений для получения информации, которая запоминается в виде измененного ограничения или уменьшенного домена переменной. Это локальное изменение является основой для получения дальнейшей информации, поэтому результат любого изменения постепенно распространяется по всей задаче.

Хотя с целью простоты изложения представленные здесь методы опи­саны для бинарных задач УО, они применимы к 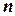-арной задаче УО (напри­мер, используя двойственную графовую интерпретацию).