Древовидная декомпозиция

Древовидная декомпозиция или кластеризация (Tree-clustering) (Dechter & Pearl[14]) преобразует произвольную 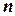-арную задачу УО в ациклическую форму в представлении в виде двойственного графа путем формирования кластеров из переменных, граф взаимосвязей которых имеет структуру де­рева. 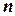-арная задача УО называется ациклической, если ее первичный граф ограничений обладает следующими свой­ствами:

· хордальность: каждый цикл, содержащий не менее 4 вершин, со­держит хорду (ребро, соединяющее 2 непоследовательные вершины цикла).

· конформность: каждая из максимальных клик графа соответст­вует одному ограничению в задаче УО.

Алгоритм триангуляции (Tarjan & Yannakakis[15]) может быть ис­пользован для достижения указанных свойств, используя два шага: a) Найти упорядочение с максимальной степенью (maximum cardinality) и б) рекур­сивно добавить ребра между вершинами, соединяющими вершины, с боль­шим порядком согласно указанному упорядочению. На рисунках 10.12 a и b (из (Dechter & Pearl[16])) соответственно показаны первичный граф ограничений задачи УО до и после процесса триангуляции.

Максимальными кликами этого графа являются кластеры, которые со­ставляют ограничения преобразованной задачи УО (см. рис. 10.10 a).

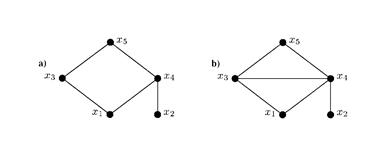
Рис. 10.9. Построение хордального первичного графа.

Для построения дерева из этого представления достаточно удалить лишние ребра из графа, т.е. те ребра, удаление которых не оказывает влияния на множество решений.

В двойственном графе дуга избыточна, если множество переменных, которым она помечена, является общим для всех дуг на отдельном пути ме­жду конечными вершинами дуги.

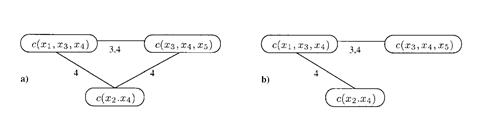
Рис. 10.10. Построение дерева из двойственного графа.

На рис. 10.10 b) показан один способ построения дерева для задачи УО.

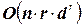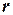Сложность этой процедуры , где ‑ размер наибольшей макси­мальной клики.

Понятие ширины дерева ввели в теории графов Робертсон и Сеймур (Robertson & Seymour, 1986)[17]. (Dechter & Pearl, 1987, 1989) применяли то же понятие (названное ими индуцированной шириной) к задачам УО и разработали подход, использую­щий древовидную декомпозицию (tree decomposition) (см. тему 8) графа огра­ничений и создании множества связанных подзадач. Каждая подзадача реша­ется независимо, а затем итоговые решения комбинируются. Этот алгоритм работает успешно, если подзадачи не слишком велики. Любая древовидная декомпозиция должна удовлетворять трем приведенным ниже требованиям.

1) Каждая переменная из первоначальной задачи появляется по мень­шей мере в одной из подзадач.

2) Если две переменные первоначальной задачи связаны ограниче­нием, то должны появиться вместе (наряду с этим ограничением) по меньшей мере в одной из подзадач.

3) Если какая-то переменная появляется в двух подзадачах в дереве, то должна появляться в каждой подзадаче вдоль пути, соединяющего эти под­задачи.

Первые два условия гарантируют, что в декомпозиции будут представ­лены все переменные и ограничения. Третье условие просто отражает то ог­раничение, что любая конкретная переменная должна иметь одно и то же зна­чение в каждой подзадаче, в которой появляется; соблюдение этого ограни­чения гарантируют связи, соединяющие подзадачи в дереве.

Каждая подзадача решается независимо; если какая-либо из них не имеет решения, то вся задача также не имеет решения. После решения всех подзадач составляется решение исходной задачи путем решения задачи с ог­раничениями, связывающими подзадачи; для этого используется эффектив­ный алгоритм для деревьев. Ограничения, связывающие подзадачи, указы­вают на то, что решения подзадач должны быть согласованными по их общим переменным. Любой конкретный граф ограничений допускает большое коли­чество древовидных декомпозиций; при выборе декомпозиции нужно стре­миться к тому, чтобы подзадачи были как можно меньше. Ширина дерева древовидной декомпозиции графа на единицу меньше размера наибольшей подзадачи; ширина дерева самого графа определяется как минимальная ши­рина дерева среди всех его древовидных декомпозиций. Если граф имеет ши­рину дерева 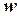и дана соответствующая древовидная декомпозиция, то соответ­ствующая задача может быть решена за время 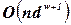. Это означает, что задачи УО с графами ограничений, характеризующимися конечной шири­ной дерева, могут быть решены за полиномиальное время. К сожалению, за­дача поиска декомпозиции с минимальной шириной дерева является NP-трудной, но существуют эвристические методы, которые хорошо работают на практике.