Бинарные и общие задачи удовлетворения ограничений

В данном разделе рассматриваются задачи УО с дискретными перемен­ными. Задачи УО простейшего вида характеризуются тем, что в них исполь­зуются дискретные переменные, которые имеют конечные домены[4] (области определения). К такому виду относится задача раскраски карты. Описанная выше задача с восемью ферзями также может рассматриваться как задача УО с конечной областью определения, где переменные 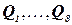представляют собой позиции каждого ферзя на столбцах 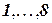, а каждая переменная имеет область определения .

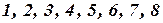Если максимальный размер доменов переменных в задаче УО равен 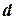, то количество возможных полных присваиваний значений 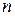переменным изме­ряется величиной 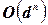, т.е. зависит экспоненциально от количества перемен­ных. К классу задач УО с конечной областью определения относятся булевы задачи УО, в которых переменные могут иметь значения либо истина, либо ложь. Булевы задачи УО включают в качестве частных случаев некото­рые NP-полные задачи, такие как задача выполнимости 3SAT.

Дискретные переменные могут иметь бесконечные области определе­ния, например, такие, как множество всех целых чисел. В частности, при ка­лендарном планировании строительных работ дата начала каждой работы представляет собой переменную, а ее возможными значениями являются це­лочисленные интервалы времени в сутках, отсчитываемые от текущей даты. При решении задач с бесконечными областями определения невозможно опи­сывать ограничения, перечисляя все допустимые комбинации значений. Вме­сто этого должен использоваться специальный язык ограничений. Например, если работа 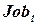которая занимает пять дней, должна предшествовать работе 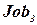, то для описания этого условия потребуется язык ограничений, представ­ляющий эти условия в виде 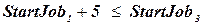. Кроме того, невозможно решать такие ограничения, просто перечисляя все воз­можные присваивания, поскольку количество подобных возможных присваи­ваний бесконечно велико. Для линейных ограничений с целочисленными пе­ременными существуют специальные алгоритмы поиска решений.

Сеть ограничений или задача удовлетворения ограничений (УО) со­стоит из множества переменных 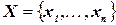, множества доменов значений 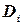для каждой переменной 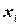, и множества ограничений и отношений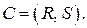

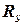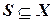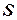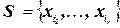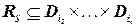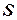Каждый домен значений является конечным множеством значений, ко­торые может принимать сответствующая переменная. Ограничение над ‑ это подмножество декартова произведения доменов переменных в . Если , то . называется диапазоном (scope) ограничения .

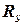В бинарной сети ограничений все ограничения заданы над парами пе­ременных. Граф ограничений ставит в соответствие каждой переменной вер­шину, причем две вершины соединяются ребром, если соответствующие пе­ременные имеются в диапазоне какого-либо ограничения.

При задании ограничений используются отношения.

Определение 10.1.Для данных множества переменных 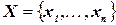и соот­ветствующих их областей значений 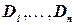отношением 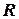на множе­стве переменных называется любое подмножество декартова произведения их областей значений. Множество переменных, на котором определено отноше­ние 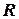, называется диапазоном отношения и обозначается .

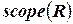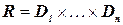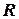Если , то называется универсальным отношением. От­ношения могут задаваться с помощью таблиц, описывающих допустимые со­четания значений переменных.

Определение 10.2. Задача УО (ЗУО) определяется множеством дискретных переменных 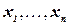, для каждой из которых задана область определения или домен 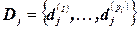, , 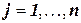и множеством ограничений. Ограниче­нием называется пара 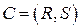, где 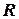‑ отношение, определенное на диапазоне 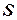. Решением ЗУО называется присвоение значений всем перемен­ным, которое удовлетворяет всем ограничениям. Целью решения ЗУО может быть нахождение одного или всех решений.