Графовые представления структуры задачи удовлетворения ограничений

Структура или топология задач УО может описываться с помощью раз­личных графовых структур: (первичного) графа ограничений, гиперграфа ог­раничений, двойственного графа ограничений.

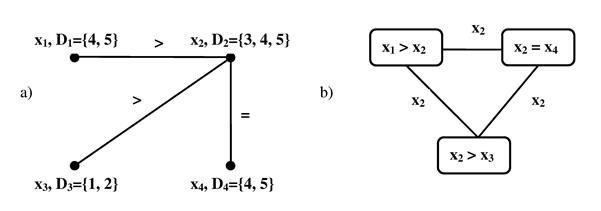
Рис. 10.4. a) Граф ограничений и b) двойственный граф.

Определение 10.3. Первичный граф ограничений ЗУО 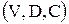‑ это неориен­тированный граф 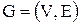, вершины 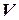которого соответствуют переменным ЗУО, причем две вершины соединяются ребром в графе 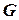, если соответствующие переменные имеются в одном и том же ограничении (т.е. в одном и том же диапазоне какого-то отношения).

Граф ограничений определен как для бинарных, так и для небинарных ограничений. Однако для небинарного случая структура ограничений может быть более точно передана с помощью гиперграфа ограничений.

Гиперграф ограничений ЗУО ‑ это гиперграф 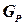, вершины которого соот­ветствуют переменным задачи УО, а гиперребра ‑ ограничениям 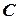, вер­нее, подмножествам переменных из диапазонов ограничений .

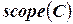Гиперграф, соответствующий бинарной ЗУО, является обычным графом. Гиперграф, соответствующий небинарной ЗУО, может быть преобразован к обычному графу ограничений путем замены каждого гипер­ребра кликой, состоящей из вершин гиперграфа и соединяющих их ребер.

В ряде случаев удобно использовать двойственный граф ограничений (см. рис. 8.5), вершины которого соответствуют диапазонам ограничений, а ребра соеди­няют вершины при наличии в них общих переменных. При этом ребра поме­чаются множествами общих переменных. Заметим, что двойственный граф ограничений тесно связан с двойственной ЗУО, в которой переменными (так называемыми c-переменными) являются ограничения исходной задачи. Огра­ничения двойственной задачи вынуждают общие переменные из ограничений принимать одни и те же значения, т.е. двойственные ограничения бинарны. Отсюда видно, что с помощью двойственных задач УО можно любую неби­нарную ЗУО свести к бинарной и решить ее с помощью методов решения би­нарных УО.