Методы поиска с возвратами

Возможно сформулировать задачи УО в виде задач поиска, что позво­ляет решать задачи УО с помощью алгоритмов поиска. Поиск с возвратами, описанный в главах 4 и 6, может использоваться для задач удовлетворения ограничений[8].

Нвпомним, что поиск в глубину, в котором каждый раз выбираются значения для од­ной переменной и выполняется возврат, если больше не остается допустимых значений, которые можно было бы присвоить переменной, называется поис­ком с возвратами (backtracking).

Дерево присвоений значений переменным ‑ это дерево, в котором каж­дая вершина соответствует множеству присвоений, причем корень дерева отвечает пустому множеству присвоений. В каждой вершине 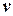выбирается перемен­ная, которой в 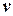не было присвоено значение. Алгоритмы поиска с возвра­тами выполняют поиск в глубину в этих деревьях присвоений значений.

Алгоритмы поиска с возвратами ‑ это алгоритмы систематического по­иска для задач УО, которые используют частичные присвоения, и строят частичное решение путем поочередного присваи­вания значений переменным. Если алгоритм обнаруживает тупик, в котором частичное решение не имеет совместимого расширения, то выбор последнего присвоения отменяется и делается попытка присвоения другого значения. Этот процесс повторяется до тех пор, пока не будут исчерпаны все возможно­сти и/или не будет найдено решение.

Алгоритмы поиска с возвратами являются полными в том смысле, что они находят решение, если оно существует.

Алгоритм поиска с возвратами характеризуется экспоненциальной вре­менной сложностью, но является линейным по используемой памяти.

Простейшим методом решения задач УО является метод ''Generate and Test'', который порождает каждое возможное решение (путем присвоения всех возможных значений для каждой переменной) и проверяется, удовлетво­ряет ли оно всем ограничениям. В наихудшем случае число всех возможных проверенных решений равно размеру декартова произведения доменов всех переменных (см. 6.1.1), в связи с чем метод полного перебора может требовать больших затрат времени при решении задач.

Хронологический поиск с возвратами (chronological backtracking) усо­вершенствует схему ''Generate and Test'', рассматривая процесса поиска как постепен­ное расширение частичных решений. Порядок задания значений ‑ это поря­док, в котором присваиваются значения переменным во время поиска. На уровне 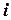порядка присваивания прошлые (т.е. ранее рассмотренные) переменные имеют индексы, мень­шие чем 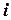, причем им уже присвоены значения. Будущие переменные имеют ин­дексы, большие, чем 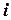, и им еще не присвоены значения.

На рис. 10.5 на псевдокоде описан алгоритм поиска с возвратами для случая бинарных ограничений. Для простоты, псевдокод не различает случаев, когда не найдено решений или когда не найдено больше решений, возвращается значение ложь в обоих слу­чаях.

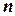В описании алгоритма используются следующие обозначения: ‑ число переменных задачи; Assignments [i] ‑ массив размерности 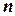запоминает значение, присвоенное в настоящий момент каждой переменной 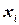; 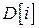содержит последовательность элементов домена, соответствую­щего переменной .

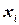Рис. 10.5. Поиск с возвратами.

Функция 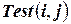возвращает значение истина, если бинарное ограничение 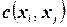удовлетво­ряется текущими присвоениями значений переменным 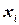и 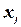. Если 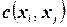не существует, Test( ) возвращает истина (это не считается про­веркой ограничения). Каждый элемент домена 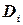поочередно присваива­ется переменной 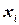, расширяя тем самым текущее присвоение переменным 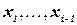. Если про­верка ограничения для предыдущей переменной не проходит, это частичное присвоение больше не расширяется. Если домен 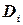исчерпан (тупик или пол­ное исчерпание домена), алгоритм делает возврат до уровня 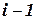с целью нахождения другого совместимого присвоения для 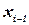. Если такого нет, он делает возврат к 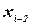, и т.д. пока не будет найдена переменная с другим совмес­тимым присвоением или будет показано, что ЗУО не имеет решения.

Для данного совместимого присвоения (все проверки ограничений были успешны), делается рекурсивный вызов BT 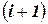или, если не остается свободных переменных, получено решение.

Поиск с возвратами может рассматриваться как обход вершин дерева.

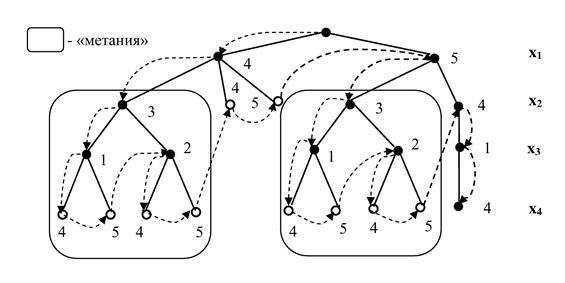
Рис. 10.6. Поиск с возвратами как обход дерева.

На рис. 10.6 показано, как поиск с возвратами решает задачу на рис. 10.4.

Каждая ветвь соответствует частичному присвоению (которое стано­вится полным, когда ветвь доходит до переменной 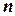) и уровень 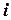дерева пред­ставляет выборы значений, сделанные для 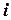-й переменной (согласно упорядоче­нию). Глубиной называется расстояние от корня дерева. Черные и белые вершины представляют соответственно успешные и неудачные присвоения в данной точке поиска. Вершины снабжены описанием значений доменов, при­писанных данной переменной в рассматриваемой точке поиска. Путь поиска показан пунктирной направленной линией.

Поиск с возвратами неэффективен в том смысле, что требует выполне­ния большего числа операций, чем это нужно для нахождения решения.

Для усовершенствования поиска с возвратами используются множества неперспективных наборов значений (МННЗ). В контексте задач выполнимости МННЗ соответствует клаузе (дизъюнкту), причем ис­пользование обучения и использования большого числа клауз во время по­иска оказалось весьма эффективным для решения задач выполнимости.