Индуцированный граф и индуцированная ширина задачи УО

Введем понятия индуцированного графа и индуцированной ширины (induced width) задачи УО, важные для применения структурных методов ре­шения задач УО. Индуцированная ширина определяется в терминах графа ограничений задачи УО.

Используем понятие упорядочения графа или задачи УО.

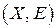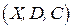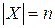Определение 10.4. Рассмотрим граф или задачу УО , где . Упорядочением для графа или задачи УО называется биекция .

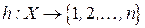Упорядочение 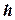соответствует вершинам или переменным, просматри­ваемым в порядке 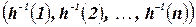. Если две переменные соединены в графе ребром, иногда полезно представить первую переменную, которая стоит раньше в упорядочении, в виде «родителя», а вторую ‑ как «сына» пер­вой вершины.

Перед определением индуцированной ширины введем более простое понятие ширины графа.

Определение 10.5. Пусть 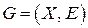‑ граф, а ‑ некоторое упорядочение вершин этого графа. Шириной вершины 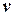для этого упорядочения 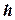называется число вер­шин, соединенных с 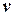и предшествующих ей в этом упорядочении (т.е. число родителей 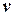). Шириной графа для упорядочения 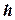называется максимальная ширина всех вершин для этого упорядочения. И наконец, шириной графа на­зывается минимальная ширина для всех упорядочений. Например, дерево имеет ширину 1, а полный граф с 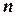вершинами имеет ширину 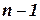. Введем далее следующие определения:

Определение 10.6. Шириной задачи УО для данного упорядочения называ­ется ширина его графа ограничений для этого упорядочения, а ширина ЗУО определяется как ширина ее графа ограничений.

Введем понятие индуцированного графа по отношению к данному упо­рядочению.

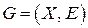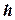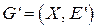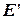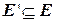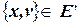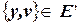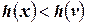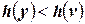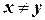Определение 10.7. Для данного графа и упорядочения , индуци­рованный граф определяется как граф с минимальным множеством ребер , таких что , и если , , , , и , то .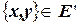

Индуцированный граф может быть построен за один проход, обрабаты­вая вершины исходного графа в обратном порядке; то есть вначале соединяем родителей последней вершины, затем родителей предпоследней вершины и т.д.

Определение 10.8. Индуцированная ширин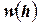а графа 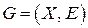по отно­шению к упорядочению 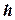‑ это ширина индуцированного графа 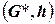по отношению к этому упорядочению.

Индуцированная ширина 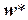графа ‑ это его минимальная индуцирован­ная ширина по всем упорядочениям.

Индуцированная ширина задачи УО по отношению к упорядочению 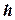‑ это индуцированная ширина ее графа ограничений по отношению к этому упорядочению, а индуцированная ширина задачи УО ‑ это индуцированная ширина ее графа ограничений. Синоним индуцированной ширины ‑ древо­видная ширина (см. раздел 8.5.3).

Известно, что данная задача УО при заданном упорядочении может быть решена за время, экспоненциальное от индуцированной ширины по от­ношению к этому упорядочению.

Хордальные графы

Граф называется хордальным, если каждый цикл длины 4 имеет хорду.

Многие трудные графовые задачи легко решаются на хордальных гра­фах. Вычисление индуцированной ширины достаточно несложно для хор­дальных графов. Например, нахождение всех максимальных клик в графе, что является NP-полной задачей на графах общего вида, легко произвести для хордальных графов. Эта задача (поиск максимальных клик в хордальных графах) облегча­ется за счет использования процедуры упорядочения max-cardinality.

Упорядочение max-cardinality[7] графа упорядочивает вершины, начиная от первой, согласно следующему правилу: первая вершина выбирается произвольно. После этого, следующей выбирается вершина, соединенная с максимальным числом уже упорядочен­ных вершин и т.д. Можно показать, что упорядочение max-cardinality может быть исполь­зовано для распознавания хордальных графов. Именно, граф ‑ хордальный, тогда и только тогда, когда при упорядочении max-cardinality каждая вершина вместе с ее предками образует клику. Можно таким образом перечислить все максимальные клики, соответ­ствующие каждой вершине (записывая множества, состоящие из каждой вершины и ее родителей, и определяя затем максимальный размер клики). Заметим, что в хордальном графе имеется не более 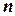клик, состоящих из вер­шин и их предков.

Кроме того, при использовании упорядочения max-cardinality хордаль­ного графа, упорядоченный граф идентичен его индуцированному графу и, значит, его ширина равна его индуцированной ширине. Справедливо

Предложение. Если 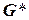‑ индуцированный граф графа 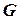для некото­рого упорядочения, тогда граф 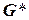‑ хордальный.