Уравнения равновесия жидкости
Выделим в покоящейся жидкости вокруг точки А элементарный объем в виде параллелепипеда (рис. 2.4) и составим условия его равновесия.
На этот параллелепипед выделенной жидкости действуют поверхностные силы (силы гидростатического давления) и объемные силы.
Примем, что давление в центре параллелепипеда (в точке А) равно pА. Тогда давление в центре левой грани p1 будет
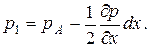
Сила давления на всю левую грань
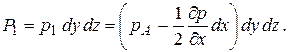
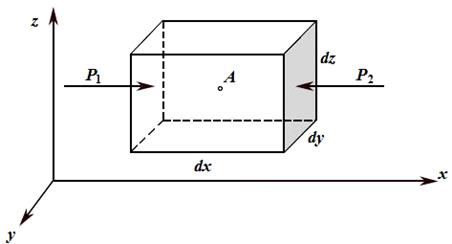
Рис. 2.4
Аналогично, сила давления на правую грань
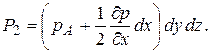
Здесь 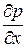 – изменение гидростатического давления по оси x на единицу длины. Знак этой величины определяется направлением перемещения от точки А к соответствующим граням: если перемещение противоположно направлению оси x – знак «минус», если совпадает с направлением оси x – знак «плюс».
– изменение гидростатического давления по оси x на единицу длины. Знак этой величины определяется направлением перемещения от точки А к соответствующим граням: если перемещение противоположно направлению оси x – знак «минус», если совпадает с направлением оси x – знак «плюс».
Проекция объемных сил на ось x будет равна 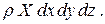
Тогда уравнение равновесия (покоя) выделенного объема жидкости можно записать в виде
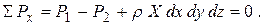
Подставляя значения P1 и P2 и приводя подобные члены, имеем
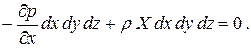
Сокращая на объем параллелепипеда 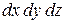 , получим уравнение для единицы объема жидкости
, получим уравнение для единицы объема жидкости
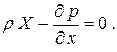
Уравнения для других осей запишем по аналогии:
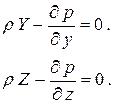
Эти уравнения называются уравнениями Эйлера. В них заключаются необходимые и достаточные условия равновесия жидкости, так как если эти условия выполняются в любой точке жидкости, то каждая частица жидкости находится в равновесии.
Обычно систему дифференциальных уравнений равновесия (уравнения Эйлера) записывают в следующем виде:
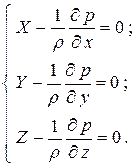
| (2.1) |
Уравнения Эйлера показывают, что в состоянии покоя массовые силы, действующие на каждую частичку жидкости, уравновешиваются поверхностными силами (градиентом давления).
Для вывода основного уравнения гидростатики необходимо проинтегрировать полученные дифференциальные уравнения равновесия (2.1).
Умножим каждый член первого из уравнений Эйлера на dx, второго и третьего – на dy и dz соответственно и сложим почленно. В результате получим
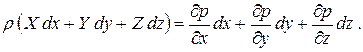
| (2.2) |
Очевидно, что правая часть уравнения (2.2) представляет собой полный дифференциал давления dp, поскольку давление является функцией координат 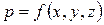 . Но если правая часть уравнения есть полный дифференциал, то, для того чтобы уравнение оставалось справедливым, и левая его часть должна быть полным дифференциалом какой-то функции. Тогда в случае однородной несжимаемой жидкости, то есть, когда ρ = const, существует некая функция координат U = f (x, y, z) которая обладает следующим свойством:
. Но если правая часть уравнения есть полный дифференциал, то, для того чтобы уравнение оставалось справедливым, и левая его часть должна быть полным дифференциалом какой-то функции. Тогда в случае однородной несжимаемой жидкости, то есть, когда ρ = const, существует некая функция координат U = f (x, y, z) которая обладает следующим свойством:
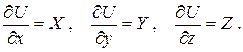
Силы, для которых такая функция существует, называются силами, имеющими потенциал. Функция U называется силовой потенциальной функцией.
Тогда уравнение равновесия (2.2) можно записать в виде
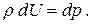
| (2.3) |
Из этого можно сделать вывод, что несжимаемая жидкость может находиться в равновесии только под действием объемных сил, имеющих потенциал.
Как известно, к таким силам относится, например, сила тяжести. Если на жидкость действует только одна объемная сила – сила тяжести, то можем записать
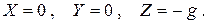
Уравнение равновесия тогда примет вид:
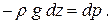
Считая ρ = const, интегрируем и получаем
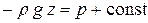 или или 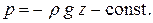
|
Отсюда видно, что в покоящейся жидкости, на которую действуют только силы тяжести, давление есть функция только одной вертикальной координаты – z. Это уравнение, записанное в виде
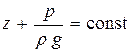 , ,
| (2.4) |
называют основным уравнением гидростатики.
Константу в уравнении (2.4) определим из граничного условия.
Расположим начало координат на поверхности жидкости, где p = p0, при z = 0. Тогда имеем: const = – p0.
Используем новую переменную – глубину погружения от поверхности жидкости h = – z. Тогда окончательно получим уравнение для гидростатического давления:
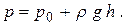
| (2.5) |
Таким образом, давление в любой точке жидкости, находящейся под действием силы тяжести, складывается из давления на поверхности и произведения объемного веса жидкости на глубину погружения этой точки. Из уравнения видно, что давление изменяется линейно с глубиной погружения.
Дата добавления: 2017-04-05; просмотров: 7950;











