Гидростатическое давление и его свойства

Напомним, что в разделе гидростатики исследуется жидкость, находящаяся в состоянии равновесия (или относительного покоя), скорости движения и угловые скорости сдвига равны нулю. В этом случае сопротивляемость жидкости сдвигающим и растягивающим усилиям отсутствует.

Введем понятие гидростатического давления.

Рассмотрим произвольный объем жидкости, находящийся в равновесии (рис. 2.1). Мысленно рассечем его плоскостью BC на две части I и II. Части I и II взаимодействуют по плоскости раздела. Отбросим мысленно первую часть рассматриваемого объема. При этом для сохранения равновесия второй части суммарное воздействие на нее отсеченной части заменим силой P. Сила воздействия, приходящаяся на площадку раздела, называется силой гидростатического давления.

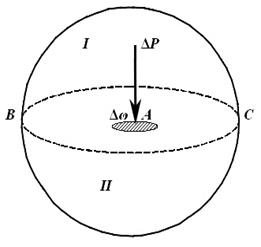
Рис. 2.1

Пусть площадь всей плоскости раздела равна ω. Отношение силы давления P к площади ω – это среднее гидростатическое давление на площади BC

.

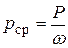Для того чтобы определить давление в некоторой точке A, выделим вокруг нее малую площадку Δω, сила, приходящаяся на эту площадку – ΔP.

Гидростатическим давлением в точке A называется предел

.

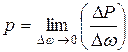Из определения текучести среды следует, что в состоянии покоя в жидкости касательные напряжения равны нулю, и в каждой точке произвольно ориентированной в пространстве площадки действуют только нормальные напряжения. Отсюда вытекает первое свойство гидростатического давления: гидростатическое давление всегда совпадает с направлением внутренней нормали к рассматриваемой площадке.

Предположим обратное – что сила гидростатического давления направлена не по нормали к поверхности выделенного объема. Тогда ее можно разложить на нормальную и касательную составляющие. Но касательная составляющая вызвала бы скольжение жидкости вдоль поверхности. А мы рассматриваем случай покоящейся жидкости, то есть неподвижной и находящейся в равновесии. Значит, на поверхности существуют только нормальные составляющие давления. Более того, они направлены внутрь рассматриваемого объема (иначе на поверхности возникли бы растягивающие напряжения, а их жидкости не воспринимают), следовательно, являются сжимающими.

Второе свойство гидростатического давления состоит в следующем: величина гидростатического давления в данной точке не зависит от направления той площадки, на которую оно действует.

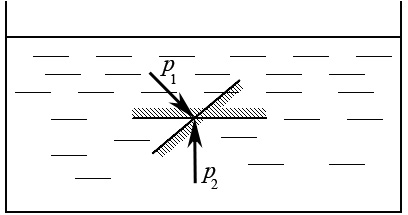
Рис. 2.2

Направление площадки будем характеризовать направлением нормали к ней. Второе свойство давления означает, что если через одну точку внутри жидкости провести две по-разному ориентированные площадки (рис. 2.2), то гидростатические давления p₁и p₂, действующие на этих площадках, по величине будут одинаковы, то есть .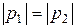

Для доказательства второго свойства давления выделим в неподвижной жидкой среде элементарный объем в форме тетраэдра (рис. 2.3) с ребрами, параллельными координатным осям и соответственно равными dx, dy, dz.

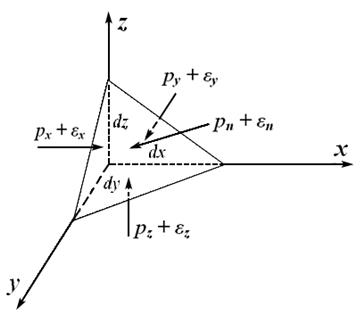
Рис. 2.3

Рассмотрим условия равновесия этого объема жидкости, мысленно отбросив окружающую его часть жидкости. В общем случае на тетраэдр действуют следующие силы:

· объемные силы, проекции на оси которых, приходящиеся на единицу массы, будут X, Y, Z;

· поверхностные силы со стороны отброшенной части жидкости.

Составим уравнение равновесия в проекции, например, на ось x.

Проекция на ось x объемных сил, действующих на тетраэдр, будет:

.

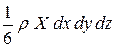Обозначим давление в центре координат – p, проекции его – p_x, p_y, p_z.

Тогда давление в центре тяжести грани dydz можем записать как (p_x + ε_x), где ε_x – малая величина. Аналогично, давление в центре тяжести грани dxdy будет (p_z + ε_z), в центре тяжести грани dxdz – (p_y + ε_y), в центре тяжести скошенной грани – (p_n + ε_n). Поверхностные силы, действующие на грани, получаем, умножая эти давления на площади соответствующих граней.

Поскольку давления на грани dxdy и dxdz перпендикулярны оси x, их проекции на эту ось будут нулевыми и уравнение равновесия в проекции на ось x будет:

.

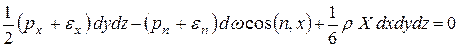Здесь dω – площадь скошенной грани тетраэдра, (n,x) – угол между осью x и нормалью к скошенной грани n.

Последним членом уравнения, как бесконечно малой величиной высшего порядка по отношению к другим членам уравнения, можно пренебречь.

Произведение dω cos (n,x) – это проекция скошенной грани на плоскость yz. Тогда

.

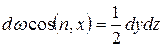С учетом этого из уравнения получаем

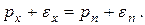
Так как размеры тетраэдра выбраны произвольно, то, уменьшая их (стягивая тетраэдр в точку), будем иметь: 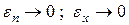. Из этого следует, что 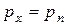. Рассуждая аналогично для проекций уравнения равновесия на другие оси, в результате получим:

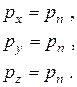
Следовательно,

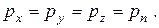
Направление n также выбрано произвольно, следовательно, гидростатическое давление не зависит от наклона площадки, на которую оно действует. При этом давление не будет одинаковым в разных точках пространства, занятого жидкостью, гидростатическое давление в точке зависит от ее координат в пространстве:

p = f (x, y, z).

Законы распределения давления в покоящейся жидкости и рассматриваются в гидростатике.

Заметим, что касательные напряжения в покоящейся жидкости равны нулю независимо от вязкости жидкости, а не только в идеальной жидкости.

Для сохранения сплошности жидкости давление в ней не должно быть меньше некоторого минимума, равного давлению насыщенных паров при данной температуре, то есть

p > p_min = p_н.п.

Если это условие не соблюдается, то при понижении давления ниже минимального происходит разрыв сплошности жидкости. Жидкость закипает – при понижении давления в ней начинается образование пузырьков пара. Это явление называется кавитацией.