Абсолютное и избыточное давление

Давление, отсчитываемое от абсолютного нуля, называется абсолютным давлением и обозначается p_абс. Абсолютный нуль давления означает полное отсутствие сжимающих напряжений.

В открытых сосудах или водоемах давление на поверхности равно атмосферному p_атм. Разность между абсолютным давлением p_абс и атмосферным p_атм называется избыточным давлением

p_изб = p_абс – p_атм.

Когда давление в какой-либо точке, расположенной в объеме жидкости, больше атмосферного, то есть 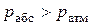, то избыточное давление положительно и его называют манометрическим.

Если давление в какой-либо точке оказывается ниже атмосферного, то есть 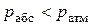, то избыточное давление отрицательно. В этом случае его называют разрежениемили вакуумметрическим давлением. За величину разрежения или вакуума принимается недостаток до атмосферного давления:

p_вак = p_атм – p_абс;

p_изб = – p_вак.

Максимальный вакуум возможен, если абсолютное давление станет равным давлению насыщенного пара, то есть p_абс = p_н.п. Тогда

p_{вак max} = p_атм – p_н.п.

В случае если давлением насыщенного пара можно пренебречь, имеем

p_{вак max} = p_атм.

Единицей измерения давления в СИ является паскаль (1 Па = 1 Н/м²), в технической системе – техническая атмосфера (1 ат = 1 кГ/см² = 98,1 кПа). При решении технических задач атмосферное давление принимается равным 1 ат = 98,1 кПа.

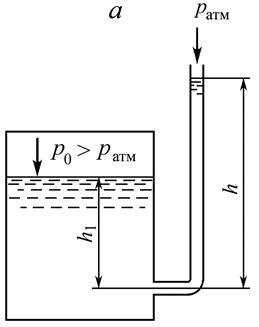
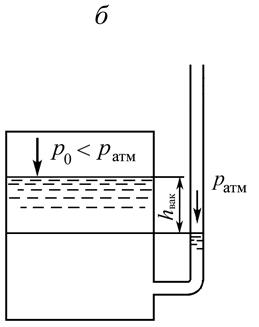
Манометрическое (избыточное) и вакуумметрическое (разрежение) давление часто измеряются с помощью стеклянных, открытых сверху трубок – пьезометров, присоединяемых к месту измерения давления (рис. 2.5).

Рис. 2.5

Пьезометры измеряют давление в единицах высоты подъема жидкости в трубке. Пусть трубка пьезометра присоединена к резервуару на глубине h₁ от поверхности жидкости в нем. Высота подъема жидкости в трубке пьезометра определяется давлением жидкости в точке присоединения. Давление в резервуаре на глубине h₁ определится из основного закона гидростатики в форме (2.5)

,

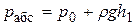где 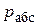– абсолютное давление в точке присоединения пьезометра;

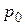– абсолютное давление на свободной поверхности жидкости.

Давление в трубке пьезометра (открытой сверху) на глубине h равно

.

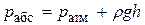Из условия равенства давлений в точке присоединения со стороны резервуара и в пьезометрической трубке получаем

.

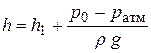(2.6)

Если абсолютное давление на свободной поверхности жидкости больше атмосферного (p₀ > p_атм) (рис. 2.5.а), то избыточное давление будет манометрическим, и высота подъема жидкости в трубке пьезометра h > h₁. В этом случае высоту подъема жидкости в трубке пьезометра называют манометрической или пьезометрической высотой.

Манометрическое давление в этом случае определится как

.

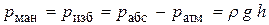Если абсолютное давление на свободной поверхности в резервуаре будет меньше атмосферного (рис. 2.5.б), то в соответствии с формулой (2.6) высота подъема жидкости в трубке пьезометра h будет меньше глубины h₁. Величину, на которую опустится уровень жидкости в пьезометре относительно свободной поверхности жидкости в резервуаре, называют вакуумметрической высотой h_вак (рис. 2.5.б).

Рассмотрим еще один интересный опыт. К жидкости, находящейся в закрытом резервуаре, на одинаковой глубине присоединены две вертикальные стеклянные трубки: открытая сверху (пьезометр) и запаянная сверху (рис. 2.6).

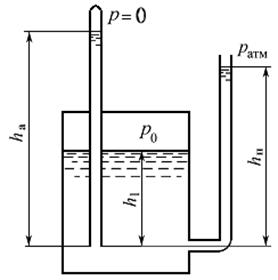
Рис. 2.6

Будем считать, что в запаянной трубке создано полное разряжение, то есть давление на поверхности жидкости в запаянной трубке равно нулю. (Строго говоря, давление над свободной поверхностью жидкости в запаянной трубке равно давлению насыщенных паров, но ввиду его малости при обычных температурах, этим давлением можно пренебречь).

В соответствии с формулой (2.6) жидкость в запаянной трубке поднимется на высоту, соответствующую абсолютному давлению на глубине h ₁:

.

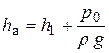А жидкость в пьезометре, как показано ранее, поднимется на высоту, соответствующую избыточному давлению на глубине h ₁.

Вернемся к основному уравнению гидростатики (2.4). Величина H, равная

,

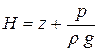(2.7)

где z – расстояние по вертикали от рассматриваемой точки до некоторой плоскости сравнения, называется гидростатическим напором в некоторой точке объема жидкости относительно плоскости сравнения.

Если в выражении (2.7) давление равно избыточному (p = p_изб), то величина

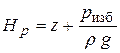
(2.8)

называется пьезометрическим напором.

Как следует из формул (2.7), (2.8), напор измеряется в метрах.

Согласно основному уравнению гидростатики (2.4) как гидростатический, так и пьезометрический напоры в покоящейся жидкости относительно произвольно выбранной плоскости сравнения являются постоянными величинами. Для всех точек объема покоящейся жидкости гидростатический напор одинаков. То же самое можно сказать и про пьезометрический напор.

Это значит, что если к резервуару с покоящейся жидкостью подключить на разной высоте пьезометры, то уровни жидкости во всех пьезометрах установятся на одинаковой высоте в одной горизонтальной плоскости, называемой пьезометрической.

Поверхности уровня

Во многих практических задачах бывает важно определить вид и уравнение поверхности уровня.

Поверхностью уровня или поверхностью равного давления называется такая поверхность в жидкости, давление во всех точках которой одно и то же, то есть на такой поверхности dp = 0.

Так как давление является некоторой функцией координат p = f(x,y,z), то уравнение поверхности равного давления будет:

Придавая константе C разные значения, будем получать различные поверхности уровня. Уравнение (2.9) есть уравнение семейства поверхностей уровня.

Свободная поверхность – это поверхность раздела капельной жидкости с газом, в частности, с воздухом. Обычно про свободную поверхность говорят только для несжимаемых (капельных) жидкостей. Понятно, что свободная поверхность является и поверхностью равного давления, величина которого равна давлению в газе (на поверхности раздела).

По аналогии с поверхностью уровня вводят понятие поверхности равного потенциала илиэквипотенциальной поверхности – это поверхность, во всех точках которой силовая функция имеет одно и то же значение. То есть на такой поверхности

U = const

или

.

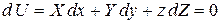Тогда уравнение семейства эквипотенциальных поверхностей будет иметь вид

U(x,y,z) = C,

где постоянная C принимает различные значения для разных поверхностей.

Из интегральной формы уравнений Эйлера (2.3) следует, что

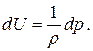
Из этого соотношения можно сделать вывод, что поверхности равного давления и поверхности равного потенциала совпадают, потому что при dp = 0и dU = 0.

Важнейшее свойство поверхностей равного давления и равного потенциала состоит в следующем: объемная сила, действующая на частицу жидкости, находящуюся в любой точке, направлена по нормали к поверхности уровня, проходящей через эту точку.

Докажем это свойство.

Пусть частица жидкости из точки с координатами 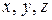переместилась по эквипотенциальной поверхности в точку с координатами 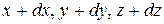. Работа объемных сил на этом перемещении будет равна

.

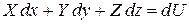Но, поскольку частица жидкости перемещалась по эквипотенциаль-ной поверхности, dU = 0. Значит работа объемных сил, действующих на частицу, равна нулю. Силы не равны нулю, перемещение не равно нулю, тогда работа может быть равна нулю только при условии, что силы перпендикулярны перемещению. То есть объемные силы нормальны к поверхности уровня.

Обратим внимание на то, что в основном уравнении гидростатики, записанном для случая, когда на жидкость действует только один вид объемных сил – силы тяжести (см. уравнение (2.5))

,

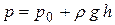величина p₀ – не обязательно давление на поверхности жидкости. Это может быть давление в любой точке, в которой оно нам известно. Тогда h – это разность глубин (по направлению вертикально вниз) между точкой, в которой давление известно, и точкой, в которой мы хотим его определить. Таким образом, с помощью этого уравнения можно определить значение давления p в любой точке через известное давление в известной точке – p₀.

Заметим, что величина не зависит от p₀. Тогда из уравнения (2.5) следует вывод: насколько изменится давление p₀, настолько же изменится и давление в любой точке объема жидкости p. Поскольку точки, в которых фиксируем p и p₀, выбраны произвольно, это означает, что давление, создаваемое в любой точке покоящейся жидкости, передается ко всем точкам занимаемого объема жидкости без изменения величины.

Как известно, в этом и состоит закон Паскаля.

По уравнению (2.5) можно определить форму поверхностей уровня покоящейся жидкости. Для этого надо положить p = const. Из уравнения следует, что это выполнимо лишь при h = const. Значит, что при действии на жидкость из объемных сил только сил тяжести, поверхности уровня представляют собой горизонтальные плоскости. Такой же горизонтальной плоскостью будет и свободная поверхность покоящейся жидкости.

Учитывая вышесказанное, можно сформулировать еще одно свойство гидростатического давления:

Гидростатическое давление в любой точке жидкости на одной высоте по всем направлениям одинаково.

Из этого свойства вытекает и закон сообщающихся сосудов с жидкостью.

Сообщающимися сосудами называются сосуды, соединенные друг с другом таким образом, чтобы жидкость свободно перетекала из одного сосуда в другой.

Закон сообщающихся сосудов гласит: в открытых сообщающихся сосудах при равновесии жидкости давление на любом горизонтальной уровне одинаково.

Если в открытые сообщающиеся сосуды налита одинаковая жидкость, то независимо от формы сосудов жидкость в этих сосудах будет находиться на одном уровне (рис. 2.7.а).

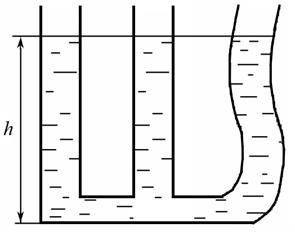
Если заполнить открытые сообщающиеся сосуды двумя несмешивающимися жидкостями, имеющими плотности ρ₁ и ρ₂, например, ртутью и водой (рис. 2.7.б), то жидкость в сосудах распределится таким образом, чтобы давление на любом горизонтальной уровне в обоих сосудах было одинаково. Выберем горизонтальный уровень жидкости AB, ниже которого жидкость однородна (рис. 2.7.б).

а	б

Рис. 2.7

Тогда p₁ = p₂.

В соответствии с формулой (2.5) для гидростатического давления в разных сосудах будем иметь

;

.

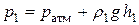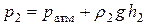Откуда следует, что

.

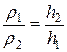(2.10)

Уравнение (2.10) представляет собой условие равновесия жидкостей в сообщающихся сосудах. Как частный случай из него следует, что если в сообщающиеся сосуды налита одна жидкость (то есть ρ₁ = ρ₂), то уровень жидкости в сосудах будет одинаковым: h₁ = h₂.