Силы, действующие в покоящейся жидкости

Раздел гидравлики, изучающий законы равновесия жидкости и нахождения ее в покое, называется гидростатикой. Исходя из гипотезы сплошности, будем считать, что жидкость сплошным образом занимает пространство, и все искомые характеристики жидкости будут непрерывными функциями координат.

На жидкость и при равновесии, и при движении действуют силы внешние и внутренние.

Внутренние силы – это силы взаимодействия между частицами жидкости. Согласно третьему закону Ньютона, они взаимно уравновешиваются, и не влияют на равновесие или процесс движения рассматриваемых объемов жидкости. Поэтому, при изучении процессов гидравлики, они, как правило, не принимаются во внимание.

Внешние силы – это силы взаимодействия рассматриваемого объема жидкости с окружающей средой. В гидравлике такие силы разделяют на объемные (массовые) и поверхностные.

Объемные силы действуют на каждую частицу жидкости в рассматриваемом объеме. В соответствии со вторым законом Ньютона, эти силы пропорциональны массе жидкости или (для однородной жидкости) ее объему. Коэффициент пропорциональности – ускорение частицы

,

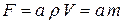где a – ускорение движущейся частицы жидкости;

ρ – плотность жидкости;

V и m – соответственно объем и масса частицы жидкости.

Примеры объемных сил – силы тяжести, силы инерции, электромагнитные силы (если жидкость несет электрический заряд).

Далее мы часто будем использовать понятие единичной массовой силы, то есть массовой силы, приходящейся на единицу массы жидкости – 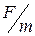. Проекции единичной массовой силы на оси декартовых координат будем обозначать через X, Y, Z. Эти величины имеют размерность ускорения. Например, если на жидкость действует сила тяжести, то проекции X, Y равны нулю, а проекция Z = – g (сила действует в отрицательном направлении оси z).

Поверхностные силы возникают в местах контакта рассматриваемого объема жидкости с соседними: со стенками сосуда или трубы, с поверхностью раздела с газообразной средой, с соседними объемами жидкости.

Поверхностные силы непрерывно распределены по поверхности жидкой частицы и зависят от площади этой поверхности, но не зависят от объема (массы) частицы. Такие силы обусловлены воздействием на рассматриваемый объем жидкости соседних объемов или соприкасающихся с ним тел (твердых или газообразных). В общем случае поверхностная сила, действующая на некоторую площадку поверхности, направлена под некоторым углом к ней. Значит, ее можно разложить на нормальную и касательную составляющие. Нормальная составляющая – это сила давления, касательная составляющая – сила трения. Приходящаяся на единицу площади поверхностная сила называется напряжением.

Нормальное напряжение – это гидромеханическое (в частном случае покоя – гидростатическое) давлениеp, касательное напряжение – это напряжение трения τ.

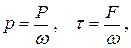
где P – нормальная к площадке поверхностная сила,

F – касательная к площадке поверхностная сила,

ω – площадь, на которую действуют поверхностные силы.

Эти формулы справедливы, если поверхностные силы равномерно распределены по поверхности площадки ω. В общем случае неравномерного распределения сил напряжение в конкретной точке поверхности находим, устремляя к нулю рассматриваемую элементарную площадку, то есть, стягивая ее в точку:

.

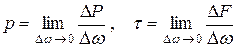Смысл разделения поверхностного напряжения на нормальное и касательное заключается, прежде всего, в том, что различна их роль в практических задачах. Например, при движении жидкости в трубах нормальное напряжение (давление) определяет прочность стенок, а касательное – сопротивление движению. При обтекании тел касательные напряжения действуют только в узком пограничном слое и быстро уменьшаются с удалением от стенки, в то время как нормальные напряжения (давление) по толщине пограничного слоя практически не меняются. Если выделить какой-то объем за пределами пограничного слоя, то на его поверхности действуют только силы давления. То же самое происходит и в случаях равновесия жидкости – касательные напряжения отсутствуют.