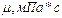АНАЛИЗ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ УСТАНОВИВШИХСЯ И НЕУСТАНОВИВШИХСЯ ПРИТОКОВ ЖИДКОСТИ К ГОРИЗОНТАЛЬНОЙ СКВАЖИНЕ И ВЕРТИКАЛЬНОЙ ТРЕЩИНЕ
Разработанные алгоритмы использованы для исследования установившегося и неустановившегося притока к горизонтальным скважинам.
При установившемся притоке рассмотрена задача для расчета протяженности горизонтального ствола к горизонтальным газовым скважинам. Исходные данные для расчета имеют следующие значения: постоянный расход газа, закачиваемого в хранилище – 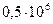
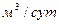 , радиус скважины -
, радиус скважины - 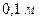 , толщина пласта –
, толщина пласта – 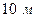 , коэффициент проницаемости –
, коэффициент проницаемости – 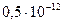 м2, вязкость газа –
м2, вязкость газа – 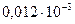
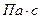 , относительная плотность газа –
, относительная плотность газа – 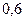 , глубина вертикального ствола –
, глубина вертикального ствола – 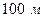 , средняя величина сверхсжимаемости газа –
, средняя величина сверхсжимаемости газа – 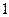 , коэффициент гидравлического сопротивления в вертикальных трубах -
, коэффициент гидравлического сопротивления в вертикальных трубах - 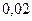 , стандартное давление-
, стандартное давление- 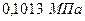 , плотность газа в стандартных условиях -
, плотность газа в стандартных условиях - 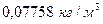 , коэффициент пористости -
, коэффициент пористости - 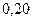 .
.
Для проведения системного анализа влияния дебита на длину горизонтального участка при разных условиях, получены зависимости влияния дебита на протяженность ствола скважины при меняющемся коэффициенте проницаемости.
|
| |
| |
| |
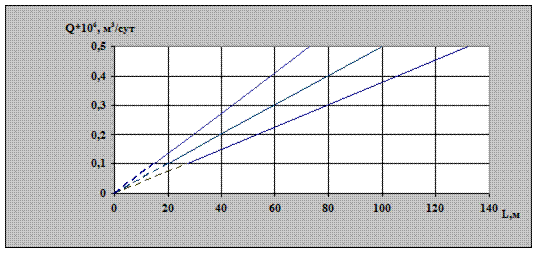
Рис. 2.1. Зависимость расхода газа от длины горизонтального
ствола и от коэффициента проницаемости (площадь
дренирования квадрат и учитывается кривизна)
На рис. 2.1 представлена зависимость дебита горизонтальной скважины от длины при разных коэффициентах проницаемости коллектора. Из рисунка видно, что при увеличении длины горизонтального ствола на 20 м дебит горизонтальной газовой скважины возрастает на 3,3%. Например, при увеличении коэффициента проницаемости на 45% при длине ствола 60м расход газа возрастает на 9%. Это позволяет сделать вывод о том, что чем больше длина горизонтального ствола, тем больше дебит газа. График имеет прямолинейный вид, так как мы рассматриваем установившийся приток. На рис. 2.2. представлена та же зависимость только в варианте 3D, где аналогично можно проследить рост дебита при увеличении длины и росте коэффициента проницаемости.
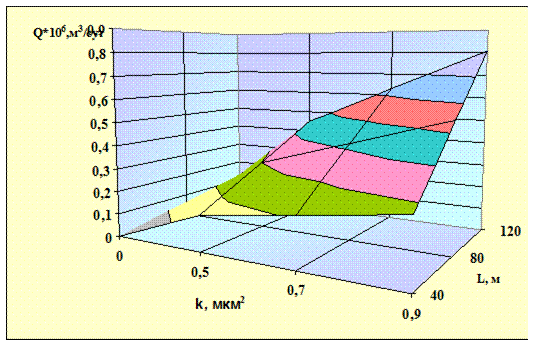
Рис. 2.2. Зависимость дебита от коэффициента проницаемости и длины горизонтального ствола
|
| |
| |
| |
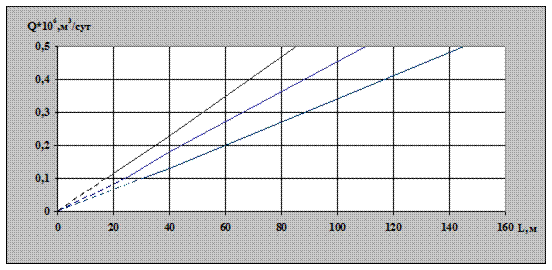
Рис. 2.3. Зависимость расхода газа от длины горизонтального
ствола и от коэффициента проницаемости (площадь
дренирования квадрат и не учитывается кривизна)
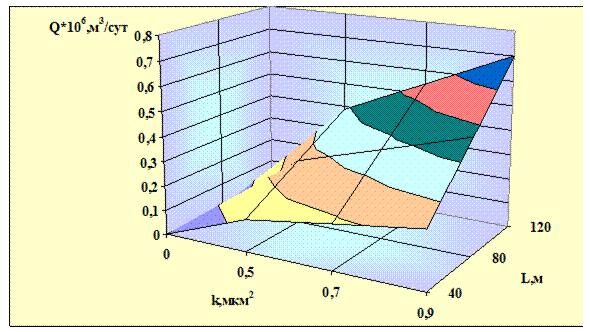
Рис. 2.4. Зависимость дебита от коэффициента проницаемости
и длины горизонтального ствола
На рис. 2.3, 2.4 представлены аналогичные зависимости расхода газа от длины горизонтального ствола в 2D и 3D варианте при увеличении коэффициента проницаемости от 0,5 до 0,9 мкм2, то есть на 45% без учета кривизны перехода от вертикального ствола в горизонтальный. При учете кривизны перехода и увеличении длины горизонтального участка на 20 м расход газа увеличивается на 3,3%, что на 0,9% больше, чем в случае без учета кривизны. При длине горизонтального ствола 60м расход газа, при прочих равных условиях, снизился на 7,2%.
|
| |
| |
| |
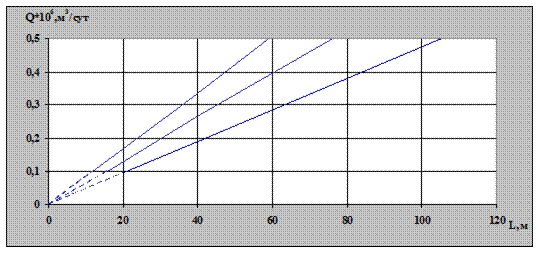
Рис. 2.5. Зависимость расхода газа от длины горизонтального
ствола и от коэффициента проницаемости (площадь
дренирования круг и учитывается кривизна)
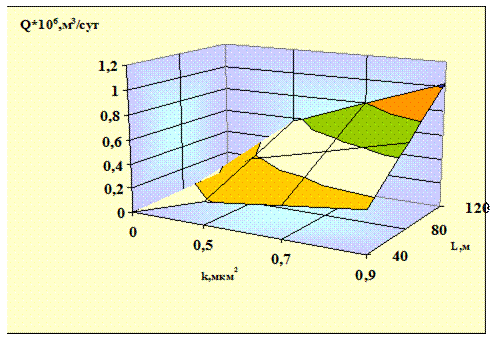
Рис. 2.6. Зависимость дебита от коэффициента проницаемости и длины горизонтального ствола
На рис. 2.5, 2.6 приведены зависимости расхода газа от длины горизонтального ствола в 2D и 3D варианте при изменении коэффициента проницаемости от 0,5 до 0,9 мкм2, когда площадь дренирования круг и учитывается кривизна перехода от вертикального ствола в горизонтальный.
В этом случае наглядно видно, что увеличении длины на 20м влечет за собой рост расхода газа на 5,3%, что на 2% больше чем когда площадь дренирования квадрат. А при изменении коэффициента проницаемости на 45% при длине горизонтального ствола 60м расход увеличивается на 14,2%.
|
| |
| |
| |
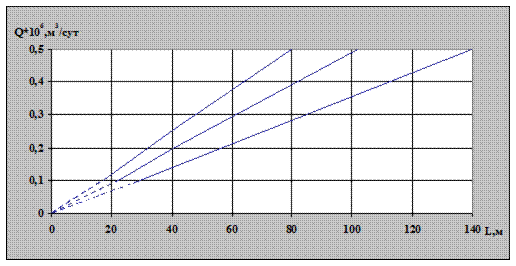
Рис. 2.7. Зависимость расхода газа от длины горизонтального
ствола и от коэффициента проницаемости (площадь
дренирования круг и не учитывается кривизна)
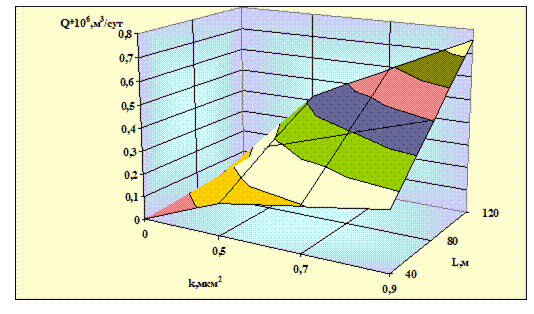
Рис. 2.8. Зависимость дебита от коэффициента проницаемости и длины горизонтального ствола
На рис. 2.7, 2.8 показаны зависимости расхода газа от длины горизонтального ствола в 2D и 3D варианте, а также при изменении коэффициента проницаемости от 0,5 до 0,9 мкм2, когда площадь дренирования круг и не учитывается кривизна перехода от вертикального ствола в горизонтальный.
Для этого случая при увеличении длины горизонтального участка на 20м расход газа снизился по сравнению с учетом кривизны на 2,4%. А при изменении коэффициента проницаемости с 0,5 по 0,9 мкм2 при длине горизонтального ствола 60м снизился на 6,5%.
|
| |
| |
| |
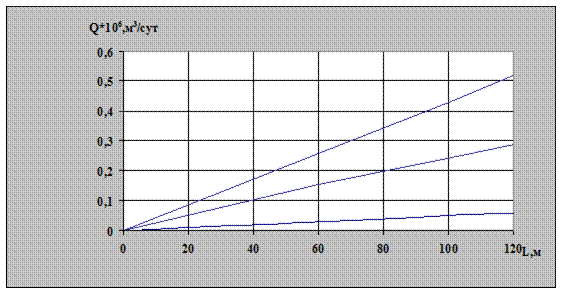
Рис. 2.9. Зависимость дебита газа от длины горизонтального ствола при различных параметрах анизотропии
|
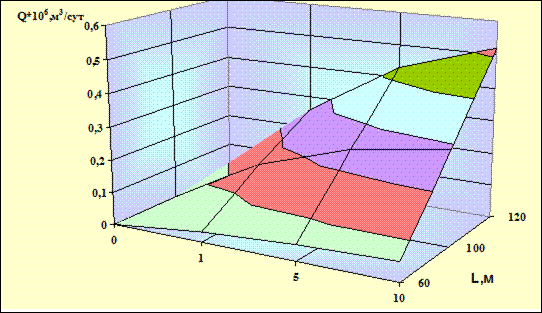
Рис. 2.10. Зависимость дебита от длины горизонтального ствола
и коэффициента анизотропии
На рис. 2.9, 2.10 показана зависимость дебита газа от длины горизонтального ствола при различных значениях анизотропии. Из рисунка видно, что зависимость длины ствола от дебита скважины имеет линейный характер. Влияние коэффициента анизотропии имеет обратную зависимость. Например, при χ=10 и χ=1 и длине горизонтального ствола 100 м дебит скважин равен 50000 и 430000  соответственно, то есть десятикратное увеличение анизотропии приводит к уменьшению дебита скважины в 8,6 раза.
соответственно, то есть десятикратное увеличение анизотропии приводит к уменьшению дебита скважины в 8,6 раза.
|
| |
| |
| |
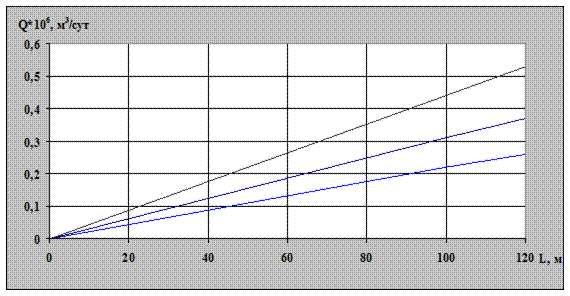
Рис. 2.11. Зависимость дебита газа от длины горизонтального ствола
при различных значениях толщины пласта
Зависимости расхода газа от длины ствола и толщины пласта приведены на рис. 2.11 и 2.12. Наглядно можно увидеть, что при увеличении длины ствола на 40 м дебит скважины увеличивается на 1,6%, а при увеличении толщины пласта с 5 до 15 м при длине горизонтального участка 100 м расход газа увеличивается на 9,2%.
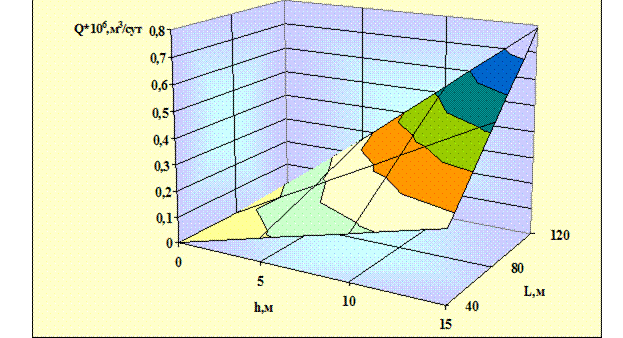
Рис. 2.12. Зависимость дебита от толщины пласта
и длины горизонтального ствола
При неустановившемся притоке была рассмотрена задача для расчета дебита вертикальной трещины. Исходные данные для расчета имеют следующие значения: радиус скважины – 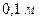 , коэффициент динамической вязкости жидкости –
, коэффициент динамической вязкости жидкости – 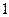
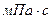 , коэффициент проницаемости пласта –
, коэффициент проницаемости пласта – 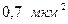 , длина пласта –
, длина пласта – 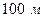 , толщина пласта –
, толщина пласта – 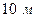 , давление на контуре –
, давление на контуре – 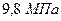 , давление в трещине –
, давление в трещине – 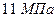 , коэффициент анизотропии –
, коэффициент анизотропии – 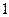 .
.
Для проведения системного анализа влияния толщины вскрытия на удельный расход трещины и на дебит при разных значениях анизотропии и вязкости были получены следующие зависимости.
На рис. 2.13, 2.14 представлены зависимости удельного расхода трещины от степени вскрытия пласта и величины. Из рисунков видно, что степень вскрытия пласта прямопропорциональна удельному расходу трещины. Но при учете анизотропии пласта наблюдается обратная зависимость. То есть расход трещины больше, чем меньше величина анизотропии. Например, при степени вскрытия и коэффициенте анизотропии равных 1, расход будет составлять 0,88 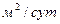 , что на 26,4% больше, чем при коэффициенте анизотропии χ =10.
, что на 26,4% больше, чем при коэффициенте анизотропии χ =10.
|
| |
| |
| |
|
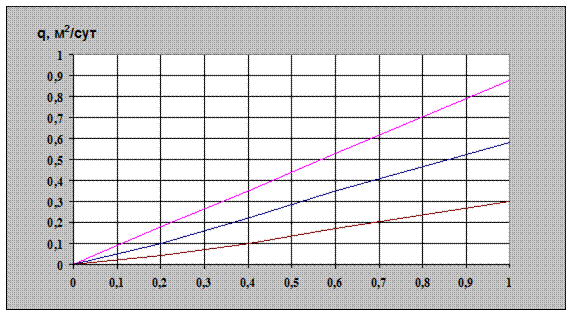
Рис. 2.13. Графическая зависимость удельного расхода трещины
от степени вскрытия пласта и анизотропии
|
|
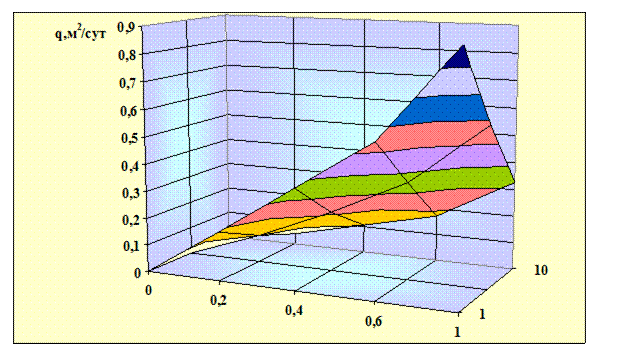
Рис. 2.14. Зависимость дебита от степени вскрытия
и анизотропии пласта
На рис. 2.15, 2.16 приведены зависимости дебита вертикальной трещины от вязкости жидкости при разных коэффициентах. Из рисунков можно заметить, что с увеличением вязкости жидкости дебит снижается. Зато изменение коэффициента проницаемости на 45% при вязкости жидкости, равной 1  , влечет за собой увеличение дебита на 40
, влечет за собой увеличение дебита на 40  .
.
|
| |
| |
| |
|
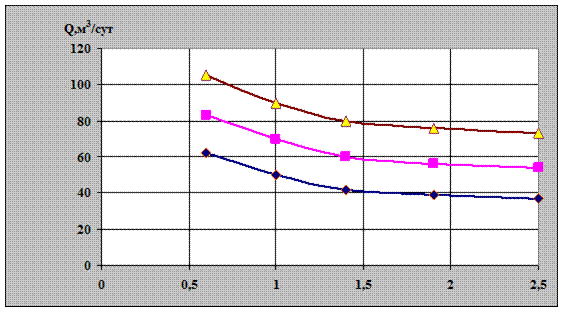
Рис. 2.15. Зависимость дебита вертикальной трещины
от вязкости жидкости
|
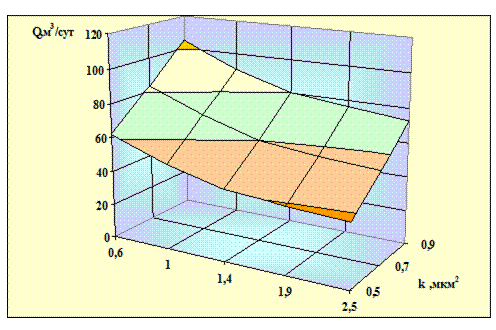
Рис. 2.16. Зависимость дебита от вязкости жидкости и коэффициента проницаемости
Зависимости дебита вертикальной трещины от степени вскрытия при изменении коэффициента вязкости жидкости приведены на рис. 2.17 и 2.18. Из рисунков видно, что с увеличением степени вскрытия пласта дебит увеличивается. Про вязкость можно сказать обратное, чем больше вязкость жидкости, тем меньше дебит трещины. Например, при степени вскрытия пласта 0,8 и вязкости жидкости, равной 1 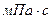 , дебит составил 80
, дебит составил 80 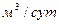 , что на 34
, что на 34 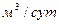 меньше, чем при вязкости, равной 3
меньше, чем при вязкости, равной 3 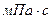 .
.
|
|
| |
| |
| |
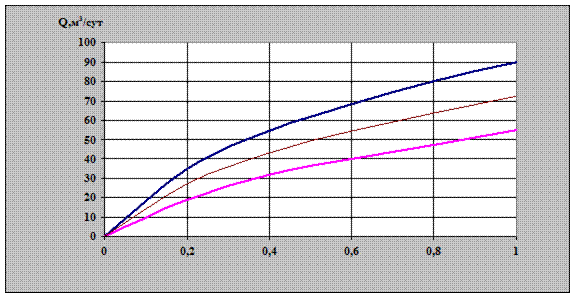
Рис. 2.17. Зависимость дебита вертикальной трещины
от степени вскрытия пласта
|
|
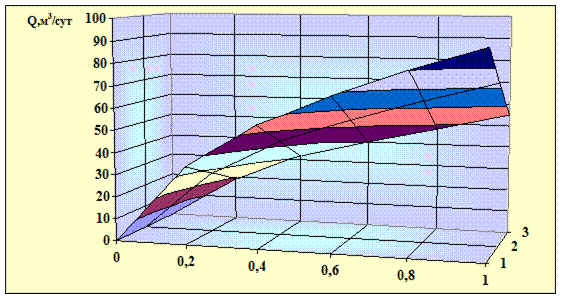
Рис. 2.18. Зависимость дебита от степени вскрытия пласта  и динамической вязкости жидкости
и динамической вязкости жидкости
Таким образом, проведенные исследования показали, что при установившемся притоке длина горизонтального ствола скважины зависит от расхода закачиваемого газа, величины объема дренирования и способа перехода от вертикального ствола в горизонтальный. Рассмотренные зависимости позволили сделать соответствующие выводы, что с ростом расхода газа увеличивается и длина. Кроме того, с увеличением коэффициента проницаемости наблюдаем возрастание дебита скважин. Влияние коэффициента анизотропии имеет обратную зависимость от дебита, чем меньше анизотропия, тем больше дебит газа.
При неустановившемся притоке удельный расход вертикальной трещины зависит от степени вскрытия пласта коэффициента анизотропии и динамической вязкости жидкости. Рассмотренные зависимости позволили сделать выводы, что чем меньше коэффициент анизотропии, тем больше удельный расход. Увеличение динамического коэффициента вязкости жидкости приводит к снижению дебита вертикальной трещины.
| |
Р А З Д Е Л V
Дата добавления: 2017-04-05; просмотров: 2531;

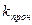 =0,5 мкм2
2 -
=0,5 мкм2
2 - 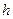 =5м
2 -
=5м
2 - 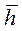
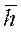
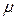
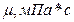
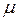 =1
=1 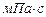 2 -
2 -