Поверхность жидкости во вращающемся сосуде

Определим, какую форму принимает поверхность жидкости в равномерно вращающемся сосуде. Свободная поверхность и здесь будет поверхностью уровня, только на этот раз это будет уже не горизонтальная плоскость, поскольку на жидкость из объемных сил действует не только сила тяжести.

При равномерном вращении сосуда с жидкостью поставленную задачу можно рассматривать как гидростатическую, жидкость будет находиться в покое относительно стенок сосуда, то есть здесь будет наблюдаться случай «относительного покоя». При этом жидкость будет находиться в равновесии под действием двух объемных сил: силы тяжести и силы инерции – центробежной силы. На каждую частицу жидкости во вращающемся сосуде действуют обе эти силы.

Центробежная сила, действующая на частицу жидкости, находящуюся в некоторой произвольной точке М (рис. 2.8), для кругового движения определится по формуле

.

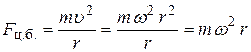Здесь r – радиус окружности (расстояние от точки до оси вращения), по которой вращается частица жидкости, находящаяся в точке М,

ω – угловая скорость вращения,

m – масса частицы жидкости.

Удельная центробежная сила, то есть сила, отнесенная к единице массы, будет равна

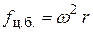
Проекции удельной центробежной силы на оси координат определятся как (рис. 2.8)

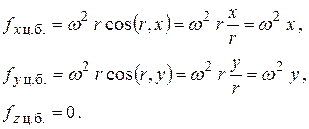
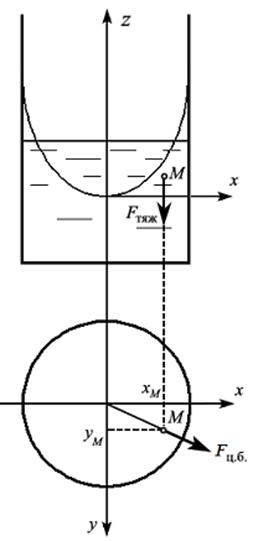
Рис. 2.8

Проекции удельной силы тяжести на оси

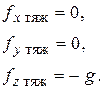
Суммарно для проекций удельных объемных сил, действующих на частицу жидкости, получаем

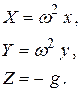
Вспомним дифференциальное уравнение равновесия жидкости:

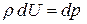
или

.

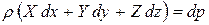Подставим в него значения проекций объемных сил:

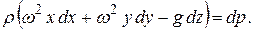
Проинтегрируем уравнение, считая ρ величиной постоянной. Имеем

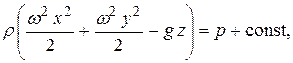
или

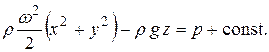
Заметим, что при вращении жидких частиц по круговым траекториям

.

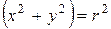Для определения константы интегрирования сформулируем граничные условия. Обратим внимание на то, что при вращении свободная поверхность жидкости примет симметричную вогнутую форму. Расположим начало координат в низшей точке свободной поверхности. На свободной поверхности жидкости давление равно атмосферному.

Тогда граничное условие формулируется так: при x = y = z = 0 давление p = p_атм.

Определяя из этого условия константу интегрирования, получим:

const = – p_атм.

Уравнение для определения давления примет вид:

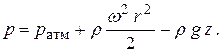
(2.11)

По этой формуле можно вычислить давление в любой точке внутри объема жидкости, находящейся в сосуде, вращающемся с постоянной угловой скоростью.

Как определить форму свободной поверхности жидкости? Свободная поверхность является поверхностью уровня, то есть поверхностью равного давления. Давление во всех ее точках равно атмосферному p = p_атм. Используя это условие, из уравнения (2.11) получаем

,

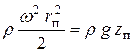где индекс «п» относится к координатам точек, находящихся на поверхности жидкости. Окончательно имеем

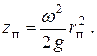
(2.12)

Уравнение (2.12) дает зависимость вертикальной координаты точек, расположенных на свободной поверхности жидкости, от расстояния до оси вращения: 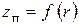. Это и есть уравнение свободной поверхности жидкости, находящейся в равномерно вращающемся сосуде. Видно, что форма свободной поверхности – параболоид вращения с вертикальной осью симметрии.