Виды выходных функций.
· Детерминированная функция (DT) – все дуги, выходящие из узла, выполняются, если узел активирован.
· Стохастическая функция (ST) – только одна дуга, выходящая из узла, выполняется с заданной вероятностью, если узел активирован.
Графическое изображение описанных узлов приведено на рисунке 5.22.

Рис. 5.22 Графическое изображение входных и
выходных узлов ГЕРТ-сети
Комбинация всех входных и выходных функций дает шесть различных типов узлов, показанных на рисунке 5.23.
Рис. 5.23 Возможные комбинации входных и выходных функций
5.4.2 Производящие функции ГЕРТ-сетей
Как отмечалось выше, каждая дуга 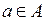 ГЕРТ-сети характеризуется вероятностью выполнения данной дуги
ГЕРТ-сети характеризуется вероятностью выполнения данной дуги 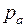 , а также распределением вероятностей значения параметра, передаваемого по сети. Пусть
, а также распределением вероятностей значения параметра, передаваемого по сети. Пусть 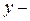 случайная величина, характеризующая процесс на дуге
случайная величина, характеризующая процесс на дуге 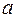 (например, время выполнения операции) с условной плотностью распределения
(например, время выполнения операции) с условной плотностью распределения 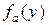 . Таким образом, полная характеристика дуги
. Таким образом, полная характеристика дуги 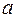 представляет собой вектор
представляет собой вектор 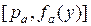 . Наряду с распределениями
. Наряду с распределениями 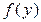 мы будем рассматривать порождаемые ими функции
мы будем рассматривать порождаемые ими функции 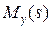 , которые носят название производящих функций и вычисляется следующим образом.
, которые носят название производящих функций и вычисляется следующим образом.
Для случайной величины с непрерывным распределением 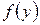
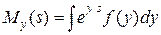 , (5.24)
, (5.24)
где 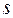 - вещественный параметр, а интеграл берется по всей области определения случайной величины
- вещественный параметр, а интеграл берется по всей области определения случайной величины 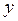 .
.
Для случайной величины с дискретным распределением
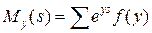 , (5.25)
, (5.25)
где суммирование производится по всем значениям 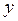 .
.
Предполагается, что интеграл в (5.24) и сумма в (5.25) конечны.
Использование производящих функций позволяет оценивать вероятностные характеристики сложных систем, описываемых ГЕРТ‑сетями, более просто, чем при работе непосредственно с распределениями случайных величин. При этом важным свойством производящей функции случайной величины является возможность вычислять начальные моменты распределения 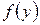 . Напомним, что k-м начальным моментом случайной величины
. Напомним, что k-м начальным моментом случайной величины 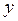 с непрерывной функцией плотности распределения
с непрерывной функцией плотности распределения 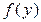 называется интеграл
называется интеграл
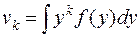 , k = 0, 1, … . (5.26)
, k = 0, 1, … . (5.26)
В частности, 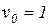 ,
, 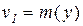 ‑ математическое ожидание случайной величины
‑ математическое ожидание случайной величины 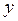 ; второй момент
; второй момент 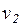 позволяет определить дисперсию случайной величины:
позволяет определить дисперсию случайной величины: 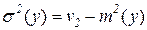 .
.
Справедливо утверждение [32]: начальные моменты 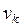 распределения случайной величины
распределения случайной величины 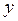 , заданного функцией
, заданного функцией 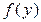 , равны значениям
, равны значениям 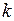 -й производной от функции
-й производной от функции 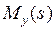 в точке
в точке 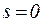 :
:
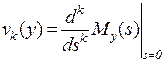 ,
, 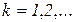 . (5.27)
. (5.27)
В частности, первый момент, т.е. математическое ожидание случайной величины определяется выражением
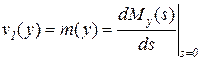 , (5.28)
, (5.28)
а второй момент
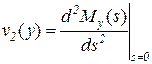 . (5.29)
. (5.29)
В таблице 5.3 приведены выражения для некоторых функций распределения, их производящих функций, и первых двух моментов
Использование производящих функций позволяет представить характеристику дуги  в виде вектора
в виде вектора 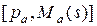 , а произведение этих компонентов
, а произведение этих компонентов
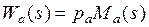 (5.30)
(5.30)
называется передаточной функцией дуги 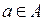 или ее W-функцией.
или ее W-функцией.
Смысл передаточной функции заключается в следующем. Если во входном узле ni некоторой дуги aij действует сигналy, то в выходной узел этой дуги nj поступит сигнал x=Wij(s)y.
Понятие передаточной функции используется во многих научных дисциплинах, связанных с изучением динамических процессов – в электротехнике, радиотехнике, теории управления и других. Особенность W‑функций, применяемых в ГЕРТ-сетях состоит в том, что W(s) - функция является вещественной функцией вещественного аргумента, в отличие от других определений передаточных функций, которые рассматриваются как комплексные функции комплексного аргумента. Кроме того, преобразование сигнала происходит не в узлах, а на дугах.
Таблица 5.3
Характеристики некоторых распределений
Тип распределения
| Производящая функция
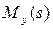
| Мат.
ожида-ние 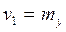
| Второй момент
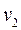
| Пара-метры распре-деления |
Дискретное 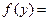
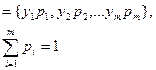
| 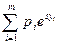
| 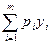
| 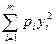
| 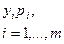
|
Биномиальное
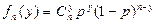
| 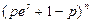
| 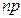
| 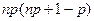
| 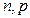
|
Экспоненциальное
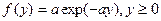
| 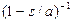
| 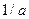
| 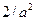
| 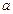
|
Нормальное 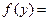
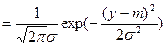
| 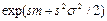
| 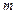
| 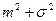
| 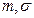
|
Бета-распределение 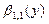 (равномерное) на отрезке (равномерное) на отрезке 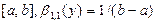
| 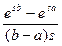
| 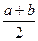
| 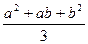
| 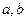
|
Бета-распределение 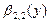 на отрезке на отрезке 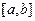 , ,
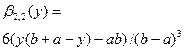
| 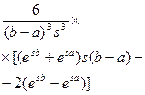
| 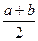 
| 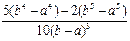
| 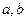
|
5.4.3 Вычисление W-функций для типовых соединений дуг
Использование W-функций позволяет вычислять вероятностные характеристики системы, содержащей множество дуг. Для этого необходимо уметь вычислять W-функции для трех типовых соединений:
· последовательное соединение дуг;
· параллельное соединение дуг;
· встречно-параллельное соединение двух дуг, или соединение обратной связью (иногда говорят – петля).
Рассмотрим эти случаи.
Дата добавления: 2016-09-06; просмотров: 1664;











