ЗНАКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ



знаки синуса знаки косинуса знаки тангенса и котангенса
Рассмотрим конкретный пример. Рассмотрим дуги в 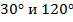 и, соответственно,
и, соответственно, 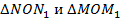 (рис. 1).
(рис. 1).
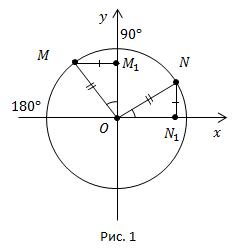
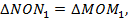 как прямоугольные по гипотенузе и острому углу
как прямоугольные по гипотенузе и острому углу 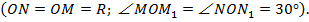
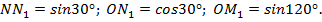
Из равенства треугольников следует равенство соответствующих сторон.
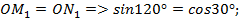
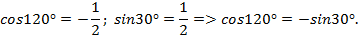
Функции большего угла приведены к функциям меньшего угла. В этом суть формул приведения.
Для применения формул приведения тригонометрическую функцию любого угла нужно привести к одному из видов: 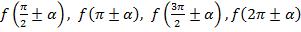 .
.
Формул приведения много, но все они подчиняются двум правилам:
Первое правило:
Для аргументов 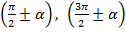 функция меняется на кофункцию, т.е. синус на косинус и наоборот, тангенс на котангенс и наоборот.
функция меняется на кофункцию, т.е. синус на косинус и наоборот, тангенс на котангенс и наоборот.
Для аргументов 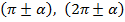 функция не меняется.
функция не меняется.
Примеры на первое правило:
Знак пока не учитываем, он определяется вторым правилом, пока важно понять, в каких случаях функция меняется на кофункцию, а в каких не меняется.
1) 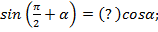
2) 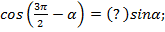
3) 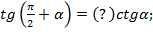
4) 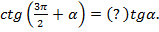
Для аргументов вида 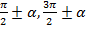 наименование функции следует изменить на кофункцию.
наименование функции следует изменить на кофункцию.
5) 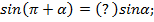
6) 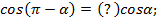
7) 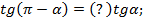
8) 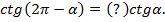
Для аргументов вида 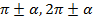 наименование функции не меняется.
наименование функции не меняется.
Второе правило (для знака приведенной функции, функции угла 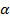 ).
).
1) Считаем угол 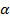 острым,
острым, 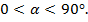
2) Определяем четверть и знак в ней приводимой функции (функции слева).
3) Ставим этот знак перед приведенной к углу 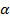 функцией (функцией справа).
функцией (функцией справа).
Примечание: Угол 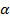 может быть любым, острым мы его считаем условно, для применения правила.
может быть любым, острым мы его считаем условно, для применения правила.
Примеры на второе правило:
1) 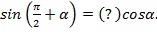
Рис. 2.
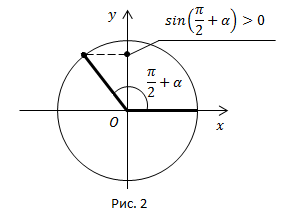
Угол 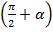 находится во второй четверти. Во второй четверти
находится во второй четверти. Во второй четверти 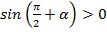 , ставим знак плюс.
, ставим знак плюс.
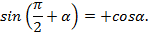
2) 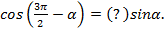
Рис 
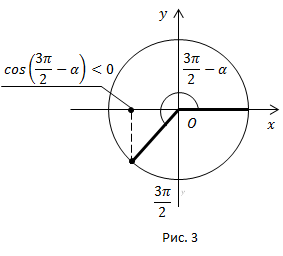
Угол 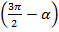 находится в третьей четверти. В третьей четверти
находится в третьей четверти. В третьей четверти 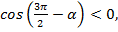 ставим знак минус.
ставим знак минус.
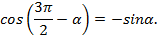
3) 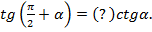
Рис. 4.
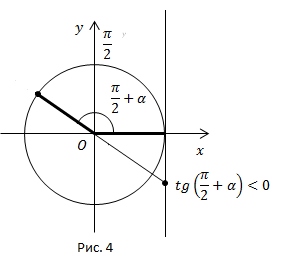
Угол 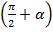 находится во второй четверти. Во второй четверти
находится во второй четверти. Во второй четверти 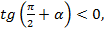 ставим знак минус.
ставим знак минус.
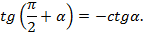
4) 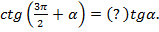
Рис. 5.
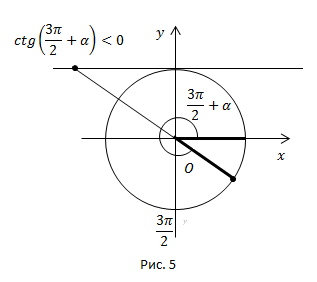
Угол 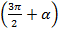 находится в четвёртой четверти. В четвёртой четверти
находится в четвёртой четверти. В четвёртой четверти 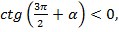 ставим знак минус.
ставим знак минус.
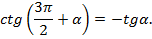
5) 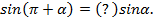
Рис. 6.
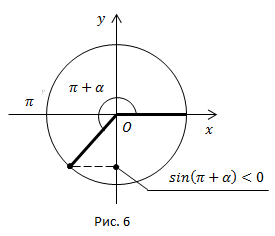
Угол 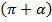 находится в третьей четверти. В третьей четверти
находится в третьей четверти. В третьей четверти 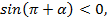 ставим знак минус.
ставим знак минус.
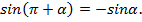
6) 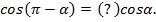
Рис. 7.
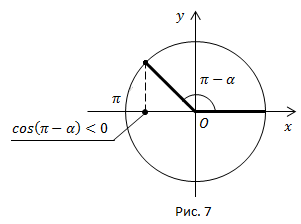
Угол 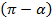 находится во второй четверти, во второй четверти
находится во второй четверти, во второй четверти 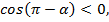 ставим знак минус.
ставим знак минус.
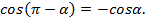
7) 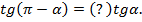
Рис. 8.
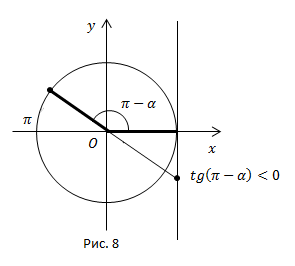
Угол 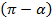 находится во второй четверти. Во второй четверти
находится во второй четверти. Во второй четверти 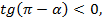 ставим знак минус.
ставим знак минус.
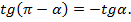
8) 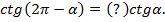
Рис. 9.
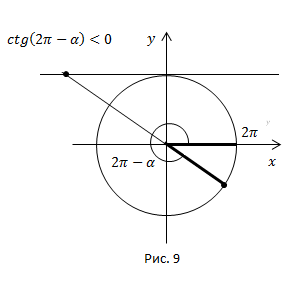
Угол 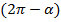 находится в четвёртой четверти. В четвёртой четверти
находится в четвёртой четверти. В четвёртой четверти 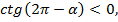 ставим знак минус.
ставим знак минус.
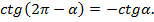
Итак, мы рассмотрели различные примеры применения первого и второго правил формул приведения.
Рассмотрим приемы, облегчающие запоминание формул приведения.
1. «Правило лошади». Глядя на числовую окружность легко ответить на вопрос, меняется ли функция на кофункцию.
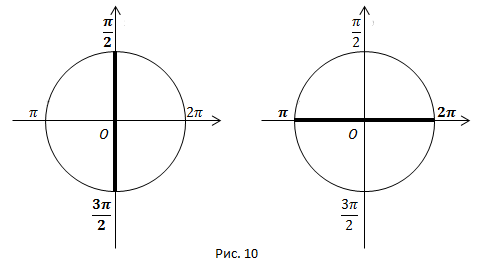
Для аргументов 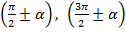 , т.е. аргументов, отложенных от вертикальной оси, на вопрос, меняется ли функция на кофункцию, лошадь, глядя на точки
, т.е. аргументов, отложенных от вертикальной оси, на вопрос, меняется ли функция на кофункцию, лошадь, глядя на точки 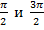 , будет утвердительно кивать – функция меняется на кофункцию (рис. 10) .
, будет утвердительно кивать – функция меняется на кофункцию (рис. 10) .
Для аргументов 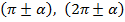 , т.е. аргументов, отложенных от горизонтальной оси, лошадь, глядя на точки
, т.е. аргументов, отложенных от горизонтальной оси, лошадь, глядя на точки 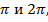 будет отрицательно мотать головой – функция не меняется (рис. 10) .
будет отрицательно мотать головой – функция не меняется (рис. 10) .
2. Используем периодичность и четность.
Вспомним, что наименьший положительный период у тангенса и котангенса равен 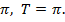 Это значит, что
Это значит, что
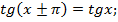
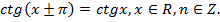
Например, 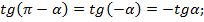
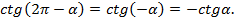
У синуса и косинуса наименьший положительный период равен 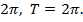
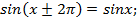
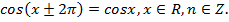
Например, 
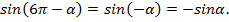
Рассмотрим примеры на использование формул приведения.
1) Вычислить значения всех тригонометрических функций для 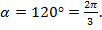
Решение (рис. 11).
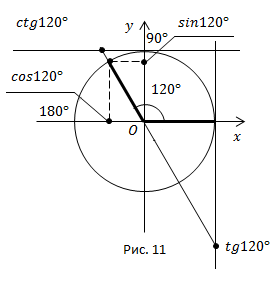
Угол 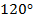 находится во второй четверти, синус в этой четверти положителен, косинус, тангенс и котангенс отрицательны.
находится во второй четверти, синус в этой четверти положителен, косинус, тангенс и котангенс отрицательны.
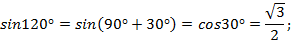
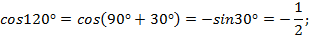
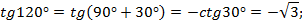
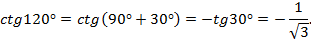
2) Вычислить значения всех тригонометрических функций угла 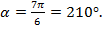
Решение (рис. 12).
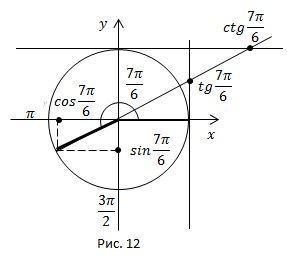
Угол 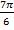 находится в третьей четверти, в третьей четверти синус и косинус отрицательны, тангенс и котангенс положительны.
находится в третьей четверти, в третьей четверти синус и косинус отрицательны, тангенс и котангенс положительны.
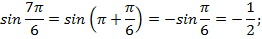
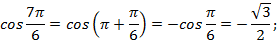
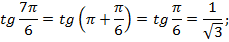
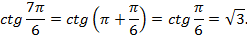
Дата добавления: 2016-06-05; просмотров: 3383;











