И результирующей устойчивости

Рассмотрим простейшую электрическую систему, расчетная схема и схемы замещения которой представлены на рис. 1.3, 1.5, а угловая характеристика мощности 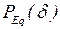согласно выражению (2.31) изображена на рис. 2.4.

Как известно, изменение мощности, отдаваемой генератором, на станции осуществляется воздействием на регулирующие органы турбины. В исходном режиме мощность турбины уравновешивается мощностью генератора 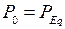, который вращается с неизменной частотой вращения. По мере открытия регулирующих клапанов (или направляющего аппарата гидравлических турбин) мощность турбины возрастает и равновесие вращающего и тормозящего моментов турбины и генератора нарушается, что вызывает ускорение его вращения.

При ускорении генератора вектор ЭДС 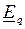перемещается относительно вращающегося с неизменной угловой скоростью 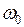вектора напряжения приемной системы 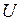. Связанное с этим увеличение угла 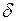и обуславливает согласно (2.31) соответствующее увеличение мощности генератора 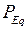, возрастающей до тех пор, пока она вновь не уравновесит увеличивающуюся мощность турбины. Таким образом, величиной непосредственно определяющей значение активной мощности, отдаваемой генератором приемнику, является угол 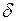. Угол 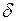представляет угол между ЭДС 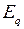, жестко связанным с поперечной осью ротора, и вектором напряжения системы .

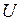Как вытекает из (2.31), зависимость мощности от 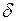имеет синусоидальный характер и, следовательно, с увеличением угла 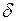мощность 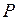сначала возрастает, а затем, достигнув максимального значения, начинает падать. При данном значении ЭДС 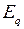и напряжении приемной системы 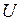существует определенный максимум передаваемой мощности:

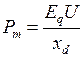, (2.37)

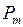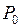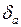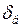который может быть назван идеальным пределом мощности рассматриваемой простейшей электрической системы. Равновесие между мощностью турбины и генератора достигается лишь при значениях мощности, меньших , причем данному значению мощности турбины соответствуют, вообще говоря, две возможные точки равновесия на характерные мощности генератора и, следовательно, два значения угла и (рис. 2.5). Однако в действительности устойчивый установившийся режим работы электропередачи возможен только при угле 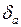. Режим, которому отвечает точка 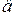на падающей части характеристики, неустойчив и длительно существовать не может.

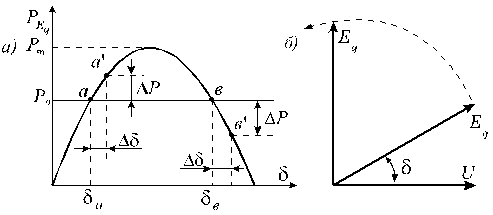
Рис. 2.5. Изменение мощности при приращениях угла (а),

выпадение из синхронизма (б)

Понятие о статической устойчивости.

Признаком устойчивости системы является такой характер изменения мощностей и моментов при небольшом отклонении от состояния равновесия, который вынуждает систему вновь возвращаться к исходному состоянию.

В режиме работы в точке 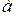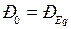. Если допустить, что угол 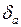получит небольшое приращение 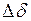, то мощность генератора, следуя синусоидальной зависимости от угла, также изменится на величину 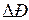, причем положительному 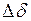соответствует положительной приращение 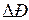. 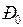не зависит от 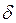и при любых углах остается одинаковой. Равновесие моментов генератора и турбины нарушается и на валу машины возникает избыточный момент тормозящего характера, поскольку тормозящий момент генератора в силу положительного изменения мощности 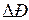преобладает над вращающим моментом турбины.

Под влиянием тормозящего момента ротор генератора начинает замедляться, что обуславливает перемещение связанного с ротором вектора ЭДС 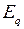в сторону уменьшения угла 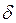, в результате чего вновь восстановится исходный режим в точке 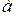. К тому же выводу можно прийти при отрицательном перемещении угла 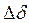в точке .

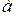Иной картина получается в точке 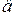. Здесь 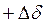соответствует 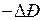генератора, которое вызовет появление избыточного момента ускоряющего характера ( 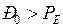в точке 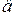), под влиянием которого 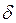не уменьшается, а возрастает. С ростом угла мощность генератора продолжает падать, что вызывает дальнейшее увеличение угла и т.д. Процесс сопровождается непрерывным перемещением вектора ЭДС 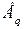относительно вектора системы 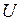и генератор выпадает из синхронизма. Таким образом, режим в точке 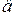статически неустойчив и практически не осуществим.

Под статической устойчивостью понимают способность системы самостоятельно восстанавливать исходный режим работы при малых возмущениях. Статическая устойчивость является необходимым условием существования установившегося режима работы системы. Точка 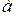и любая другая точка на восходящей характеристике отвечают статически устойчивым режимам и все точки на спадающей части - статически неустойчивым. Из этого вытекает формальный признак статической устойчивости системы: приращение угла 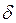и мощности генератора 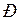должны иметь один и тот же знак, то есть 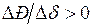или, переходя к пределу, - 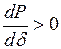. 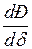носит название синхронизирующей мощности и, следовательно, критерием статической устойчивости системы в рассмотренных условиях является положительный знак синхронизирующей мощности. 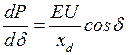положительна при 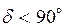. Критическим, с точки зрения устойчивости, при чисто индуктивной связи генератора с системой (рис. 2.6) является угол 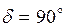, которому соответствует 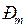. Зная 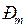, можно определить коэффициент запаса статической устойчивости :

.

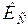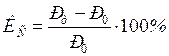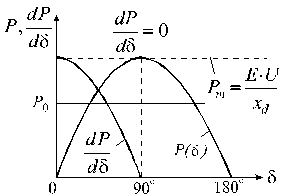
Рис. 2.6. Зависимость синхронизирующей мощности от угла

Понятие о динамической устойчивости.

Динамическая устойчивость связана с большими возмущениями - короткие замыкания, отключение или включение генераторов, линий передач, нагрузок, которые сопровождаются резкими изменениями характеристики мощности системы. Анализ характера процесса перехода системы от одного режима к другому требует учета инерционности машин и их реальных относительных перемещений. Вместо статической задачи приходится рассматривать задачу динамического перехода от одного режима к другому - динамическую устойчивость.

Под динамической устойчивостью понимают способность системы возвращаться после временного приложения больших возмущений к такому установившемуся режиму, при котором значения параметров режима в ее узловых точках близки к нормальным значениям.

Рассмотрим качания роторов генераторов и условия динамической устойчивости электропередачи при отключении одной из двух цепей линии (рис. 2.7).

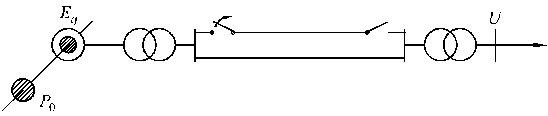
Рис. 2.7. Схема электропередачи при отключении цепи

В каждом режиме мощность электропередачи при постоянстве ЭДС 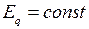и напряжения 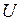определится по формуле

.

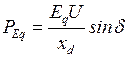При отключении цепи линии сопротивление передачи 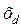возрастает и амплитуда характеристики мощности II уменьшится. В момент отключения цепи линии угол 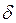мгновенно измениться не может и, следовательно, новый режим будет соответствовать точке 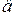на характеристике II (рис. 2.8). Избыточная мощность 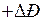вызывает ускорение машины и соответственно увеличение угла 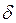. В точке 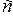мощность уравновешивается ( 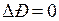), однако ротор, накопив относительную угловую скорость, по инерции проходит точку 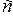. При дальнейшем росте угла мощность 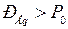, 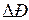меняет свой знак и начинает тормозить машину. В период торможения ротор возвращает запасенную кинетическую энергию, т.к. генератор должен покрыть большую мощность, чем он получает от первичного двигателя. Относительная скорость вращения 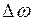уменьшается и в некоторой точке 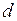вектор напряжения 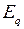вращается с той же скоростью, что и вектор напряжения 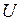. В дальнейшем угол 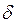начинает уменьшаться и процесс на характеристике мощности II протекает в обратном направлении к точке .

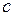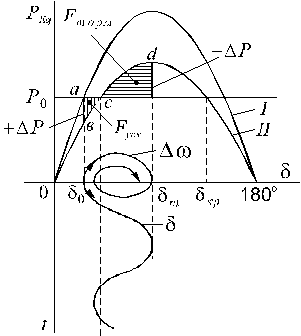
Рис. 2.8. Колебание мощности относительной угловой скорости и угла

при отключении одной цепи

Эту точку ротор вновь проходит по инерции и около точки 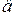угол 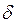достигает своего минимального значения, после чего вновь начинает возрастать. После постепенно затухающих колебаний в точке 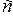установится новый стационарный режим с прежним значением передаваемой мощности .

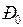Энергия ускорения и торможения ротора представлена на рис. 2.8 заштрихованными площадкам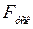и и 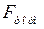. Максимальная возможная площадь торможения ограничивается верхней частью характеристики послеаварийного режима II и линией 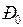до угла 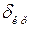. Если эта площадь меньше площади ускорения, то динамическая устойчивость не обеспечивается, причем процесс увеличения угла 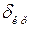быстро прогрессирует и машина выпадает из синхронизма. Отношение

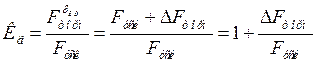
называют коэффициентом запаса динамической устойчивости, по величине и знаку которого можно судить об обеспечении динамической устойчивости при больших возмущениях.

Если 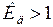, то динамическая устойчивость обеспечивается, при 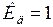- имеет место предельный по динамической устойчивости режим, при 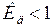- нарушение динамической устойчивости и выпадение генератора из синхронизма.

Понятие о результирующей устойчивости.

Под результирующей устойчивостью понимают способность системы бесперебойно снабжать основных потребителей электроэнергией, самостоятельно восстанавливать режим синхронной работы после нарушения устойчивости одного или нескольких генераторов, отдельных частей системы и перехода их на несинхронную работу.

Вхождение системы в синхронизм после непродолжительного времени асинхронного хода должно происходить под действием регуляторов скорости, возбуждения, ресинхронизаторов, АЧР, специальных тормозящих и нагрузочных устройств.