АНАЛИЗ СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ

(УСТОЙЧИВОСТИ В "МАЛОМ") ЭЛЕКТРИЧЕСКИХ

СИСТЕМ С ПОМОЩЬЮ ЛИНЕАРИЗОВАННЫХ

УРАВНЕНИЙ (МЕТОД МАЛЫХ КОЛЕБАНИЙ)

Общие положения

Метод малых колебаний является наиболее точным методом исследования электрических систем. Допуская небольшое возмущение исходного состояния составляют дифференциальные уравнения движения система и исследуют характер возникающих при этом так называемых свободных колебаний мощности и скорости.

При малых отклонениях параметров системы 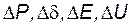и т.п. зависимости между ними во времени можно принять линейными и колебания машин системы описывается линейными дифференциальными уравнениями с постоянными коэффициентами, так называемыми линеаризованными уравнениями.

При принятом подходе к устойчивости ни природа возмущающих сил, ни величина не рассматриваются и они не участвуют в дифференциальных уравнениях. Анализ устойчивости сводится к выяснению характера изменения возмущений (отклонений), не определяя их величины. Математически мы имеем систему однородных дифференциальных уравнений, которые описывают свободные колебания и для суждения об устойчивости выясняют лишь характер возникающих колебаний, которые могут затухать или возрастать.

Электрическая система, включая генератор, возбудитель, регулятор возбуждения, ЛЭП и т.п., рассматривается как единый объект, устойчивость которого в целом должна быть обеспечена. Математическое описание (математическая модель) такой системы представляет взаимосвязанную систему дифференциальных и алгебраических уравнений, количество которых равно количеству независимых переменных.

Расчеты устойчивости "в малом" такой системы проводят в следующей последовательности.

1. Каждое уравнение системы представляют в виде исходного линеаризованного путем взятия полного дифференциала по всем переменным. Дифференцирование проводят в точке исходного режима. В общем виде можно записать:

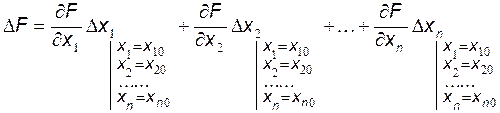. (138)

2. Из постоянных коэффициентов при переменных составляют главный (характеристический) определитель и приравнивают его к нулю ( ).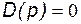

3. Раскрывая характеристический определитель, получают характеристическое уравнение, с помощью которого проводят исследование системы на устойчивость.

Вышеизложенное рассмотрим на примере простейшей электрической системы.

7.2. Исследование статической устойчивости простейшей системы с АРВ

Схема рассматриваемой системы представлена на рисунке 3. Переходные процессы в такой системе описываются уравнением переходных процессов в обмотке возбуждения и уравнением движения при замене моментов мощностями (1):

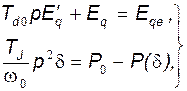(139)

где 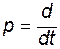- оператор (символ) дифференцирования.

Линеаризованные уравнения (139) имеют вид:

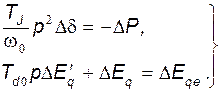(140)

Изменение вынужденной ЭДС 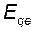на величину 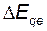обусловлено возбуждением и определяется законом регулирования и параметрами АРВ. Математически это выражается формулой:

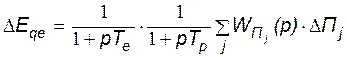, (141)

где 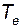- постоянная времени силового элемента (например, обмотки возбуждения возбудителя);

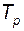- постоянная времени измерительного элемента АРВ;

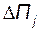- параметр регулирования;

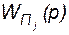- передаточная функция АРВ по параметру .

Выше было отмечено, что генератора могут быть снабжены АРВ пропорционального действия (АРВ п.д.) - регулирование по отклонению регулируемого параметра, и АРВ сильного действия (АРВ с.д.) - регулирование по отклонению, по скорости отклонения (по производным) и по ускорению отклонения (по вторым производным) регулируемого параметра. АРВ п.д. и АРВ с.д. различаются передаточными функциями и параметрами. В некоторой идеализации их передаточные функции записываются соответственно как:

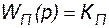, (142)

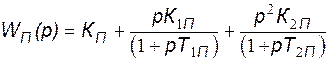, (143)

где 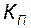- коэффициент усиления по отклонению;

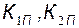- коэффициенты усиления по производным;

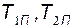- постоянные времени дифференцирующих элементов АРВ.

В качестве режимных параметров в АРВ п.д. используются либо напряжение и ток статора (системы компаундирования с корректором напряжения), либо только напряжение генератора.

В АРВ с.д. используются напряжение генератора, ток статора, частота генератора, угол по электропередаче, иногда дополнительно - ток ротора.

Подставляя (142) или (143) в (141) и далее в (140), получаем соответствующий тип АРВ для генератора.

Рассмотрим получение характеристического уравнения рассматриваемой системы с АРВ п.д. и в качестве режимного параметра примем отклонение напряжения на зажимах генератора 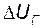. Тогда (141) имеет вид:

.

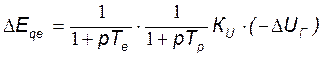Для упрощения расчетов примем 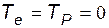. Окончательно систему (140) запишем в виде:

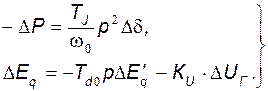(144)

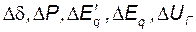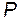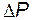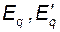В (144) пять неизвестных ( ) и для решения необходимо дополнить еще тремя уравнениями. Недостающие уравнения получим путем представления мощности , а, следовательно, и через и 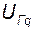. Мощности через эти ЭДС и напряжение определяется по (31), (32) и (33). Отсюда согласно (138) имеем:

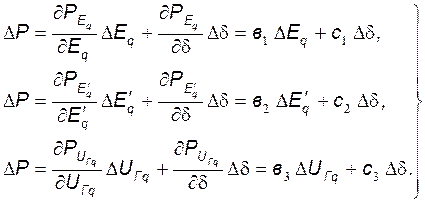(145)

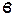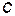Коэффициенты и определяются как частные производные выражений мощности (31)¸(33):

,

,

,

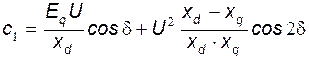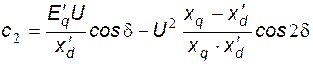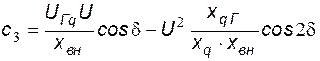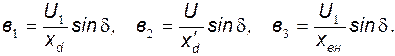
В последних выражениях 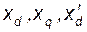включают в себя внутренние сопротивления генератора и внешней цепи.

Подставляя выражения 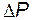из (145) в (144) после преобразований и приняв 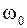= 1, получим:

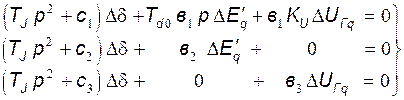(146)

Определитель системы (146)

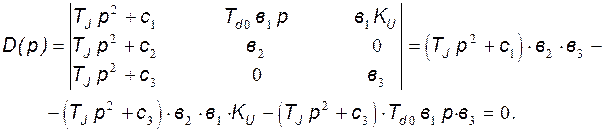
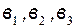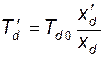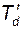Подставляя значения и выражая , где - постоянная времени обмотки возбуждения при закороченном статоре, получим:

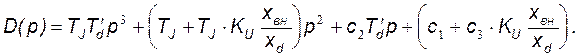
Согласно последнему выражению получим характеристическое уравнение вида:

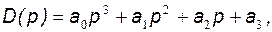(147)

где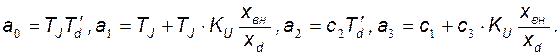

В зависимости от детализации рассматриваемой системы (числа машин, закона регулирования возбуждения, демпфирования и т.п.) порядок (степень оператора 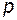) может быть выше.

В общем виде уравнение (147) имеет вид:

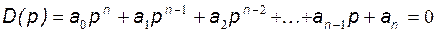. (148)

Зная характеристическое уравнение системы, можно решить задачу об устойчивости - о затухании или возрастании свободных колебаний системы.

Как показал Ляпунов А.М., судить об устойчивости системы можно по знаку вещественной части корней характеристического уравнения.

Теоремы А.М. Ляпунова.

1. Если характеристическое уравнение имеет корни только с отрицательными вещественными частями, то система устойчива "в малом", т.е. при малых изменениях режима системы.

2. Когда между корнями характеристического уравнения находятся такие корни, вещественные части которых положительны, система неустойчива.

Однако, определение корней характеристического уравнения представляет затруднения, т.к. порядок уравнения, как правило, высок - 5-й, 6-й и выше. На практике применяются различные способы определения характера корней уравнения (расположения на комплексной плоскости) без непосредственного его решения. Это критерии Гурвица, Рауса, Михайлова, метод 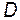-разбиений и т.п.

7.3. Пример исследования системы по корням

характеристического уравнения

Рассмотрим простейшую нерегулируемую систему ( 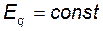) и не учитываем переходный электромагнитный процесс. В этом случае состояние системы описывается уравнением движения:

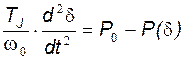, где .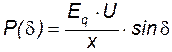

Имеем одну переменную - .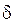

Линеаризованное уравнение имеет вид:

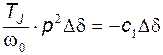, где .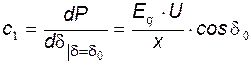

Характеристическое уравнение, определяемое выражением

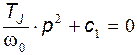
имеет корни .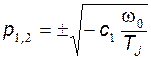

Если 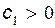, то корни получаются чисто мнимыми, а если 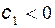, то чисто вещественные.

В случае мнимых корней

,

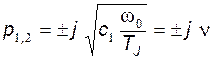где 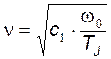- собственная частота колебаний ротора.

Период колебаний 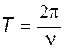. Решение имеет вид:

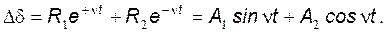
Изменение угла происходит по закону незатухающих синусоидальных колебаний около 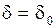(рисунок 59,а). При учете демпфирования колебания затухают, т.е. система устойчива.

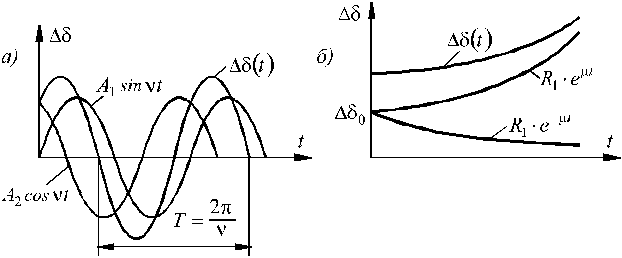
Рисунок 59 - Устойчивый (а) и неустойчивый (б) процессы в зависимости

от знака вещественной части корней характеристического уравнения

В случае вещественных корней:

.

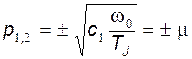Изменение угла имеет апериодический характер (рисунок 59,б):

.

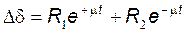Наличие положительного вещественного корня приводит к прогрессирующему увеличению 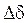и система оказывается неустойчивой.

Таким образом, наличие комплексных корней с положительной вещественной частью характеризует самораскачивание системы, т.е. колебание системы с нарастающей амплитудой.