СТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ. ПРАКТИЧЕСКИЕ

КРИТЕРИИ ОЦЕНКИ СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ

ЭЛЕКТРИЧЕСКОЙ СИСТЕМЫ

Общие положения

Известно, что установившийся режим системы может быть устойчивым и неустойчивым. В электрической системе, называемой статически неустойчивой, малые возмущения приводят к изменению параметров ее режима, которые в начале процесса происходят медленно в виде самопроизвольного изменения, или, как иначе называют сползания, или текучести, параметров нормального режима системы.

Для электрической системы (рис. 3.1), где два генератора (станции) питают общую нагрузку, установившийся режим определяется общими зависимостями, которые могут быть выражены аналитически или представлены графически:

, (3.1)

где 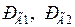- активные мощности, отдаваемые первой и второй генераторными станциями;

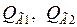- соответствующие реактивные мощности;

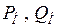- активная и реактивная мощности в узле нагрузки.

Рис. 3.1. Схема исследуемой системы

Изменение активной и реактивной мощности каждого из генераторов и нагрузки покажем на примере системы, изображенной на рис. 3.1. Отказавшись от допущения 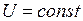и заметим, что теперь отклонение режима может вызываться изменением мощности одной из турбин, изменением активной или реактивной мощности нагрузки или одновременным действием всех этих факторов. Предполагая последнее, запишем уравнения моментов на валах генераторов и два уравнения баланса мощности при отклонении режима:

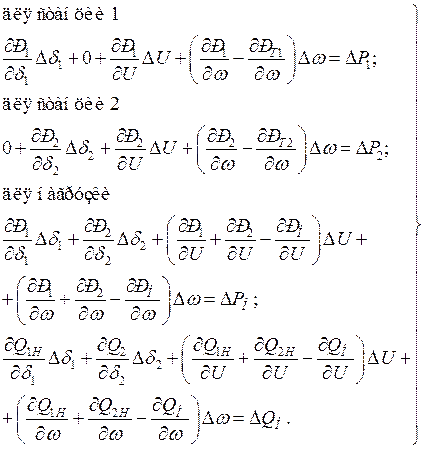
(3.2)

Здесь значения 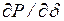; ; 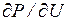; 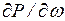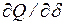и т.д., являющиеся коэффициентами при отклонениях параметров режима ( 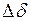, , 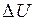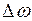), рассматриваются при малых отклонениях этих параметров как постоянные величины. Полагая, что значения 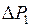, , 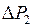, 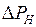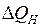известны, с помощью системы уравнений (3.2) легко найти любое из указанных выше отклонений параметров режима, то есть 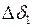, , 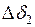, 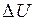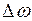. Например,

.

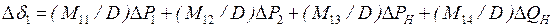Здесь 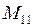, , 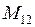, 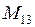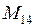- соответствующие миноры системы уравнений (3.2);

D – главный определитель системы уравнений (3.2):

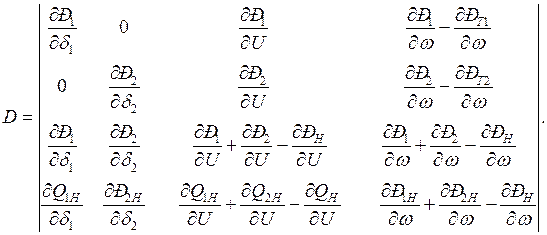
Аналогично тому, как определялось 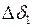, могут быть найдены значения 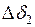, , 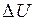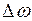. Если при не равных нулю минорах М определитель D окажется равным нулю, то это будет означать, что любое очень малое отклонение величин 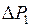, , 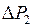, 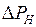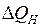(всех или какой-либо одной) может вызвать неограниченно большие изменения параметров режима 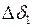, , 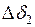, , 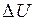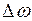то есть практически режим будет неустойчивым. Он будет иметь тенденцию к «текучести», параметры режима будут самопроизвольно уползать от своих исходных значений. Критерием, указывающим на критический режим, будет условие

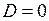. (3.3)

Принятый здесь подход к анализу является приближенным уже потому, что в нем выявляется только тенденция системы к неустойчивости, без учета характера движения, зависящего от инерционных постоянных системы. Практические критерии, таким образом, выявляют только текучесть режима (сползание), или апериодическую неустойчивость, не выявляя той неустойчивости, которая может проявляться в виде колебаний – колебательной неустойчивости (самораскачивания).

Принимая на основе практических соображений ряд дальнейших ограничений (допуская, например, постоянство тех или иных параметров режима), из условия 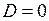получим частные критерии, то есть критерии, действующие при тех или иных ограничениях, в том числе и уже полученные выше. Так, при постоянстве частоты в системе ( 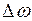= 0), постоянстве напряжения в узловой точке ( 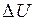= 0) и постоянстве мощности турбин ( 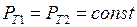) критический по устойчивости режим наступит при

,

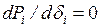где 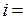1, 2 и т.д.

Это очевидно из первого и второго уравнений (3.2), которые дают:

; .

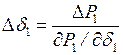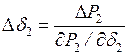При постоянстве частоты ( 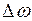= 0) и сохранении баланса активной мощности в узле нагрузки ( 0) условием критического по устойчивости режима будет

.

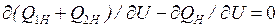Обозначая 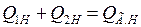и учитывая, что дифференцирование происходит только по одной переменной, запишем

,

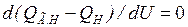или

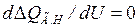. (3.4)