В простейшей системе

Получим выражения электромагнитной мощности генератора 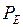при различных известных режимных параметрах простейшей системы: через синхронную ЭДС 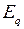, поперечную составляющую переходной ЭДС 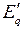, поперечную составляющую напряжения на зажимах генератора 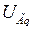. При всех случаях напряжение системы принимаем равным 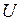и для каждого случая электромагнитную активную мощность генератора обозначим соответственно , .

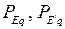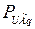Из векторной диаграммы (рис. 2.3) имеем две подсистемы уравнений I и II:

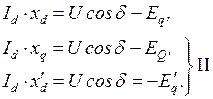(2.27)

Выражение электромагнитной мощности через 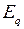и .

И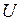з подсистемы I имеем:

,

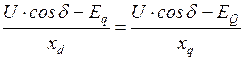откуда

.

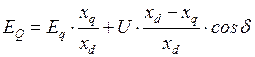Последнее выражение для 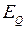и значение тока 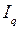из (2.7) подставим в (2.22), получим выражение для активной электромагнитной мощности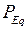

.

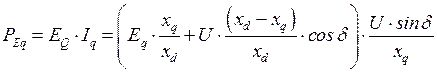После преобразований окончательно получим

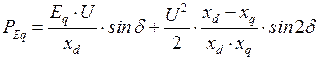. (2.28)

Выражение электромагнитной мощности через 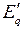и .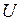

Из подсистемы II имеем:

,

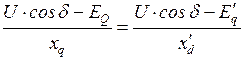откуда

.

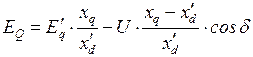Поступая аналогично, как и для 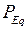, получим

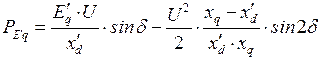. (2.29)

Выражение (2.29) называют динамической характеристикой мощности и используют при расчетах динамической устойчивости простейшей системы.

Выражение электромагнитной мощности через 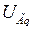и .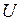

Согласно (2) .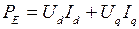

Подставив в последнее выражение значения составляющих токов и напряжений, получаемых из векторной диаграммы (рис. 2.3),

,

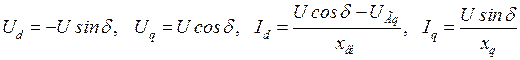получим выражение для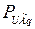

.

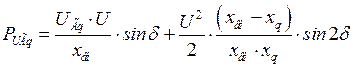Напомним, что в последнем выражении и выше согласно рис. 1.3 и 1.4 обозначено:

, , , .

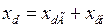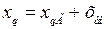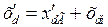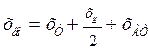С учетом этого

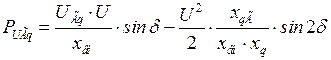. (2.30)

В формулах (2.28)-(2.30) электромагнитная мощность генератора имеет 2 слагаемых. В обычных условиях при достаточно высоких ЭДС амплитуда 2-й гармоники (2-е слагаемое) составляет 10-15 %, является причиной явнополюсности и свойственна только для машин с явновыраженными полюсами (гидрогенераторы). В выражениях для мощности турбогенератора, у которого 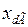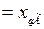, 2-я гармоника отсутствует.

В инженерных расчетах часто не учитывают второе слагаемое в (2.28)-(2.30). Кроме того, вместо ЭДС 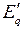и напряжение 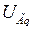принимают 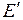и 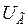, которые легко определить по (2.11) и (2.13). В результате таких допущений выражения электромагнитной мощности генератора, записанные через различные режимные параметры, значительно упрощаются:

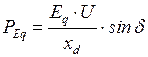, (2.31)

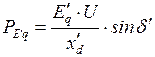, (2.32)

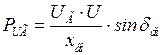. (2.33)

Определение реактивной мощности, отдаваемой генератором.

Рассмотрим неявнополюсную машину, для которой 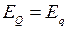. Согласно (2.23) .

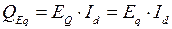После подстановки в последнее выражение значения тока 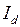, получаемого из векторной диаграммы и равного 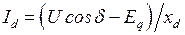, определим значение внутренней реактивной мощности генератора 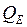, то есть мощности, которая протекает в схеме замещения в начале ветви с сопротивлением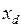

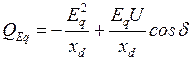. (2.34)

Выражение (2.34) получено в случае записи комплекса полной мощности в виде 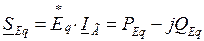. Здесь составляющая полного тока генератора 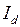опережает вектор ЭДС 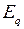(см. векторную диаграмму) на угол 90°. В расчетах при принятом направлении осе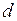й и .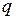

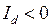При представлении комплекса полной (кажущейся) мощности генератора 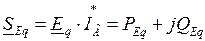. После подстановки составляющей тока 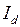, которая в этом случае отстает от вектора ЭДС 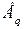на 90° и равна 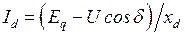, из выражения (2.23) получим

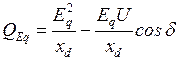. (2.35)

Последняя формула, как и (2.34), используется в расчетах реактивной мощности, выдаваемой генератором, для простейшей системы. Составляющая тока .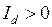

Выражение для 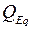можно получить и в функции угла 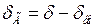, подставив 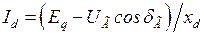в (2.23). При этом

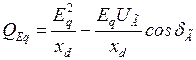. (2.36)

На рис. 2.4 показаны характеристики активной и реактивной мощностей генератора простейшей системы в функции угла 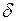. Характеристики получены по выражениям (2.31) и (2.35). Такие характеристики иногда называют угловыми характеристиками мощности. Графики (рис. 2.4) построены при условии 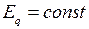применительно к неявнополюсным генераторам. Постоянство ЭДС 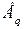означает, что генератор (эквивалентный генератор) работает при неизменном токе возбуждения. Такой случай не отвечает реальным условиям, однако его анализ целесообразен для более полного представления об условиях работы системы.

Рис. 2.4. Угловые характеристики мощностей генератора

Графики, показанные на рис. 2.4, позволяют сделать следующие выводы.

1. При неизменной ЭДС изменение активной мощности генераторов определяется только углом .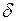

2. В рассматриваемом идеализированном случае (при отсутствии активных сопротивлений и проводимостей) нулевому значению угла 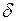активная мощность, также равная нулю.

3. Увеличение угла 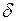приводит к росту активной мощности, который ограничивается, однако, некоторым предельным значением 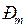, имеющим место при .

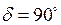4. Каждому значению передаваемой активной мощности соответствует вполне определенная реактивная мощность генератора.

Мощность, определяемая в соответствии с рис. 2.4 как амплитуда угловой характеристики 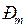, называется пределом мощности. Этот предел ограничивается пропускной способностью электропередачи между удаленным генератором (станцией) и приемной системой.

Активная мощность генератора определяется мощностью, которую развивает турбина, приводящая этот генератор во вращение. Поэтому для того, чтобы установить параметры того или иного режима, необходимо поставить во взаимное соответствие характеристики генератора и турбины. Первая определяется применительно к простейшей системе характеристикой 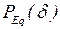. Для каждого установившегося режима системы мощность турбины может считаться заданной величиной. Поэтому в принятых координатах и допущениях (п. 1.2) характеристика мощности турбины 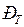(иногда обозначают 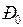) имеет вид прямой, параллельной оси абсцисс (рис. 2.4), то есть .

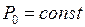В установившемся режиме работы мощность, развиваемая турбиной, равна активной мощности генератора. Поэтому пересечение соответствующих характеристик определяет тот угол 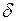, который отвечает заданной мощности. Этот угол позволяет найти соответствующую рассматриваемому режиму внутреннюю реактивную мощности 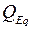и мощность 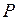в начале и конце передачи.