Уравнение теплопроводности.

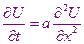
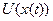- температура в точке с координатой 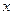в момент времени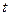

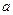- коэффициент теплопроводности.

Любое уравнение параболического типа с постоянными коэффициентами путем соответствующих преобразований (поворотом системы координат в пространстве 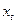и изменением начала координат) может быть приведено к следующему виду:

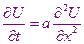- каноническая форма уравнения параболического типа.

Уравнение теплопроводности - параболическое уравнение. Для его решения необходимо дополнить начальными и граничными условиями.

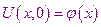- задает распределение температуры в начальный момент времени.

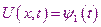- температура на левой границе

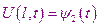- температура на правой границе

Граничные условия могут иметь и другой вид они могут накладывать ограничение на производную.

Численное решение поставленной задачи основано на введение разностной сетки в области решения задачи. Значение производных, начальные и граничные условия выражаются через значения функций 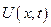в узлах сетки, в результате чего получается система алгебраических уравнений, называемая разностной схемой. Решая эту систему можно найти значение искомой функции в узлах сетки. Построение разностной схемы начинается с введения сетки в рассмотренную область пространства. Наиболее простыми и самыми распространенными являются прямоугольные сетки. Например, для решения задачи можно построить прямоугольную разностную сетку с шагом по координате 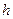и шагом по времени .

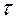Можно использовать сетки с неравномерным шагом и даже не прямоугольные сетки. Все зависит от конкретных условий задачи.

Коэффициенты узлов сетки имеют значения:

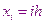
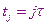
Этот узел будем обозначать .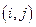

Значение искомой функции в узле 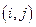обозначим 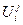. Совокупность этих значений образует сеточную функцию, которая аппроксимирует значение температуры в узлах сетки.

При построении конечно-разностной схемы используется некоторый шаблон, показывающий расположение смежных узлов в двух или более слоях, которые используют при аппроксимации производных конечно-разностными соотношениями. При построении конечно-разностной схемы может использоваться следующий шаблон.

Метод 35