Метод конечных разностей (МКР) (метод сеток).

Одним из универсальных методов решения краевых задач является метод конечных разностей.

Рассмотрим применение МКР для решения линейного дифференциального уравнения второго порядка.

Пусть требуется найти дифференциальное уравнение:

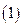
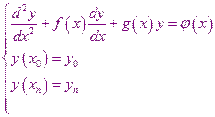заданы краевые условия

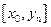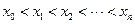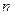Разбиваем отрезок узловыми равноотстоящими точками на частных отрезков. В каждой внутренней узловой точке аппроксимируем, производные с помощью разностных соотношений и записываем решаемое дифференциальное уравнение (1) для каждой внутренней узловой точки. В результате получается система алгебраических уравнений для нахождения неизвестных значений функции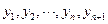

Рассмотрим узловую точку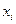

Аппроксимируем решаемое дифференциальное уравнение для узловой точки 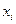. Для этого

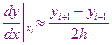
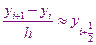
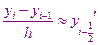
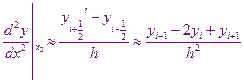получили приблизительное значение производной.

Подставим найденные значения 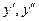в дифференциальное уравнение. Найдем, что в узле 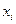дифференциальное уравнение приблизительно заменяется следующим алгебраическим уравнением:

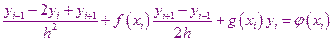
Аналогичное соотношение можно записать для каждого внутреннего узла. В результате получается система линейных алгебраических уравнений; число этих уравнений равно числу неизвестных значений 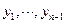, решаем систему и находим неизвестные.

Замечание: полученная система СЛАУ имеет трехдиагональную матрицу, поэтому решать полученную систему удобно с помощью метода прогонки.

Тема №8