Волновое уравнение.
Одним из наиболее распространенных в инженерной практике уравнений с частными производными второго порядка является волновое уравнение, описывающее различные виды колебаний. Поскольку колебания — процесс нестационарный, то одной из независимых переменных является время t. Кроме того, независимыми переменными в уравнении являются также пространственные координаты х, у, z. В зависимости от их количества различают одномерное, двумерное и трехмерное волновые уравнения.
Одномерное волновое уравнение описывает продольные колебания стержня, сечения которого совершают плоскопараллельные колебательные движения, а также поперечные колебания тонкого стержня и другие задачи. Двумерное волновое уравнениеиспользуется для исследования колебаний тонкой пластины. Трехмерное волновое уравнениеописывает распространение волн в пространстве.
Рассмотрим одномерное волновое уравнение, которое можно записать в виде

Для поперечных колебаний струны искомая функция U(x,t) описывает положение струны в момент t. В этом случае 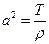 , где Т — натяжение струны,
, где Т — натяжение струны, 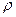 — ее линейная плотность. Уравнение записано для случая свободных колебаний. Сопротивление среды колебательному процессу не учитывается.
— ее линейная плотность. Уравнение записано для случая свободных колебаний. Сопротивление среды колебательному процессу не учитывается.

Решим задачу Коши для этого уравнения. Вот условия задачи:

Эти условия описывают начальную форму струны 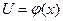 и скорость ее точек.
и скорость ее точек.
На практике чаще приходится решать не задачу Коши для бесконечной струны, а смешанную задачу для ограниченной струны некоторой длины 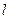 . В этом случае задают граничные условия на ее концах. В частности, при закрепленных концах их смещения равны нулю, и граничные условия имеют вид
. В этом случае задают граничные условия на ее концах. В частности, при закрепленных концах их смещения равны нулю, и граничные условия имеют вид

Для решения такой задачи используем явную трехслойную схему типа крест. Заменим в начальном уравнении вторые производные искомой функции U по t и х их конечно-разностными соотношениями с помощью значений сеточной функции 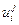 в узлах сетки
в узлах сетки 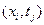
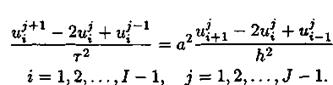
Отсюда можно найти явное выражение для значения сеточной функции на (j + 1)-м слое:
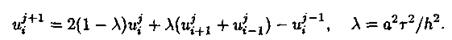
Здесь, как обычно в трехслойных схемах, для определения неизвестных значений на (j + 1)-м слое нужно знать решения на j-м и (j — 1)-м слоях. Поэтому начать счет можно лишь для второго слоя, а решения на нулевом и первом слоях должны быть известны. Они находятся с помощью начальных условий. На нулевом слое имеем
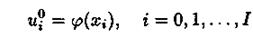
Для получения решения на первом слое воспользуемся вторым начальным условием. Производную 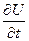 заменим конечно-разностной аппроксимацией.
заменим конечно-разностной аппроксимацией.
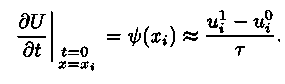
Из этого соотношения можно найти значения сеточной функции на первом временном слое:
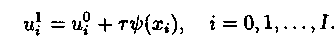
Отметим, что аппроксимация начального условия в таком виде ухудшает аппроксимацию исходной дифференциальной задачи: погрешность аппроксимации становится порядка 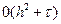 ,т. е. первого порядка по
,т. е. первого порядка по 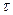 , хотя сама схема имеет второй порядок аппроксимации по h и
, хотя сама схема имеет второй порядок аппроксимации по h и 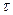 . Положение можно исправить, если взять более точное представление
. Положение можно исправить, если взять более точное представление
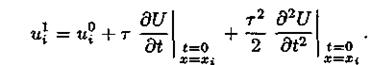
Так как,
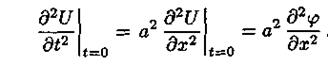
то:
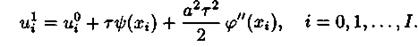
Теперь разностная схема обладает погрешностью аппроксимации порядка 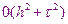 .
.
Рассмотренная разностная схема решения задачи условно устойчива. Необходимое и достаточное условие устойчивости имеет вид
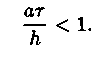
Следовательно, при выполнении этого условия и с учетом аппроксимации схема сходится к исходной задаче со скоростью 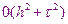 .
.
Уравнение Лапласа.
Многие стационарные физические задачи (исследования потенциальных течений жидкости, определение формы нагруженной мембраны, задачи теплопроводности и диффузии в стационарных случаях и др.) сводятся к решению уравнения Пуассонавида
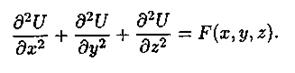
При F(x, у, z) = 0, уравнение Пуассона называют уравнением Лапласа.Для простоты будем рассматривать двумерное уравнение Лапласа
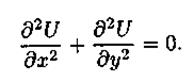
Решение этого уравнения будем искать для некоторой ограниченной области G изменения независимых переменных х, у. Границей области G является замкнутая линия L. Для полной формулировки краевой задачи кроме уравнения Лапласа нужно задать граничное условие на границе L.Примем его в виде

Задача, состоящая в решении уравнения Лапласа (или Пуассона) при заданных значениях искомой функции на границе расчетной области, называется задачей Дирихле.
Одним из способов решения стационарных эллиптических задач, в том числе и краевой задачи, является их сведение к решению некоторой фиктивной нестационарной задачи (гиперболической или параболической), найденное решение которой при достаточно больших значениях времени t близко к решению исходной задачи. Такой способ решения называется методом установления.
Поскольку решение U(x,y) уравнения Лапласа не зависит от времени, то можно в это уравнение добавить равный нулю (при точном решении) член 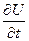 . Тогда уравнение примет вид
. Тогда уравнение примет вид
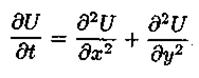
Это — известное нам уравнение теплопроводности, для которого мы уже строили разностные схемы. Остается только задать начальное условие. Его можно принять практически в произвольном виде, согласованном с граничными условиями. Положим
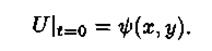
Граничное условие при этом остается стационарным, т. е. не зависящим от времени.
 Процесс численного решения такого уравнения
Процесс численного решения такого уравнения  состоит в переходе при
состоит в переходе при  от произвольного значения к искомому стационарному решению. Счет ведется до выхода решения на стационарный режим. Естественно, ограничиваются решением при некотором достаточно большом t, если искомые значения на двух последовательных слоях совпадают с заданной степенью точности.
от произвольного значения к искомому стационарному решению. Счет ведется до выхода решения на стационарный режим. Естественно, ограничиваются решением при некотором достаточно большом t, если искомые значения на двух последовательных слоях совпадают с заданной степенью точности.
Метод установления фактически представляет итерационный процесс, причем на каждой итерации значения искомой функции получаются путем численного решения
некоторой вспомогательной задачи. В теории разностных схем показано, что этот итерационный процесс сходится к решению исходной задачи, если такое стационарное решение существует.
Другой способ решения задачи Дирихле состоит в построении разностной схемы путем аппроксимации уравнения Лапласа. Введем в прямоугольной области G сетку с помощью координатных прямых х = const и у = const. Примем, для простоты значения шагов по переменным, х и у равными h (предполагается, что стороны области G соизмеримы). Значения функции U в узлах 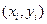 заменим значениями сеточной функции
заменим значениями сеточной функции 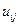 Тогда, аппроксимируя в уравнении Лапласа вторые производные с помощью отношений конечных разностей, получим разностное уравнение.
Тогда, аппроксимируя в уравнении Лапласа вторые производные с помощью отношений конечных разностей, получим разностное уравнение.
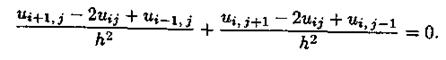
С помощью данного уравнения можно записать систему линейных алгебраических уравнений относительно значений сеточной функции в узлах в виде
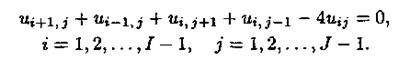
Значения сеточной функции в узлах, расположенных на границе расчетной области, могут быть найдены из граничного условия:
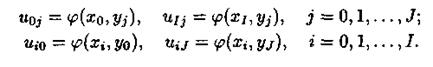
Перейдем теперь к решению полученной системы. Каждое уравнение системы (за исключением тех, которые соответствуют узлам, расположенным вблизи границ) содержит пять неизвестных. Одним из наиболее распространенных методов решения этой системы линейных уравнений является итерационный метод. Каждое из уравнений записываем в виде, разрешенном относительно значения 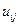 в центральном узле:
в центральном узле:
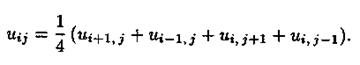
В ряде случаев уравнение с частными производными удобно привести к системе обыкновенных дифференциальных уравнений, в которых оставлены производные искомой функции лишь по одной переменной.
Такой способ можно использовать и для решения уравнения Лапласа. Пусть требуется решить для него задачу Дирихле в прямоугольнике ABCD. Разобьем прямоугольник на полосы с помощью прямых, параллельных  оси х. Для определенности проведем три отрезка
оси х. Для определенности проведем три отрезка  , которые разделят прямоугольник на четыре полосы постоянной ширины h. Решение U задачи Дирихле приближенно заменим набором функций
, которые разделят прямоугольник на четыре полосы постоянной ширины h. Решение U задачи Дирихле приближенно заменим набором функций 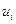 ,каждая из которых определена на отрезке U и зависит только от одной переменной х, т. е.
,каждая из которых определена на отрезке U и зависит только от одной переменной х, т. е. 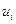 =
= 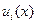 для
для 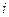 =1,2,3. На отрезках
=1,2,3. На отрезках 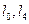 значения
значения 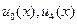 заданы граничными условиями.
заданы граничными условиями.
Построим разностную схему, для определения значений функций 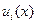 . Аппроксимируя в уравнении вторую производную по у,с помощью отношения конечных разностей, получаем
. Аппроксимируя в уравнении вторую производную по у,с помощью отношения конечных разностей, получаем
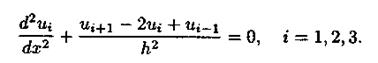
Таким образом, решение задачи Дирихле сводятся к решению краевой задачи для системы обыкновенных дифференциальных уравнений относительно значений искомой функции вдоль прямых 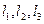 . В этом состоит метод прямых. Граничные условия при х=а, х = b можно получить из уравнений
. В этом состоит метод прямых. Граничные условия при х=а, х = b можно получить из уравнений
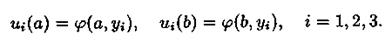
Метод прямых широко, используется для решения нестационарных задач. Например, если имеются две независимые переменные х, t, а искомый параметр является гладкой функцией переменной х, то дискретизация вводится по этой переменной. Тогда исходная задача заменяется задачей Коши для системы обыкновенных дифференциальных уравнений вида

Дата добавления: 2017-03-12; просмотров: 3641;











