Явная разностная схема для уравнения теплопроводности.

Используя шаблон для каждого внутреннего узла области решения апроксимируется уравнение теплопроводности

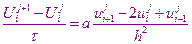
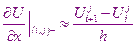
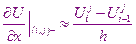
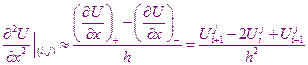
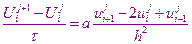
Отсюда найдем:

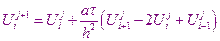
Используя начальные и граничные условия, находят значения сеточной функции во всех узлах на нулевом временном уровне.

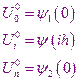
Затем с помощью соотношений

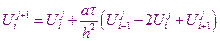
находятся значения этих функций во всех внутренних узлах на первом временном уровне, после чего находим значение на граничных узлах

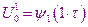
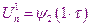
В результате мы находим значение функций во всех узлах на первом временном уровне. После этого с помощью этих соотношений находим все остальные значения и т.д.

В рассматриваемой разностной схеме значения искомой функции на следующем временном уровне находится непосредственно, явно с помощью формулы

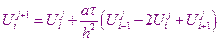
Поэтому рассматриваемая разностная схема, использующая этот шаблон, называется явной разностной схемой. Точность её имеет порядок .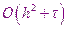

Данная разностная схема проста в использовании, однако она обладает существенным недостатком. Оказывается, что явная разностная схема обладает устойчивым решением только в том случае, если выполняется условие:

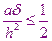
Явная разностная схема является условно устойчивой. Если условие не выполняется, то небольшие погрешности вычислений, например, связанные с округлением данных компьютера приводит к резкому изменению решения. Решение становится неприемлемым для использования. Это условие накладывает весьма жесткие ограничения на шаг по времени, что может оказаться неприемлемым из-за значительного увеличения времени счета решения этой задачи.

Рассмотрим разностную схему, использующую другой шаблон

Метод 36