Транспортная задача.
Автобаза обслуживает три магазина, доставляя в них товары из двух торговых баз. Известно, что ежедневно вывозится с первой базы 12т. товара, а со второй базы 15т. При этом в магазины ежедневно завозится в первый – 8т., во второй 9т., в третий 10т. Стоимость перевозки одной тонны определяется таблицей.
| База | Магазин | ||
| 0,80 | 1,1 | 0,90 | |
| 1,00 | 0,70 | 1,20 |
Требуется спланировать перевозки так, чтобы их стоимость была минимальной.
Введём переменные величины, 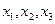 соответствующие количеству товара доставляемого в первый, второй и третий магазины соответственно;
соответствующие количеству товара доставляемого в первый, второй и третий магазины соответственно; 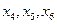 - количество товара поставляемого со второй базы. Стоимость перевозок запишем в виде:
- количество товара поставляемого со второй базы. Стоимость перевозок запишем в виде:
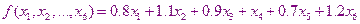 - это и есть целевая функция.
- это и есть целевая функция.
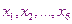 - проектные параметры. На проектные параметры накладываются ограничения. Во-первых, это ограничение равенства, оно следует из условия задачи и описывает количество товаров, которые вывозят с баз и доставляют в магазины.
- проектные параметры. На проектные параметры накладываются ограничения. Во-первых, это ограничение равенства, оно следует из условия задачи и описывает количество товаров, которые вывозят с баз и доставляют в магазины.

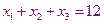
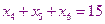
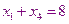
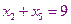
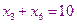
К данной системе необходимо добавить систему неравенств
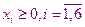 . В этой системе равенств независимыми являются только четыре уравнения, поэтому из шести независимых
. В этой системе равенств независимыми являются только четыре уравнения, поэтому из шести независимых 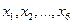 фактически независимыми являются только две переменные
фактически независимыми являются только две переменные 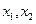 . Тогда ограничения, налаживаемые на переменные можно записать как
. Тогда ограничения, налаживаемые на переменные можно записать как

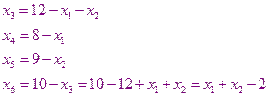
А целевая функция 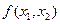 принимает вид
принимает вид 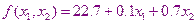 . Теперь условия неравенства принимают вид.
. Теперь условия неравенства принимают вид.

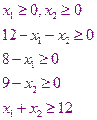
Система этих неравенств определяет область допустимых значений переменных 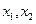 - область
- область 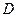 . запишем систему неравенств в виде
. запишем систему неравенств в виде

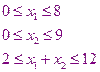

Теперь мы должны найти в этой области точки, обеспечивающие минимум целевой функции. Возьмём 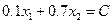 и
и 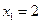
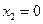 - это точки, которые являются узлами области
- это точки, которые являются узлами области 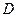 .
.
Минимальное значение целевой функции достигается в вершине области допустимых значений 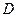 .
.
В общем случае при решении произвольной задачи линейного программирования, область допустимых значений образуется при пересечении конечного числа плоскостей. Эта область может быть как ограниченной, так и неограниченной и даже пустой, если система ограничений противоречива, в последнем случае задача решения не имеет. Обычно область решений представляет собой выпуклый многоугольник. Целевой функции соответствует гиперплоскость. Изменение значения целевой функции соответствует параллельной пересечения гиперплоскости (на единицу меньше). Минимальному значению целевой функции будет соответствовать точка касания гиперплоскости с одной точкой области 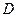 , то есть с одной из вершин многогранника. При минимальном значении целевой функции гиперплоскость может совпадать не с одной точкой, а с одной из граней. В этом случае все точки целевой функции являются решением задачи.
, то есть с одной из вершин многогранника. При минимальном значении целевой функции гиперплоскость может совпадать не с одной точкой, а с одной из граней. В этом случае все точки целевой функции являются решением задачи.
Задача о ресурсах.
В распоряжении бригады имеются следующие ресурсы: 300 кг металла, 100 м2 стекла, 160 чел.-ч. (человеко-часов) рабочего времени. Бригаде поручено изготовлять два наименования изделий: А и Б. Цена одного изделия А 1 тыс. р., для его изготовления необходимо 4 кг металла, 2 м2 стекла и 2 чел.-ч. рабочего времени. Цена одного изделия Б 1.2 тыс. р., для его изготовления необходимо 5 кг металла, 1 м2 стекла и 3 чел.-ч. рабочего времени. Требуется так спланировать объем выпуска продукции, чтобы ее стоимость была максимальной.
Сначала сформулируем задачу математически. Обозначим через 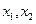 количество изделий А и Б, которое необходимо запланировать (т. е. это искомые величины). Имеющиеся ресурсы сырья и рабочего времени зададим в виде ограничений-неравенств:
количество изделий А и Б, которое необходимо запланировать (т. е. это искомые величины). Имеющиеся ресурсы сырья и рабочего времени зададим в виде ограничений-неравенств:
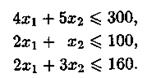
Полная стоимость запланированной к производству продукции выражается формулой
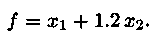
Таким образом, мы имеем задачу линейного программирования, которая состоит в определении оптимальных значений проектных параметров 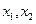 являющихся целыми неотрицательными числами, удовлетворяющих линейным неравенствам и дающих максимальное значение линейной целевой функции.
являющихся целыми неотрицательными числами, удовлетворяющих линейным неравенствам и дающих максимальное значение линейной целевой функции.
Введём дополнительные переменные 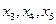 , такие, чтобы при их прибавлении к левым частям соотношений неравенства превращались в равенства. Тогда ограничения примут вид
, такие, чтобы при их прибавлении к левым частям соотношений неравенства превращались в равенства. Тогда ограничения примут вид
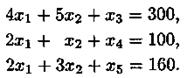
При этом очевидно, что 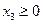 ,
, 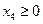 ,
, 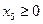 . Заметим, что введение дополнительных неизвестных не повлияло на вид целевой функции, которая зависит только от параметров
. Заметим, что введение дополнительных неизвестных не повлияло на вид целевой функции, которая зависит только от параметров 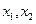 .Фактически
.Фактически 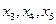 будут указывать остатки ресурсов, не использованные в производстве.
будут указывать остатки ресурсов, не использованные в производстве.
Выразим 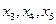 через свободные переменные
через свободные переменные 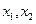 . Получим
. Получим
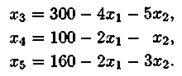
В качестве опорного решения возьмем такое, которое соответствует нулевым значениям свободных параметров:
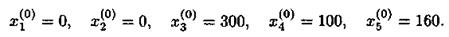
Этому решению соответствует нулевое значение целевой функции
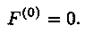
Положим 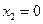 , и будем увеличивать переменную
, и будем увеличивать переменную 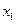 до тех пор, пока переменные
до тех пор, пока переменные 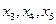 остаются положительными. Отсюда следует, что
остаются положительными. Отсюда следует, что 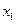 можно увеличить до значения
можно увеличить до значения 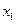 = 50, поскольку при большем его значении переменная х4 станет отрицательной.
= 50, поскольку при большем его значении переменная х4 станет отрицательной.
Таким образом, полагая 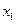 = 50, х2 = 0, получаем новое решение
= 50, х2 = 0, получаем новое решение
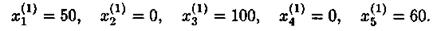
Значение целевой функции при этом будет равно
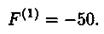
Новое решение лучше, поскольку значение целевой функции уменьшилось по сравнению с предыдущим.
Следующий шаг начнем с выбора нового базиса. Примем ненулевые переменные 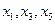 в качестве базисных, а нулевые переменные
в качестве базисных, а нулевые переменные 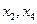 в качестве свободных.
в качестве свободных.
 Получим
Получим

Выражение для целевой функций запишем через свободные параметры. Получим
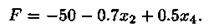
Отсюда следует, что значение целевой функции по сравнению с предыдущей можно уменьшить за счет увеличения х2 поскольку коэффициент при этой переменной в отрицательный. При этом увеличение 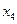 недопустимо, поскольку это привело бы к возрастанию целевой функции; поэтому пусть
недопустимо, поскольку это привело бы к возрастанию целевой функции; поэтому пусть 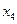 =0.
=0.
Быстрее всех нулевого значения достигнет переменная 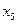 при х2 = 30. Дальнейшее увеличение х2 поэтому невозможно. Следовательно, получаем новое опорное решение, соответствующее значениям х2 = 30,
при х2 = 30. Дальнейшее увеличение х2 поэтому невозможно. Следовательно, получаем новое опорное решение, соответствующее значениям х2 = 30, 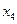 = 0 и тогда
= 0 и тогда
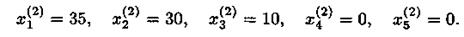
При этом значение целевой функции равно
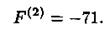
 Покажем, что полученное решение является оптимальным. Для проведения следующего шага ненулевые переменные
Покажем, что полученное решение является оптимальным. Для проведения следующего шага ненулевые переменные 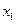 ,
, 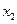 ,
, 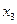 , нужно принять в качестве базисных, а нулевые переменные х4, х5 — в качестве свободных переменных. В этом случае целевую функцию можно записать в виде
, нужно принять в качестве базисных, а нулевые переменные х4, х5 — в качестве свободных переменных. В этом случае целевую функцию можно записать в виде
Поскольку коэффициенты при 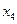 ,
, 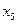 положительные, то при увеличении этих параметров целевая функция возрастает. Следовательно,
положительные, то при увеличении этих параметров целевая функция возрастает. Следовательно, 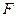 =71 является оптимальным.
=71 является оптимальным.
Таким образом, ответ на поставленную задачу об использовании ресурсов следующий: для получения максимальной суммарной стоимости продукции при заданных ресурсах необходимо запланировать изготовление изделий А в количестве 35 штук и изделий Б в количестве 30 штук. Суммарная стоимость продукции равна 71 тыс. р. При этом все ресурсы стекла и рабочего времени будут использованы, а металла останется 10 кг.
Дата добавления: 2017-03-12; просмотров: 2031;











