В этом случае получаем уравнение

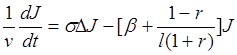(3.11)

Уравнение получено в приближении значений r, близких к единице.

Точность уравнения (3.11) при малых r повысится, если второй член в квадратных скобках заменить на величину

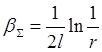. , (3.12)

имеющую смысл потерь на излучение.

В этом случае уравнение (3.11) будет иметь вид:

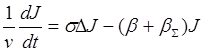(3.11а)

При малых r уравнения тождественны, в чем легко убедиться, вспомнив разложение логарифма в ряд Тейлора:

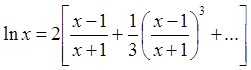
Первый член в правой части уравнения (3.11а) описывает процесс усиления интенсивности света вследствие вынужденного излучения. Второй член характеризует потери, связанные с наличием нерезонансного поглощения и рассеяния в активной среде, а также с выводом выходного излучения через выходное зеркало.

Для начала развития генерации из шумовых (спонтанных) фотонов необходимо, чтобы производная в (3.11а) стала больше 0. Значение инверсной населенности, при котором усиление равно потерям называется пороговым, и оно равно:

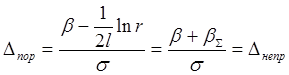(3.13)

Это же условие соответствует работе лазера в непрерывном режиме, когда интенсивность излучения постоянна. Отсюда следует справедливое для любых значений r соотношение

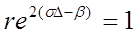(3.14)

Отметим, что если оба зеркала имеют отличные от 1 коэффициенты отражения r₁иr₂, то в выведенных формулах величина r заменяется на произведение r₁r₂.

В лазерной технике часто используются резонаторы, в которых зеркала расположены не на торцах активного элемента, то есть активная среда не полностью заполняет резонатор. Нетрудно показать, что в этом случае надо левую часть уравнения умножить на коэффициент

,

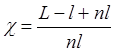где l – длина активного элемента, L – длина резонатора, n – показатель преломления.

Этот коэффициент имеет смысл коэффициента заполнения резонатора, и чем он больше, тем медленнее протекают процессы в лазере.