Метод простых итераций.

Представим нелинейное уравнение: 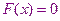в виде 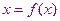.Это преобразование можно сделать различными способами.

Например:

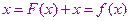
Пусть 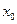является нулевым приближением корня уравнения 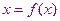, тогда в качестве первого приближения берем 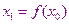, а второе 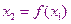. Допустим, мы нашли приближенное значение корня 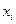на итерационном шаге 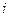, тогда 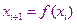(Эта формула отражает алгоритм нахождения корня методом простых итераций)

Проиллюстрируем этот метод графически:

Итерационный процесс сходится

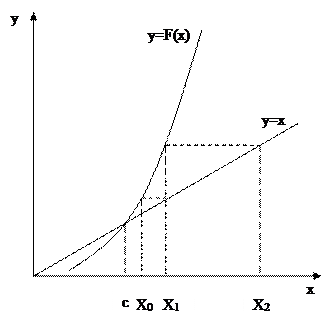
Итерационный процесс расходится

Для сходимости итерационного процесса достаточно, чтобы выполнялось условие 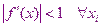; в противном случае итерационный процесс может расходиться.

Сходимость метода может зависеть от удачного преобразования 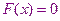к .

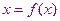Например:

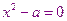- это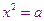

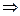
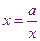
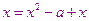
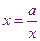
Метод 12

Метод Хорд

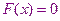Предположим, что мы нашли 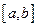, на концах которого 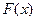меняет знак

и что в точке 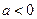, а в точке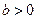

В методе хорд, как и в методе половинного деления на каждом итерационном шаге происходит последовательное сужение отрезка 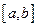, содержащего корень. В методе хорд на каждом итерационном шаге в качестве одного из концов такого суженного отрезка берется точка пересечения хорды AB с осью OX.

Получим соотношение для определения точки С.

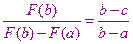
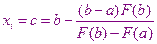
Получил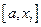и и 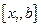теперь ищем, где есть разность знаков, а дальше как в методе половинного деления.

Итерационный процесс повторяем до тех пор, пока не будет достигнута заданная точность 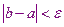. Также как и метод половинного деления гарантировано сходится, однако в ряде случаев он имеет более быструю сходимость.

Метод 13