Метод Ньютона (касательных).

Метод Ньютона сходим с методом хорд. Его отличие от метода хорд состоит в том, что на каждом итерационном шаге вместо хорды проводится касательная к кривой 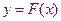и ищется точка пересечения касательной с осью абсцисс, которая и определяет следующее приближение корня.

Не нужно искать 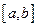, сначала задается .

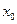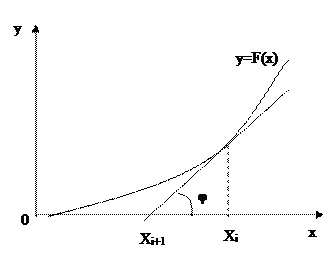
Получим формулу для определения корня на 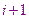итерационном шаге.

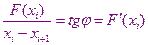
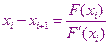
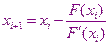
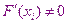
На каждом итерационном шаге объём вычислений в методе Ньютона несколько больший, чем в ранее рассмотренных методах, потому что приходится находить значения не только функции 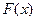, но и её производной. Однако скорость сходимости этого метода в ряде случаев значительно выше, чем в других методах. Поэтому метод Ньютона является одним из самых распространенных методов решения нелинейных уравнений.

Сходимость метода Ньютона в значительной степени зависит от выбора начального приближения 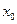, чем ближе 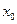к корню, тем сходимость лучше, поэтому иногда целесообразно использовать смешанный алгоритм. Нужно учитывать возможность расхождения.

Во всех итерационных процессах ошибка округления не накапливается. Это является одним из самых важнейших преимуществ этих методов.

Определенными особенностями обладает нахождение корней алгебраических выражений. Предположим, 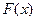есть полином степени 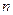, этот полином имеет 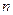корней. Корни алгебраических уравнений можно в ряде случаев находить последовательно. Предположим сначала каким-то методом (методом половинного деления) нашли корень 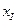, после этого получаем

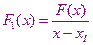и строим эту функцию 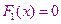, решаем и находим 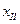получаем

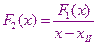и решаем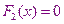

Тема №4