Решение систем линейных уравнений.
Системы линейных алгебраических уравнений (СЛАУ) в научно-исследовательской инженерной практике встречаются весьма часто. К решению систем линейных уравнений сводится многочисленные практические задачи с использованием численных методов.
Например:
Коэффициенты сплайнов находятся путем решения СЛАУ. К СЛАУ приводят уравнения частных производных.
Задачи по нахождению собственных значений также приводят к СЛАУ. Таким образом, решение СЛАУ – одна из самых распространенных и важных задач вычислительной математики.
Запишем СЛАУ в общем виде:
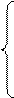
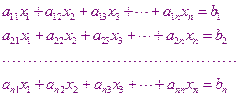
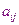
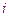 - номер уравнения
- номер уравнения
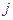 - номер неизвестной, на которую умножается коэффициент.
- номер неизвестной, на которую умножается коэффициент.
Коэффициенты образуют матрицу
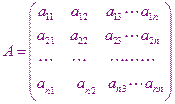
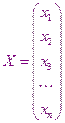
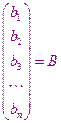
Матрица системы столбец неизвестных величин столбец правых частей
Введя эти величины, мы можем записать СЛАУ в виде матричного решения
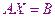
Важнейшей характеристикой квадратной матрицы является её определитель( 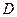 )
)
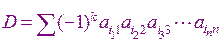
Число возможных значений 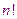
В курсе высшей математики показывается, что система СЛАУ имеет единственное решение, если определитель системы не равен нулю. В этом случае решение может быть найдено с помощью формул Крамера:
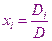 ,
,
где 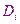 - определитель матрицы, которая получается после исключения в матрице А
- определитель матрицы, которая получается после исключения в матрице А 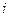 -го столбца и его замены столбцом свободных членов.
-го столбца и его замены столбцом свободных членов.
Если определитель системы равен нулю, то в этом случае матрица 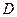 называется вырожденной, а система либо не имеет решения, либо имеет бесконечное множество решений. Для некоторых систем решение оказывается очень чувствительным к малым погрешностям в исходных данных
называется вырожденной, а система либо не имеет решения, либо имеет бесконечное множество решений. Для некоторых систем решение оказывается очень чувствительным к малым погрешностям в исходных данных 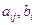 . Такие системы называются плохо-обусловленными. Определитель плохо-обусловленных систем близок к нулю. При численных вычислениях всегда надо иметь ввиду эту особенность систем линейных уравнений.
. Такие системы называются плохо-обусловленными. Определитель плохо-обусловленных систем близок к нулю. При численных вычислениях всегда надо иметь ввиду эту особенность систем линейных уравнений.
Существуют методы улучшения обусловленности систем. Некоторые некорректные задачи приводят к плохо обусловленным системам уравнений. Эти задачи могут иметь важное практическое значение. Существуют методы решения таких задач.
Методы решения СЛАУ делятся на 2 группы:
1)прямые
используют готовые формулы для вычисления неизвестных, эти методы наиболее универсальны, пригодны для решения широкого класса СЛАУ. Но они обладают недостатками: они требуют хранения в оперативной памяти сразу всей матрицы. Существенным недостатком прямых методов является накапливание погрешности в процессе решения. Это особенно опасно для больших систем, а также для плохо-обусловленных , поэтому прямые методы используют обычно если 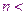 нескольких сотен.
нескольких сотен.
Итерационные
в итерационных методах решение находят путем последовательных приближений. Накапливание погрешности не происходит, и с помощью них решают систему с большим числом уравнений и для решения плохо-обусловленных систем. Однако сходимость итерации может быть очень медленной. Поэтому время счета может быть очень большим. Другим недостатком является то, что с их помощью решается ограниченный класс уравнений.
Например:
Уравнений с преобладанием диагональных элементов, либо системы со слабо заполненными матрицами.
Метод Крамера относится к прямому методу, однако на практике метод Крамера практически никогда не используется, так как он требует большого объёма вычислений. Оценим объём вычислений с помощью метода Крамера. Для применения этого необходимо вычислить 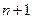 определитель, а для вычисления каждого определителя необходимо сделать
определитель, а для вычисления каждого определителя необходимо сделать 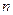 произведений, а число полученных слагаемых
произведений, а число полученных слагаемых 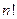 . Значит, число арифметических операций будет
. Значит, число арифметических операций будет 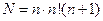 с ростом
с ростом 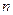 резко возрастает при
резко возрастает при 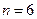
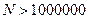
Наиболее распространенным среди прямых методов является метод Гаусса.
Метод 14
Метод Гаусса.
Метод Гаусса основан на приведении матрицы системы к треугольному виду. Метод Гаусса состоит из двух этапов: прямой ход и обратный. Прямой ход – матрица приводится к треугольному виду, при обратном последовательно находятся неизвестные величины.
Прямой ход состоит в следующем:
1)на первом шаге с помощью первого уравнения исключается 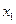 из всех последних уравнений системы, в результате получается новая система, имеющая то же решение, но в первом столбце матрицы будет не нулевым только первый элемент.
из всех последних уравнений системы, в результате получается новая система, имеющая то же решение, но в первом столбце матрицы будет не нулевым только первый элемент.
2)на втором шаге с помощью второго уравнения исключается 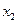 из всех уравнений. Этот процесс продолжается до тех пор, пока в левой части последнего
из всех уравнений. Этот процесс продолжается до тех пор, пока в левой части последнего 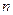 - го уравнения не останется лишь один член с неизвестным
- го уравнения не останется лишь один член с неизвестным 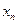 .
.
Рассмотрим процесс исключения подробнее:
На 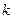 -ом шаге исключается
-ом шаге исключается 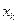
Запишем 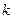 -ое уравнение:
-ое уравнение:
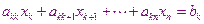
Исключим с помощью этого уравнения 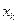 из уравнения с номером
из уравнения с номером 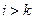
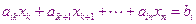
Для исключения из 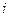 -го уравнения вычитаем
-го уравнения вычитаем 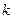 -ое , умноженное на
-ое , умноженное на 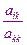 .
.
После такого вычитания первые слагаемые сокращаются. Запишем значение коэффициенты перед 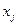 , используем для него прежнее обозначение
, используем для него прежнее обозначение
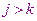
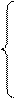
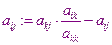
При этом изменяется свободный член
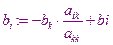
По завершению прямого хода получается система с треугольной матрицей. Далее производится обратный ход метода Гаусса.
Обратный ход метода Гаусса состоит в последовательном вычислении искомых неизвестных, начиная с 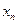 . Сначала находится
. Сначала находится 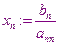 . Далее, используя это значение, находится
. Далее, используя это значение, находится 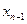 и так далее.
и так далее.
Например:
На 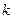 - ом шаге обратного хода неизвестные находятся с помощью выражения.
- ом шаге обратного хода неизвестные находятся с помощью выражения.
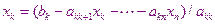
В процессе исключения неизвестных приходится делить на диагональный элемент, который может оказаться равным нулю. Чтобы исключить эту ситуацию, необходимо на каждом шаге прямого хода менять расположение уравнений таким образом, чтобы диагональный элемент 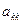 не был равным нулю, а лучше, чтобы он имел максимально возможное значение.
не был равным нулю, а лучше, чтобы он имел максимально возможное значение.
Перестановка уравнений должна быть предусмотрена в вычислительном алгоритме и метод Гаусса, в котором производится перестановка уравнений таким образом, чтобы диагональный элемент имел максимальное значение, называется метод Гаусса с выбором главного элемента.
В методе Гаусса объём вычислений пропорционален 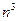 . Существует практически значимые случаи, когда объём вычислений при решении СЛАУ можно резко сократить.
. Существует практически значимые случаи, когда объём вычислений при решении СЛАУ можно резко сократить.
Метод 15
Метод прогонки.
Метод прогонки является модификацией метода Гаусса для частного случая с трёхдиагональной матрицей. Такие системы возникают при численном решении уравнений математической физики.
Другой пример: коэффициенты сплайна третьей степени находятся путём решения систем с трёхдиагональной матрицей.
В методе прогонки объём вычислений растет пропорционально 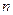 . Запишем систему уравнений, которая решается методом прогонки.
. Запишем систему уравнений, которая решается методом прогонки.
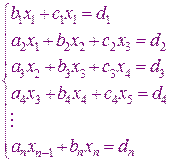
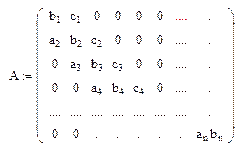
Общий вид уравнений с трёхдиагональной матрицей
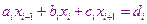
Решение системы с трёхдиагональной матрицей, как и в методе Гаусса, состоит из двух этапов. Прямой прогонки и обратной прогонки.
Рассмотрим первый этап (прямой ход метода прогонки)
Для этого неизвестный 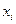 выражаем через
выражаем через 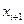 , таким образом:
, таким образом:
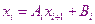 ,
,
где 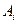 ,
, 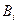 - неизвестные пока (прогоночные) коэффициенты. На первом как раз и находится эти коэффициенты. Сравним это уравнение при
- неизвестные пока (прогоночные) коэффициенты. На первом как раз и находится эти коэффициенты. Сравним это уравнение при 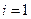 с первым уравнением системы
с первым уравнением системы
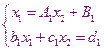
И из сравнения находим, что
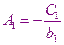
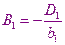
Заменим i-ое уравнение системы, выразив в нём 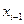 с помощью
с помощью 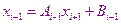
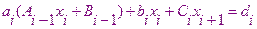
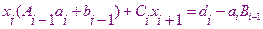
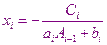
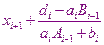
Сравнивая с
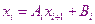
Получаем рекуррентные соотношения для нахождения прогоночных коэффициентов.
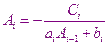
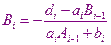
После того как найдены все прогоночные коэффициенты в результате прямого хода метода, находят 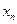 . Для этого сравниваем последние уравнения системы с последним прогоночным соотношением. В результате получаем систему из двух уравнений с двумя неизвестными.
. Для этого сравниваем последние уравнения системы с последним прогоночным соотношением. В результате получаем систему из двух уравнений с двумя неизвестными.
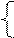
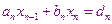
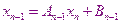
Отсюда
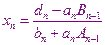
Это фактически начало обратного хода метода прогонки.
После этого последовательно находим 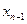 …….и т.д. вплоть до
…….и т.д. вплоть до 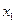 .
.
Метод 16
Дата добавления: 2017-03-12; просмотров: 2934;











