II.2.2 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ЗАДАЧА № II.21Поезд подходит к станции и замедляет свое движение. В каком направлении в это время легче тащить тяжелый ящик по полу вагона: по ходу поезда или в обратную сторону?
Ответ. По ходу поезда.
ЗАДАЧА № II.22Что произошло бы с людьми, если бы Земля внезапно остановилась и прекратила свое движение вокруг Солнца?
Ответ. Люди по инерции с огромной скоростью полетели бы от Земли.
ЗАДАЧА № II.23В зоопарках белок помещают в цилиндрический барабан, где имеются спицы. Барабан подвешен на оси, вокруг которой он может свободно вращаться. В какую сторону и почему барабан вращается во время движения белки по спицам?
Ответ. Барабан вращается в сторону, противоположную движению белки, которая при своем беге отталкивается от спиц, приводя барабан в движение.
ЗАДАЧА № II.24Предложите способ определения вместимости сосуда, в котором находится вода, используя только весы и разновес.
Ответ. Сначала с помощью весов определяют массу стакана, а затем, заполнив его полностью водой, снова ставят на весы. По плотности и массе воды, находящейся в стакане, определяют вместимость этого стакана.
ЗАДАЧА № II.25Почему в конце прыжка спортсмен опускается на согнутые ноги?
Ответ. Сгибая ноги в конце прыжка, спортсмен как бы увеличивает тормозной путь, а следовательно, уменьшает силу удара о поверхность Земли.
ЗАДАЧА № II.26В кинофильмах каскадер часто совершает в прыжке пересадку с одного автомобиля на другой. Почему это опасно делать при большой разнице в скоростях автомобилей?
Ответ. При пересадке каскадер испытывает большое изменение скорости за короткий промежуток времени. В результате он переносит большие перегрузки, что для человека опасно.
ЗАДАЧА № II.27Океанский лайнер при столкновении с маленьким пароходом может потопить его почти без всяких для себя повреждений. Как это согласуется с третьим законом Ньютона?
Ответ. Массы лайнера и парохода разные. В результате столкновения суда приобретают разные ускорения, что приводит к их различным повреждениям.
ЗАДАЧА № II.28На внутренней стенке закрытой банки, уравновешенной на чувствительных весах, сидит муха. Что произойдет с весами, если муха станет летать внутри банки?
Ответ. Покинув стенку банки и держась в воздухе на одном уровне, муха давит крылышками на воздух силой, равной собственному весу. Это давление передается дну банки. Следовательно, весы останутся в равновесии. Если же, летая в банке, муха поднимается вверх или опускается вниз, то чувствительные весы должны покачнуться.
ЗАДАЧА № II.29Мальчик везет санки. Сила, с которой он их тянет, равна силе, с которой санки противодействуют этому движению. Казалось бы, санки должны оставаться на месте. Почему же они движутся?
Ответ. Сила, с которой мальчик тянет санки, вполне достаточна для того, чтобы они двигались. Однако такая же по модулю сила, противодействующая этому движению, недостаточна, чтобы преодолеть значительное сцепление подошв его обуви с поверхностью снега или льда.
ЗАДАЧА № II.30Почему трудно разбить орех на мягкой опоре и легко его разбить на твердой опоре?
Ответ. Чтобы разбить орех, надо приложить к нему две равные, но противоположно направленные силы, которые сожмут его так, что скорлупа разрушится. Одна сила характеризует взаимодействие ореха с молотком, а другая — взаимодействие ореха с опорой. Если опора твердая и неподвижная, то эти условия соблюдаются. Если опора мягкая, то при ударе орех приобретает скорость, но, углубляясь в мягкую опору, он эту скорость теряет, поэтому скорлупа почти не изменяет своей формы и орех не разрушается.
ЗАДАЧА № II.31Вагон массой 20 т движется равнозамедленно с ускорением 0,3 м/с2 и начальной скоростью 54 км/ч. Найти силу торможения, действующую на вагон, время движения вагона до остановки и перемещение вагона.
Дано: 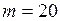 т =
т = 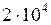 кг;
кг;
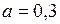 м/с2;
м/с2;
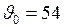 км/ч =
км/ч = 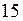 м/с.
м/с.
Найти: 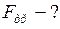
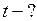
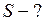
Решение

На вагон, движущийся вдоль оси  действуют: сила тяжести (
действуют: сила тяжести ( 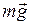 ); сила трения (
); сила трения ( 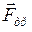 ); сила нормальной реакции опоры (
); сила нормальной реакции опоры ( 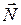 ) (рис.55).
) (рис.55).
Запишем второй закон Ньютона в векторной форме:
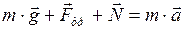 . (1)
. (1)
Направление вектора скорости совпадает с направлением оси  . Вектор ускорения будет направлен в сторону противоположную направлению движения (так как движение вагона равнозамедленное).
. Вектор ускорения будет направлен в сторону противоположную направлению движения (так как движение вагона равнозамедленное).
Проецируем обе части уравнения (1) на ось  :
:
 :
: 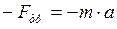 или
или 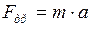 ;
; 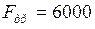 Н = 6 кН.
Н = 6 кН.
Время движения вагона до остановки найдём из уравнения (II.8): 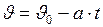 , так как
, так как 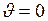 (по условию задачи), то:
(по условию задачи), то:
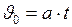 ,
, 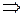
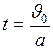 ;
; 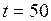 с.
с.
Расстояние, пройденное вагоном до остановки определяется формулой (II.7): 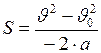 или
или 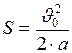 ;
; 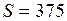 м.
м.
ЗАДАЧА № II.32Тело массой 45 кг перемещается по горизонтальной плоскости под действием силы 294 Н, направленной под углом 300 к горизонту. Коэффициент трения груза о плоскость 0,1. Определить ускорение движения груза.
Дано: 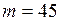 кг;
кг;
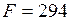 Н;
Н;
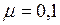 ;
;
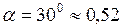 рад
рад
Найти: 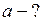
Решение

На тело действуют: сила тяжести ( 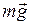 ); сила трения (
); сила трения ( 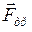 ); сила нормальной реакции опоры (
); сила нормальной реакции опоры ( 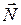 ); сила тяги (
); сила тяги ( 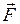 ) (рис.56).
) (рис.56).
Направление вектора ускорения (  ) совпадает с направлением оси
) совпадает с направлением оси  .
.
Запишем второй закон Ньютона в векторной форме:
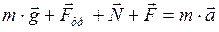 . (1)
. (1)
Проецируем обе части уравнения (1) на оси  и
и 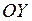 :
:
 :
: 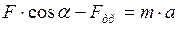 ;
;
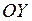 :
: 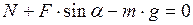 ; (2)
; (2)
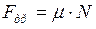
Решим полученную систему уравнений (2) относительно неизвестного параметра (ускорения), получим:
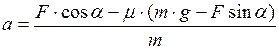 ;
; 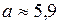 м/с2.
м/с2.
ЗАДАЧА № II.33Тело равномерно скользит по наклонной плоскости с углом наклона 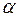 . Определить коэффициент трения тела о плоскость.
. Определить коэффициент трения тела о плоскость.
Дано: 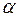
Найти: 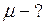
Решение

При скольжении тела по наклонной плоскости на него действуют: сила тяжести ( 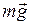 ); сила трения (
); сила трения ( 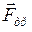 ); сила нормальной реакции опоры (
); сила нормальной реакции опоры ( 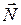 ) (рис.57). Ускорение при равномерном скольжении тела равно нулю.
) (рис.57). Ускорение при равномерном скольжении тела равно нулю.
Запишем второй закон Ньютона в векторной форме:
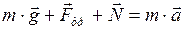 . (1)
. (1)
Проецируем обе части уравнения (1) на оси  и
и 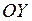 :
:
 :
: 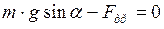 ;
;
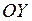 :
: 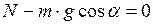 ; (2)
; (2)
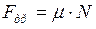
Решим полученную систему уравнений (2) относительно неизвестного параметра (коэффициента трения тела о плоскость), получим:
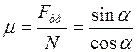 ;
;
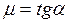 . (3)
. (3)
Уравнение (3) показывает, что если тело равномерно скользит по наклонной плоскости, то коэффициент трения тела о плоскость будет определяться тангенсом угла наклона этой плоскости.
В случае равнопеременного движения данное утверждение не применимо.
ЗАДАЧА № II.34Брусок массой 2 кг скользит по горизонтальной поверхности под действием груза массой 0,5 кг, прикреплённого к концу нерастяжимой нити, перекинутой через неподвижный блок. Коэффициент трения бруска о поверхность 0,1. Найти ускорение движения тела и силу натяжения нити. Массами блока и нити, а также трением в блоке пренебречь.
Дано: 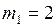 кг;
кг;
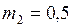 кг;
кг;
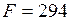 Н;
Н;
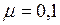 .
.
Найти: 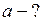
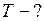
Решение
Будем рассматривать движение каждого тела в отдельности.
Первое тело. На брусок действуют: сила тяжести ( 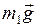 ); сила трения (
); сила трения ( 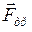 ); сила нормальной реакции опоры (
); сила нормальной реакции опоры ( 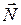 ); сила натяжения нити (
); сила натяжения нити ( 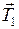 ) (рис.58).
) (рис.58).

Запишем для бруска второй закон Ньютона в векторной форме:
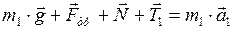 . (1)
. (1)
Проецируем обе части уравнения (1) на оси  и
и 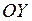 :
:
 :
: 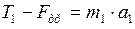
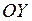 :
: 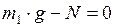 (2)
(2)
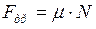
После ряда преобразований системы уравнений (2), получим:
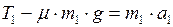 . (3)
. (3)
Второе тело. На груз действуют: сила тяжести ( 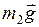 ); сила натяжения нити (
); сила натяжения нити ( 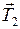 ) (рис.58).
) (рис.58).
Запишем для груза второй закон Ньютона в векторной форме:
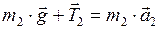 . (4)
. (4)
Проецируем обе части уравнения (4) на ось 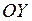 :
:
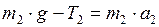 . (5)
. (5)
Складывая уравнения (3) и (5) и учитывая, что 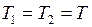 , а
, а 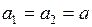 , получаем:
, получаем: 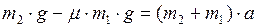 . Выразим из последнего равенства ускорение:
. Выразим из последнего равенства ускорение:
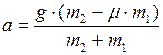 ;
; 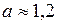 м/с2.
м/с2.
Силу натяжения нити находим из уравнения (5):
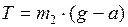 ;
; 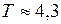 Н.
Н.
ЗАДАЧА № II.35Груз массой 5 кг, связанный нерастяжимой нитью, перекинутой через неподвижный блок, с другим грузом массой 2 кг, движется вниз по наклонной плоскости. Найти силу натяжения нити и ускорение грузов, если коэффициент трения между первым грузом и плоскостью 0,1. Угол наклона плоскости к горизонту 360. Массами нитей и блока, а также трением в блоке пренебречь.
Дано: 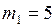 кг;
кг;
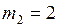 кг;
кг;
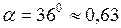 рад;
рад;
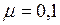 .
.
Найти: 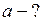
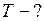
Решение

Рассмотрим движение каждого груза в отдельности.
Первый груз. На груз действуют: сила тяжести ( 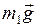 ); сила трения (
); сила трения ( 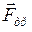 ); сила нормальной реакции опоры (
); сила нормальной реакции опоры ( 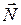 ); сила натяжения нити (
); сила натяжения нити ( 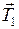 ) (рис.59).
) (рис.59).
Запишем для груза второй закон Ньютона в векторной форме:
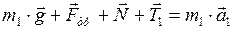 . (1)
. (1)
Проецируем обе части уравнения (1) на оси  и
и 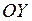 :
:
 :
: 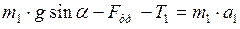 ;
;
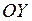 :
: 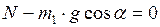 ; (2)
; (2)
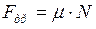
Преобразуем систему уравнений (2) к виду:
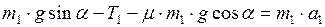 . (3)
. (3)
Второй груз. На груз действуют: сила тяжести ( 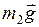 ); сила натяжения нити (
); сила натяжения нити ( 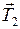 ) (рис.59).
) (рис.59).
Запишем для груза второй закон Ньютона в векторной форме:
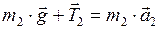 . (4)
. (4)
Проецируем обе части уравнения (4) на ось 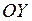 :
:
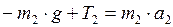 . (5)
. (5)
Складывая уравнения (3) и (5) и учитывая, что 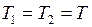 , а
, а 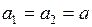 , получаем:
, получаем: 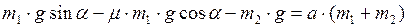 . Выразим из последнего равенства ускорение:
. Выразим из последнего равенства ускорение:
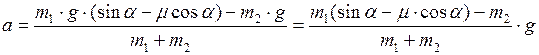 ;
;
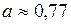 м/с2.
м/с2.
Силу натяжения нити находим из уравнения (5):
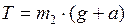 ;
; 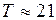 Н.
Н.
ЗАДАЧА № II.36Невесомый блок укреплён на вершине двух наклонных плоскостей, составляющих с горизонтом углы 300 и 450. Гири 1 и 2 массой 1 кг каждая соединены нитью, перекинутой через блок. Найти ускорение, с которым движутся гири, и силу натяжения нити. Считать нить невесомой и нерастяжимой. Трением пренебречь.
Дано: 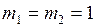 кг;
кг;
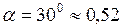 рад;
рад;
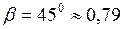 рад.
рад.
Найти: 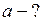
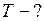
Решение
Рассмотрим движение каждой гири в отдельности.
Первая гиря. На гирю действуют: сила тяжести ( 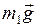 ); сила нормальной реакции опоры (
); сила нормальной реакции опоры ( 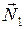 ); сила натяжения нити (
); сила натяжения нити ( 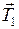 ) (рис.60).
) (рис.60).
Запишем для гири второй закон Ньютона в векторной форме:
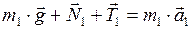 . (1)
. (1)
Проецируем обе части уравнения (1) на оси 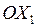 и
и 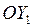 :
:
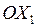 :
: 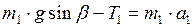 ; (2)
; (2)
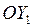 :
: 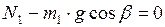 . (3)
. (3)

Вторая гиря. На гирю действуют: сила тяжести ( 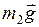 ); сила нормальной реакции опоры (
); сила нормальной реакции опоры ( 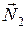 ); сила натяжения нити (
); сила натяжения нити ( 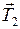 ) (рис.60).
) (рис.60).
Запишем для гири второй закон Ньютона в векторной форме:
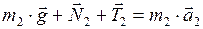 . (4)
. (4)
Проецируем обе части уравнения (3) на оси 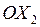 и
и 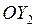 :
:
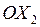 :
: 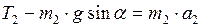 ; (5)
; (5)
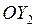 :
: 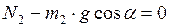 ; (6)
; (6)
Уравнения (3) и (6) в данной задаче не используются, так как силой трения пренебрегаем.
Складывая уравнения (2) и (5) и учитывая, что 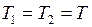 , а
, а 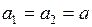 , получаем:
, получаем: 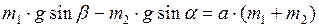 . Выразим из последнего равенства ускорение:
. Выразим из последнего равенства ускорение:
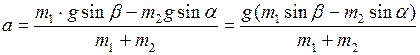 ;
; 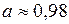 м/с2.
м/с2.
Силу натяжения нити найдём из (2):
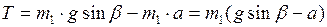 ;
; 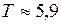 Н.
Н.
ЗАДАЧА № II.37Три тела массами  ,
, 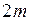 и
и 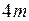 связаны нитями и находятся на гладком горизонтальном столе. К телу массой
связаны нитями и находятся на гладком горизонтальном столе. К телу массой  приложена горизонтальная сила
приложена горизонтальная сила 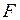 (рис.61). Определить силу натяжения между грузами
(рис.61). Определить силу натяжения между грузами 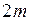 и
и 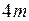 .
.
Дано:  ;
; 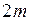 ;
; 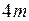 ;
; 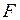 .
.
Найти: 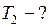
Решение

Так как поверхность стола гладкая, влиянием силы трения можно пренебречь.
Запишем второй закон Ньютона для каждого из тел:
Первое тело. На тело действуют: сила тяжести ( 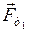 ); сила нормальной реакции опоры (
); сила нормальной реакции опоры ( 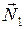 ); сила натяжения нити (
); сила натяжения нити ( 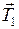 ); сила тяги (
); сила тяги ( 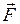 ) (рис.61).
) (рис.61).
Запишем для этого тела второй закон Ньютона в векторной форме:
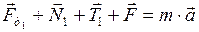 . (1)
. (1)
Проецируем обе части уравнения (1) на ось  :
:
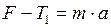 (2)
(2)
Второе тело. На тело действуют: сила тяжести ( 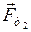 ); сила нормальной реакции опоры (
); сила нормальной реакции опоры ( 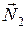 ); сила натяжения нити (
); сила натяжения нити ( 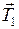 ); сила натяжения нити (
); сила натяжения нити ( 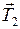 ) (рис.61).
) (рис.61).
Запишем для этого тела второй закон Ньютона в векторной форме:
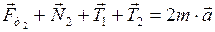 . (3)
. (3)
Проецируем обе части уравнения (3) на ось  :
:
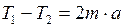 (4)
(4)
Третье тело. На тело действуют: сила тяжести ( 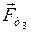 ); сила нормальной реакции опоры (
); сила нормальной реакции опоры ( 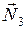 ); сила натяжения нити (
); сила натяжения нити ( 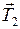 ) (рис.61).
) (рис.61).
Запишем для этого тела второй закон Ньютона в векторной форме:
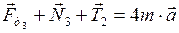 . (5)
. (5)
Проецируем обе части уравнения (5) на ось  :
:
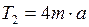 . (6)
. (6)
Проекция на ось 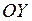 в данной задаче не используется.
в данной задаче не используется.
Сложив почленно, левые и правые части уравнений: (2), (4) и (6), получим:
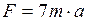 . (7)
. (7)
Выразим из уравнения (7), ускорение движения тел: 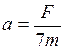 и подставим его в формулу (6), получим:
и подставим его в формулу (6), получим:
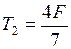 .
.
ЗАДАЧА № II.38На доске 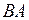 (рис.62), равномерно вращающейся вокруг вертикальной оси
(рис.62), равномерно вращающейся вокруг вертикальной оси 
 , укреплён на вертикальной стойке, отстоящей от оси вращения на расстоянии 5 см, отвес. Какова частота вращения доски, если нить отвеса длиной 8 см отклонилась от вертикали на угол 400?
, укреплён на вертикальной стойке, отстоящей от оси вращения на расстоянии 5 см, отвес. Какова частота вращения доски, если нить отвеса длиной 8 см отклонилась от вертикали на угол 400?
Дано: 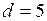 см =
см = 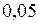 м;
м;
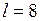 см =
см = 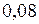 м;
м;
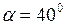 .
.
Найти: 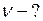
Решение

Запишем второй закон Ньютона:
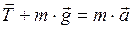 (1)
(1)
Проецируем обе части уравнения (2) на оси  и
и 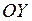 :
:
 :
: 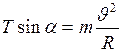 ; (2)
; (2)
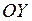 :
: 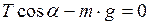 . (3)
. (3)
Перепишем уравнение (3) в виде:
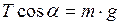 . (4)
. (4)
Поделим почленно уравнение (2) на уравнение (4), получим:
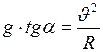 . (5)
. (5)
Линейная скорость точки связана с угловой скоростью соотношением (II.25):
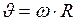 , (6)
, (6)
где
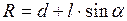 , (7)
, (7)
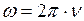 . (8)
. (8)
Выразим из уравнения (8) частоту 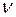 и введём соответствующие замены, получим:
и введём соответствующие замены, получим:
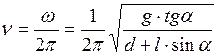 ;
; 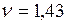 с-1.
с-1.
ЗАДАЧА № II.39 Ведёрко с водой вращают в вертикальной плоскости на верёвке длиной 0,5 м. С какой наименьшей скоростью нужно его вращать, чтобы при прохождении через верхнюю точку удержать воду в ведёрке?
Дано: 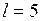 см =
см = 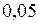 м;
м;
Найти: 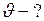
Решение
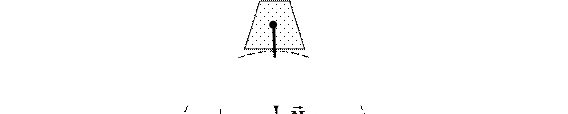
На воду в верхней точке траектории действуют: сила тяжести ( 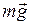 ); сила нормальной реакции дна (
); сила нормальной реакции дна ( 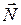 ) (рис.63).
) (рис.63).
Запишем второй закон Ньютона в векторной форме:
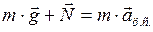 , (1)
, (1)
где 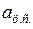 - центростремительное ускорение, оно равно:
- центростремительное ускорение, оно равно:
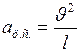 . (2)
. (2)
Направим ось 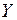 вертикально вниз к центру окружности
вертикально вниз к центру окружности 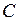 . Проецируем обе части уравнения (1) на ось
. Проецируем обе части уравнения (1) на ось 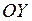 и с учётом (2):
и с учётом (2):
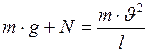 . (3)
. (3)
В момент отрыва воды от дна ведёрка 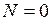 , поэтому
, поэтому
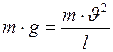 . (4)
. (4)
Выразим из уравнения (4) наименьшую скорость вращения ведёрка:
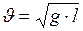 ;
; 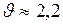 м/с.
м/с.
ЗАДАЧА № II.40Жёсткость одной пружины равна 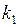 , а другой
, а другой 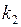 . Какова жёсткость
. Какова жёсткость 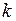 пружины, составленной из этих пружин соединённых: а) последовательно; б) параллельно.
пружины, составленной из этих пружин соединённых: а) последовательно; б) параллельно.
Дано: 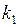 ;
; 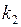 .
.
Найти: 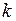 -?
-?
Решение
а) При последовательном соединении пружин:
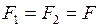 , (1)
, (1)
где
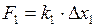 ;
; 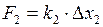 ;
; 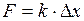 . (2)
. (2)
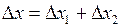 . (3)
. (3)
Выразим из формулы (2) следующие величины: 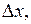
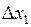 ,
, 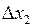 и подставим их в формулу (3), а также учитывая равенство (1), получим:
и подставим их в формулу (3), а также учитывая равенство (1), получим:
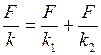 . (4)
. (4)
Перепишем уравнение (4) в виде:
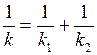 . (5)
. (5)
Выразим из последней формулы жёсткость пружины 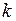 , получим:
, получим:
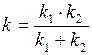 .
.
б) При параллельном соединении пружин: 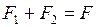 , а
, а 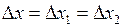 . Учитывая, что
. Учитывая, что 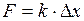 , получим
, получим
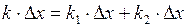 или
или 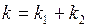 .
.
Дата добавления: 2016-09-06; просмотров: 5757;











