II.6.2 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ЗАДАЧА № II.98Алюминиевый и железный шары одинаковой массы уравновешены на рычаге. Нарушится ли равновесие, если шары погрузить в воду?
Ответ. Плотность железа больше, чем алюминия, следовательно, при равной массе объём алюминиевого шара больше (рис.79), что приведёт к возникновению для него большей силы Архимеда. Плечи сил, приложенных к шарам, равны. Значит, железный шар окажется в воде ниже.

ЗАДАЧА № II.99Алюминиевый и железный шары одинаковой массы уравновешены на рычаге. Нарушится ли равновесие, если шары погрузить в воду? Влиянием выталкивающей силы со стороны воздуха пренебречь.
Ответ. При равном объёме шаров масса железного шара будет больше. Чтобы шары оказались уравновешены, плечо силы, действующей на железный шар, должно быть меньше (рис.80). В воде возникают равные силы Архимеда 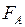 . Но момент силы
. Но момент силы 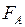 для железного шара будет меньше, чем для алюминиевого. Значит, рычаг будет вращаться против часовой стрелки, и железный шар опустится.
для железного шара будет меньше, чем для алюминиевого. Значит, рычаг будет вращаться против часовой стрелки, и железный шар опустится.

ЗАДАЧА № II.100Справедливы лив условиях невесомости законы Паскаля и Архимеда?
Ответ. Сила Архимеда равна весу вытесненной телом жидкости, а при невесомости вес равен нулю. Равенство давления по всем направлениям определяется одинаковой вероятностью теплового движения по всем направлениям. Следовательно, закон Паскаля справедлив, а закон Архимеда– нет.
ЗАДАЧА № II.101Сообщающиеся сосуды А и В наполнены водой. В сосуд А опускают деревянный кубик. Как изменится уровень воды в сосудах?
Ответ. Поскольку кубик вытеснит часть воды, то уровни воды повысятся в обоих сосудах, но в сосуде Аон будет выше, так как плотность кубика меньше, чем воды, и избыточный столбик воды скомпенсирует уменьшение давления в сосуде А.
ЗАДАЧА № II.102В стакане с водой плавал кусок льда. Лёд растаял. Как изменится уровень воды в стакане?
Ответ. Плавающий лёд занимает в воде объём 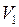 . Этот объём может быть найден из условия плавания тел:
. Этот объём может быть найден из условия плавания тел: 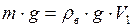 , где
, где  - масса льда, а
- масса льда, а 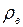 - плотность воды. Отсюда
- плотность воды. Отсюда 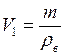 . После таяния масса получившейся воды равна массе льда, и объём воды
. После таяния масса получившейся воды равна массе льда, и объём воды 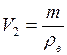 , т.е.
, т.е. 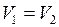 . Это значит, что образовавшаяся вода заполнит объём выемки, оставшейся в стакане после таяния льда.
. Это значит, что образовавшаяся вода заполнит объём выемки, оставшейся в стакане после таяния льда.
ЗАДАЧА № II.103Однаиз бутылок наполнена водой, другая – ртутью. Потонет ли бутылка с водой, если её опустить в воду? Потонет ли бутылка с ртутью, если её опустить в ртуть?
Ответ. Условие плавания: вес тела равен выталкивающей силе. Если вес больше выталкивающей силы, тело тонет. Бутылка с водой потонет в воде, так как вес стекла больше действующей на него выталкивающей силы ( 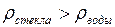 ). Бутылка со ртутью не потонет в ртути, так как вес стекла меньше действующей на него выталкивающей силы (
). Бутылка со ртутью не потонет в ртути, так как вес стекла меньше действующей на него выталкивающей силы ( 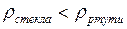 ).
).
ЗАДАЧА № II.104НаЗемле тело, плотность которого вдвое больше плотности воды, погрузили в сосуд с водой. Что произойдёт с этим телом на Луне?
Ответ. Условие равновесия плавающего тела не зависит от ускорения свободного падения. Описанное тело на Земле тонет, поэтому оно будет лежать на дне сосуда и на Луне.
ЗАДАЧА № II.105Одинаковая ли выталкивающая сила действует на тело, если его погружать в жидкость на разную глубину?
Ответ. Одинаковая, так как выталкивающая сила зависит только от плотности жидкости и не зависит от глубины погружения тела.
ЗАДАЧА № II.106В пресной или морской воде осадка судна больше?
Ответ. Осадка судна в морской воде меньше, чем в пресной, так как плотность морской воды больше, чем пресной.
ЗАДАЧА № II.107В цилиндрическом сосуде с водой плавает кусок льда. Как изменится уровень воды в сосуде, когда лёд растает? Изменится ли уровень воды, если внутри льда будет находиться кусок свинца?
Ответ. Так как вес всего, что находится в сосуде, не изменяется, то не изменится и сила давления на дно. Следовательно, уровень воды в сосуде останется прежним. Однако до того как лёд растаял, сила давления на дно определялась только силой давления воды, а после таяния льда она станет складываться из силы давления воды и силы давления свинца. Значит, давление воды станет меньшим, откуда следует, что уровень воды в сосуде понизится (в этом рассуждении не учтена сила атмосферного давления, но она здесь несущественна).
ЗАДАЧА № II.108В два колена U – образной трубки налиты вода и масло, разделённые ртутью (рис.81). Поверхности раздела ртути и жидкостей в обоих коленах находятся на одной высоте. Определить высоту столба воды, если высота столба масла 20 см.
Дано: 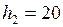 см
см 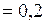 м.
м.
Найти: 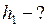
Решение
Согласно закону Паскаля, давление в обоих коленах трубки на уровне 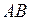 одинаково:
одинаково:
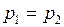 . (1)
. (1)
Здесь 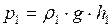 и
и 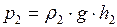 - давления в левом и правом коленах соответственно на уровне
- давления в левом и правом коленах соответственно на уровне  ;
;  и
и  - плотности воды и масла. Подставляя эти выражения в равенство (1), получаем:
- плотности воды и масла. Подставляя эти выражения в равенство (1), получаем:
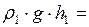
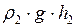 . (2)
. (2)
Выразим из равенства (2) высоту столба воды 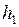 :
:
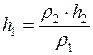 ;
; 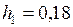 м.
м.
ЗАДАЧА № II.109Какова должна быть высота цилиндрического сосуда радиусом 5 см, заполненного водой, чтобы сила давления воды на дно сосуда была равна силе её давления на боковую поверхность?
Дано: 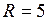 см
см 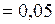 м
м
Найти: 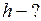
Решение
По определению, сила давления на дно сосуда:
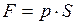 . (1)
. (1)
Так как давление на дно сосуда:
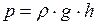 , (2)
, (2)
где 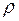 - плотность воды;
- плотность воды; 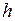 - высота сосуда.
- высота сосуда.
Площадь дна сосуда:
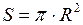 . (3)
. (3)
Подставим формулы (2) и (3) в формулу (1), получим:
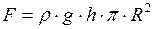 . (4)
. (4)
Аналогично, сила давления на боковую поверхность сосуда:
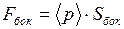 , (5)
, (5)
где 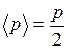 - среднее давление воды на боковую поверхность сосуда;
- среднее давление воды на боковую поверхность сосуда; 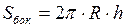 - площадь боковой поверхности сосуда. Учитывая, что
- площадь боковой поверхности сосуда. Учитывая, что 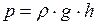 , получаем:
, получаем:
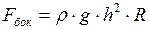 . (6)
. (6)
По условию задачи, 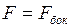 , или
, или
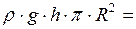
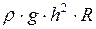 . (7)
. (7)
Выразим из равенства (7), высоту цилиндрического сосуда 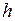 , получим:
, получим:
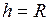 ;
; 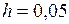 м.
м.
ЗАДАЧА № II.110По горизонтальной трубе переменного сечения течёт вода. Площади поперечных сечений трубы на разных её участках соответственно равны 10 см2 и 20 см2. Разность уровней воды в вертикальных трубках одинакового сечения составляет 20 см. Определите объём воды, проходящей за 1с через сечение трубы.
Дано: 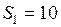 см2
см2 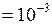 м2;
м2;
 см2
см2 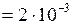 м2;
м2;
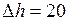 см
см 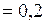 м;
м;
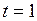 с
с
Найти: 
Решение
Запишем уравнение Бернулли для трубки тока, расположенной горизонтально:
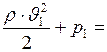
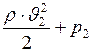 . (1)
. (1)
где 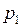 и
и 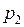 - статическое давление жидкости;
- статическое давление жидкости; 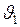 и
и 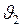 - скорость жидкости;
- скорость жидкости; 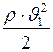 и
и 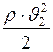 - динамическое давление жидкости для сечения трубки тока
- динамическое давление жидкости для сечения трубки тока 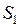 и
и 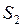 соответственно.
соответственно.
Найдём скорость 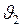 из уравнения неразрывности струи:
из уравнения неразрывности струи:
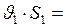
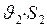 ;
; 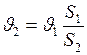 (2)
(2)
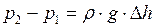 , (3)
, (3)
где 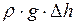 - гидростатическое давление.
- гидростатическое давление.
Подставим формулы (2) и (3), в формулу (1):
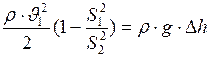 . (4)
. (4)
Выразим из формулы (4), скорость 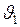 :
:
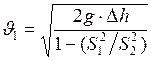 . (5)
. (5)
Тогда, объём воды, проходящей за 1с через сечение трубы 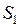 , можно будет найти по формуле:
, можно будет найти по формуле:
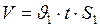 . (6)
. (6)
Подставим в формулу (6), формулу (5), получим:
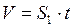
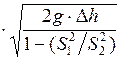 ;
; 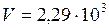 см3.
см3.
ЗАДАЧА № II.111Площадь соприкосновения слоев текущей жидкости 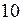 см2, коэффициент динамической вязкости жидкости
см2, коэффициент динамической вязкости жидкости 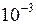 Па·с, а возникающая сила трения между слоями 0,1 мН. Определите градиент скорости.
Па·с, а возникающая сила трения между слоями 0,1 мН. Определите градиент скорости.
Дано: 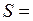
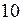 см2
см2 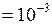 м2;
м2;
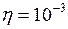 Па·с;
Па·с;
 мН =
мН = 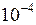 Н.
Н.
Найти: 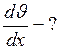
Решение
Сила внутреннего трения между слоями жидкости подчиняется закону Ньютона:
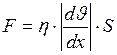 , (1)
, (1)
где 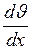 - градиент скорости;
- градиент скорости;  - площадь соприкосновения слоев текущей жидкости;
- площадь соприкосновения слоев текущей жидкости; 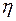 - коэффициент динамической вязкости жидкости;
- коэффициент динамической вязкости жидкости; 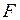 - сила трения между слоями.
- сила трения между слоями.
Из формулы (1) выразим градиент скорости, получим:
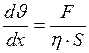 ;
; 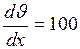 с-1.
с-1.
ЗАДАЧА № II.112Смесь свинцовых дробинок (плотность свинца- 11,3 г/см3) диаметром 4 мм и 2 мм одновременно опускают в широкий сосуд глубиной 1,5 м с глицерином (плотность глицерина - 1,26 г/см3, динамическая вязкость – 1,48 Па∙с) (рис.82). Определите, на сколько больше времени потребуется дробинке меньшего размера, чтобы достичь дна сосуда.
Дано:  г/см3
г/см3 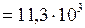 кг/м3;
кг/м3;
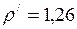 г/см3
г/см3 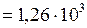 кг/м3;
кг/м3;
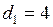 мм
мм 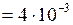 м;
м;
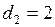 мм
мм 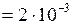 м;
м;
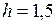 м
м
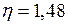 Па·с;
Па·с;
Найти: 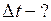
Решение
Чтобы определить, на сколько больше времени потребуется дробинке меньшего размера, чтобы достичь дна сосуда, необходимо воспользоваться формулой:
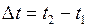 , (1)
, (1)
где 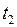 - время движения дробинки меньшего размера;
- время движения дробинки меньшего размера;
 - время движения дробинки большего размера.
- время движения дробинки большего размера.

Так как падение равномерное, то:
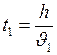 ;
; 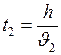 , (2)
, (2)
где 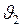 - скорость движения дробинки меньшего размера;
- скорость движения дробинки меньшего размера;
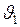 - скорость движения дробинки большего размера.
- скорость движения дробинки большего размера.
Найдём их. Для этого нам потребуется воспользоваться вторым законом динамики. Запишем его в векторной форме (рис.80):
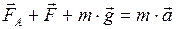 . (3)
. (3)
Проецируем обе части уравнения (3) на ось 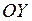 и учтём, что
и учтём, что 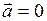 , т.к.
, т.к. 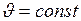 :
:
 , (4)
, (4)
где
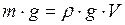 . (5)
. (5)
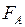 - сила Архимеда, она определяется по формуле:
- сила Архимеда, она определяется по формуле:
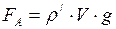 , (6)
, (6)
где 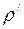 - плотность жидкости;
- плотность жидкости; 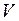 - объем погруженной в жидкость дробинки. Объём дробинки равен:
- объем погруженной в жидкость дробинки. Объём дробинки равен:
 . (7)
. (7)
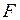 - сила сопротивления, действующая на медленно движущуюся в вязкой среде дробинку. Она определяется по формуле Стокса:
- сила сопротивления, действующая на медленно движущуюся в вязкой среде дробинку. Она определяется по формуле Стокса:
 , (8)
, (8)
где 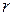 - радиус дробинки;
- радиус дробинки; 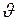 - её скорость;
- её скорость; 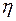 - динамическая вязкость жидкости.
- динамическая вязкость жидкости.
Подставим формулы (8), (7), (6) и (5) в формулу (4), получим:
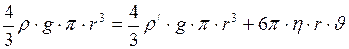 . (9)
. (9)
Преобразуем формулу (9) и выразим из неё скорость дробинки:
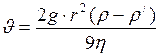 . (10)
. (10)
Учтём, что 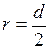 . Применим формулу (10) к нахождению скорости каждой из дробинок в отдельности, т.е.
. Применим формулу (10) к нахождению скорости каждой из дробинок в отдельности, т.е.  к
к 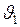 и
и 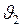 :
:
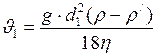 ;
; 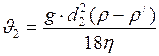 . (11)
. (11)
Подставим формулу (11) в формулу (2) и полученное выражение в формулу (1), после преобразований, получим:
 ;
; 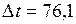 с.
с.
ЗАДАЧА № II.113В боковую поверхность цилиндрического сосуда 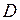 вставлен капилляр с внутренним диаметром
вставлен капилляр с внутренним диаметром 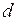 и длиной
и длиной 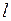 (рис.83). В сосуд налита жидкость с динамической вязкостью
(рис.83). В сосуд налита жидкость с динамической вязкостью 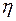 . Определите зависимость скорости понижения уровня жидкости
. Определите зависимость скорости понижения уровня жидкости 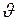 в сосуде от высоты
в сосуде от высоты 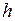 этого уровня над капилляром.
этого уровня над капилляром.
Дано: 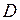 ,
, 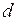 ,
, 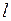 ,
, 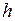 ,
, 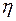
Найти: 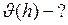
Решение
Объем жидкости, вытекающего за время 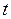 из сосуда через капилляр, определяется формулой Пуазейля:
из сосуда через капилляр, определяется формулой Пуазейля:
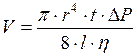 , (1)
, (1)
где 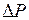 - разность давлений на концах капилляра, которая обусловлена гидростатическим давлением жидкости:
- разность давлений на концах капилляра, которая обусловлена гидростатическим давлением жидкости:
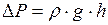 , (2)
, (2)
где 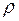 - плотность жидкости;
- плотность жидкости; 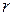 - радиус капилляра, он равен (
- радиус капилляра, он равен ( 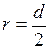 ).
).

Кроме того, объем вытекающей воды через капилляр за единицу времени может быть определён по формуле:
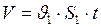 . (3)
. (3)
Для нахождения зависимость скорости понижения уровня жидкости 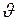 в сосуде от высоты
в сосуде от высоты 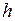 этого уровня над капилляром, воспользуемся уравнением неразрывности струи:
этого уровня над капилляром, воспользуемся уравнением неразрывности струи:
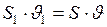 , (3)
, (3)
где 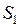 - площадь поперечного сечения капилляра. Она равна:
- площадь поперечного сечения капилляра. Она равна:
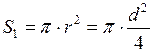 . (4)
. (4)
 - площадь поперечного сечения цилиндрического сосуда. Она равна:
- площадь поперечного сечения цилиндрического сосуда. Она равна:
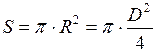 . (5)
. (5)
Подставим формулы (5) и (4) в формулу (3) и выразим из неё скорость 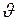 :
:
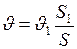 . (6)
. (6)
Скорость 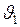 , найдём из равенства формул (1) и (3):
, найдём из равенства формул (1) и (3):
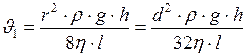 . (7)
. (7)
Подставим формулу (7), (4) и (5) в формулу (6), после преобразований получим:
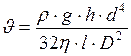 или
или  .
.
ЗАДАЧА № II.114Стальной шарик (плотность - 9 г/см3) диаметром 0,8см падает с постоянной скоростью в касторовом масле (плотность – 0,96 г/см3), динамическая вязкость 0,99 (Па · с). Учитывая, что критическое значение числа Рейнольдса 0,5, определите характер движения масла, обусловленный падением в нём шарика.
Дано: 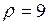 г/см3
г/см3 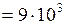 кг/м3;
кг/м3;
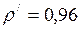 г/см3
г/см3 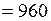 кг/м3;
кг/м3;
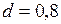 см
см 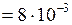 м;
м;
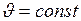 ;
;
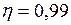 Па·с;
Па·с;
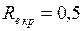
Найти: 
Решение

На стальной шарик, движущийся в касторовом масле с постоянной скоростью, действуют: сила Архимеда 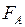 ; сила сопротивления
; сила сопротивления 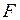 , действующая на движущейся в вязкой среде шарик и сила тяжести
, действующая на движущейся в вязкой среде шарик и сила тяжести 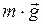 (рис.84).
(рис.84).
Запишем второй закон динамики в векторной форме:
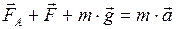 . (1)
. (1)
Проецируем обе части уравнения (1) на ось 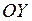 и учтём, что
и учтём, что 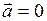 , т.к.
, т.к. 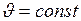 :
:
 , (2)
, (2)
где
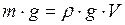 . (3)
. (3)
Сила Архимеда, определяется по формуле:
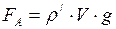 , (4)
, (4)
где 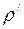 - плотность жидкости;
- плотность жидкости; 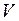 - объем погруженного в жидкость шарика. Объём шарика равен:
- объем погруженного в жидкость шарика. Объём шарика равен:
 . (5)
. (5)
Сила сопротивления, действующая на медленно движущийся в вязкой среде шарик, определяется по формуле Стокса:
 , (6)
, (6)
где 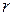 - радиус дробинки;
- радиус дробинки; 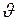 - её скорость;
- её скорость; 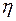 - динамическая вязкость жидкости.
- динамическая вязкость жидкости.
Подставим формулы (6), (5), (4) и (3), в формулу (2) и выразим из неё скорость, после преобразований, получим:
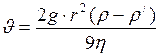 , (7)
, (7)
Или, учитывая, что 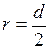 , формулу (7) можно переписать в виде:
, формулу (7) можно переписать в виде:
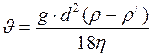 . (8)
. (8)
Для движения шарика в жидкости число Рейнольдса, определяется по формуле:
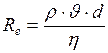 . (9)
. (9)
Подставим формулу (8), в формулу (9), получим:
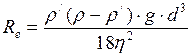 ;
; 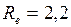 .
.
Так как 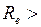
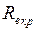 , то характер движения масла, обусловленный падением в нём шарика, буде турбулентным.
, то характер движения масла, обусловленный падением в нём шарика, буде турбулентным.
ЗАДАЧА № II.115Пустотелый медный шар весит в воздухе 17,8 Н, а в воде 14,2 Н. Определить объём полости, если плотность меди 8,9·103 кг/м3.
Дано: 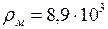 кг/м3;
кг/м3;
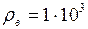 кг/м3;
кг/м3;
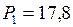 Н;
Н;
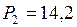 Н
Н
Найти: 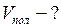
Решение
 а) б)
а) б)
|
В воздухе на шар действуют две силы: сила тяжести 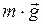 и сила реакции опоры
и сила реакции опоры  (рис.85,а). Запишем второй закон Ньютона в векторной форме:
(рис.85,а). Запишем второй закон Ньютона в векторной форме:
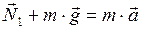 . (1)
. (1)
Проецируем обе части уравнения (1) на ось 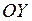 и учтём, что
и учтём, что 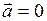 (тело находится в равновесии):
(тело находится в равновесии):
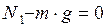 ,
, 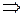
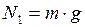 . (2)
. (2)
Массу шара определим по формуле:
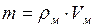 , (3)
, (3)
где 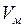 - объём стенок меди, он равен:
- объём стенок меди, он равен:
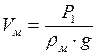 . (4)
. (4)
В воде на шар действуют три силы: сила тяжести 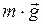 ; сила реакции опоры
; сила реакции опоры 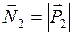 и выталкивающая сила
и выталкивающая сила 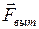 (рис.85,б). Запишем второй закон Ньютона в векторной форме (для случая, когда выполняется условие равновесия):
(рис.85,б). Запишем второй закон Ньютона в векторной форме (для случая, когда выполняется условие равновесия):
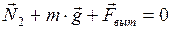 . (5)
. (5)
Проецируем обе части уравнения (5) на ось 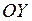 :
:
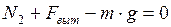 , (6)
, (6)
где
 . (7)
. (7)
Из уравнения (6) выталкивающая сила будет равна:
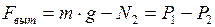 . (8)
. (8)
Подставим в формулу (8)  из формулы (7), получим:
из формулы (7), получим:
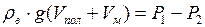 . (9)
. (9)
Выразим из равенства (9) объём полости 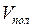 , после преобразований, получим:
, после преобразований, получим:
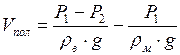 ;
; 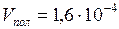 м3.
м3.
ЗАДАЧА № II.116Бревно высотой 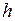 и площадью поперечного сечения
и площадью поперечного сечения  погружают в воду в вертикальном положении. Определить работу, которую совершила выталкивающая сила при полном погружении бревна (рис.86,а).
погружают в воду в вертикальном положении. Определить работу, которую совершила выталкивающая сила при полном погружении бревна (рис.86,а).
Дано:  ;
; 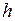 ;
; 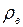 .
.
Найти: 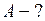
Решение
Выталкивающая сила равна:
 , (1)
, (1)
где 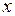 - глубина погружения бревна. Величина
- глубина погружения бревна. Величина 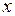 изменяется от 0 до
изменяется от 0 до 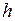 и, соответственно, выталкивающая сила, действующая на бревно, изменится от 0 до величины
и, соответственно, выталкивающая сила, действующая на бревно, изменится от 0 до величины 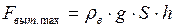 . На рисунке 86,б изображена зависимость величины выталкивающей силы от глубины погружения. Работа этой силы равна площади заштрихованного треугольника и определяется выражением:
. На рисунке 86,б изображена зависимость величины выталкивающей силы от глубины погружения. Работа этой силы равна площади заштрихованного треугольника и определяется выражением:
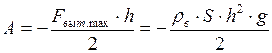 .
.
|

Знак минус означает, что выталкивающая сила направлена в сторону, противоположную перемещению. В случае подъёма бревна выталкивающая сила совершает положительную работу.
ЗАДАЧА № II.117Если на большой поршень с площадью  гидравлического пресса, заполненного жидкостью с плотностью
гидравлического пресса, заполненного жидкостью с плотностью 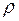 , надавить с силой
, надавить с силой 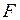 , то разность высот малого и большого поршней будет составлять
, то разность высот малого и большого поршней будет составлять 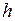 . Чему она будет равна (массой поршней пренебречь)?
. Чему она будет равна (массой поршней пренебречь)?
Дано:  ;
; 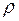 ;
; 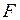
Найти: 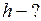
Решение
Дополнительное давление столба жидкости определим по формуле:
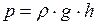 . (1)
. (1)
Давление, создаваемое силой 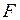 , равно:
, равно:
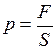 . (2)
. (2)
Приравняем формулы (1) и (2) и выразим 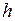 , получим:
, получим:
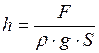 .
.
Дата добавления: 2016-09-06; просмотров: 7361;











