II.7. 2 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ЗАДАЧА № II.118Согласуется ли с принципами специальной теории относительности представление о теле в виде шара радиуса 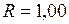м, вращающегося вокруг своей оси с угловой скоростью 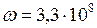рад/с?

Ответ. Нет, не согласуется. Скорость экваториальных точек такого тела 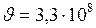м/с превышает скорость света в пустоте.

ЗАДАЧА № II.119Согласуется ли с принципами специальной теории относительности представление об электроне как о вращающемся вокруг своей оси однородном шарике массы 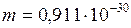кг (массы электрона) и радиуса 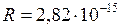м (классический радиус электрона), обладающем собственным моментом импульса 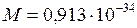(кг ∙ м²/с) (вытекающее из квантовой теории и подтверждённое экспериментально значение собственного момента импульса электрона)?

Ответ. Нет, не согласуется, так как скорость на «экваторе» такого шарика была бы равна 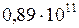м/с, т.е. превышала бы скорость света в пустоте почти в 300 раз.

ЗАДАЧА № II.120Имеются два одинаковых стержня. Стержень 1 покоится в системе отсчёта 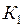, стержень 2 покоится в системе отсчёта 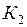. Системы движутся друг относительно друга вдоль совпадающих осей 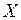. Стержни параллельны этим осям. Какой стержень будет короче: а) в системе 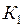, б) в системе ?

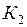Ответ. А)Стержень 2. Б) стержень 1.

ЗАДАЧА № II.121При каких условиях справедливы преобразования Галилея? преобразования Лоренца?

Ответ. Преобразования Галилея справедливы для скоростей, малых по сравнению со скоростью света в вакууме. Преобразования Лоренца справедливы и для скоростей, близких к скорости света в вакууме.

ЗАДАЧА № II.122Зависит ли от скорости движения системы отсчёта скорость тела? скорость света?

Ответ. Скорость тела зависит от выбора системы отсчёта; скорость света в вакууме не зависит от выбора системы отсчёта и во всех инерциальных системах отсчёта одинакова.

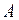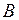ЗАДАЧА № II.123Неподвижный наблюдатель 1, находившийся посредине между точками и , увидел, что в эти точки одновременно попали молнии (рис. 87). Одновременны ли эти события для неподвижных наблюдателей 2 и 3? Для каких ещё неподвижных относительно 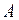и 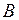наблюдателей, кроме наблюдателя 1, события в 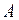и 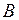будут одновременными?

Ответ. Нет. Для наблюдателя 2 в точку 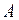молния попала раньше; для наблюдателя 3 молния попала раньше в точку 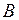. Для наблюдателей, равноудалённых от 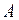и .

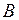ЗАДАЧА № II.124В тотмомент, когда середина поезда, движущегося равномерно и прямолинейно, проходит мимо наблюдателя 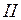, посредине перрона, одновременно для этого наблюдателя на концах перрона зажигаются фонар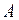и и 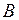(рис. 88). Одновременны ли эти события для наблюдателя 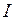, находящегося в середине движущегося поезда?

Ответ. Нет. Так как поезд движется в точке 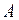, то свет от фонаря 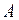до встречи с движущимся наблюдателем 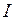должен пройти меньшее расстояние, чем свет от фонаря 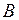. Следовательно, для движущегося наблюдателя раньше загорится фонарь .

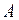ЗАДАЧА № II.125По условию задачи № II.118определить, какой фонарь для наблюдателя 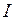загорится раньше, если фонари зажгли в тот момент, когда наблюдатель 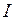находился (рис.90): 1) в точке 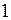; 2) в точке 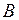; 3) в точке 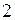. Где должен находиться наблюдатель 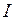в момент зажигания фонарей, чтобы свет из точек 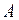и 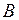пришёл к нему одновременно?

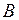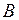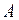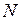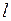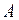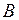Ответ: 1) фонарь ; 2) фонарь ; 3) фонарь . Наблюдатель должен находиться в точке на таком расстоянии от середины перрона, чтобы к моменту прохождения наблюдателем середины перрона свет из и , одновременно пришёл в точку 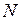: 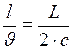, 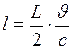(рис.89).

ЗАДАЧА № II.126Какой стала бы длина тела по направлению движения относительно неподвижного наблюдателя при ?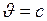

Ответ. Из формулы 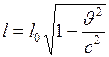следует, что при 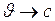, 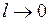. Следовательно, при 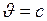длина тела стала бы равной нулю, что невозможно.

ЗАДАЧА № II.127Что можно сказать о длине стержня в различных инерциальных системах отсчёта? Имеет ли смысл понятие «длина стержня» вне связи с системой отсчёта?

Ответ. Длина стержня в различных системах отсчёта неодинакова. Понятие длины стержня имеет смысл только в конкретной системе отсчёта.

ЗАДАЧА № II.128Какую скорость должно иметь тело, чтобы его продольные размеры уменьшились для неподвижного наблюдателя 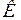в 3 раза? До этого тело покоилось относительно данного наблюдателя.

Дано: ;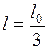

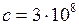м/с.

Найти: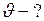

Решение

Относительно наблюдателя 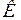продольные размеры движущегося тела изменяются:

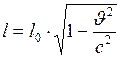, (1)

где 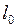- длина покоящегося тела.

Выразим из уравнения (1) скорость движения тела, предварительно возведя обе части равенства в квадрат, получим:

; ,

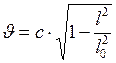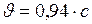т.е. скорость тела должна составлять 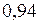скорости света. Поперечные размеры тела при этом не меняются.

ЗАДАЧА № II.129Какова должна быть энергия частицы, чтобы её продольный размер стал в 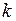раз меньше поперечного?

Дано: ;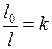

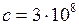м/с.

Найти: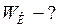

Решение

Кинетическая энергия частицы определяется по формуле:

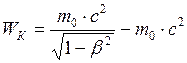. (1)

Преобразуем уравнение (1) к виду:

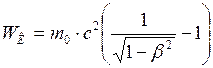. (2)

Относительно наблюдателя 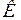продольные размеры движущегося тела изменяются:

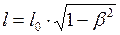. (3)

Выразим из формулы (3) 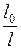, по условию задачи: 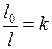, следовательно,

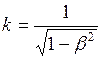. (4)

Подставим формулу (4), в формулу (2), получим:

.

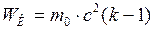ЗАДАЧА № II.130При какой относительной скорости движения релятивистское сокращение длины движущегося тела составляет 25%.

Дано: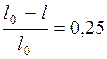

Найти: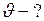

Решение

Относительно наблюдателя 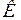продольные размеры движущегося тела изменяются:

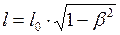. (1)

По условию задачи 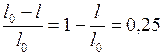. Отсюда, следует, что 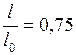, или 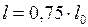. Подставим это значение в формулу (1), получим: 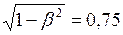. Значит .

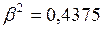Таким образом,

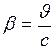, следовательно,

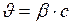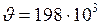; км/с.

ЗАДАЧА № II.131Ракета движется относительно неподвижного наблюдателя 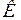со скоростью, равной 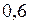скорости света в вакууме. Какое время пройдёт по часам неподвижного наблюдателя, если по часам, движущимся вместе с ракетой, прошло 6 лет?

Дано: ;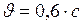

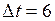лет;

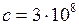м/с.

Найти: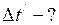

Решение

Время, прошедшее по часам неподвижного наблюдателя, найдём по формуле:

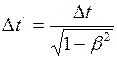. (1)

где - интервал времени, между событиями, отсчитанный движущимися вместе с телом часами;

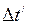- интервал времени, между теми же событиями, отсчитанный покоящимися часами;

.

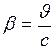В данной задаче время можно не выражать в секундах, а оставить в годах.

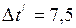лет.

ЗАДАЧА № II.132Собственное время жизни частицы отличается на 1% от времени жизни по неподвижным часам. Определите .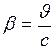

Дано: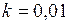

Найти: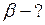

Решение

Релятивистское замедление хода часов определяется по формуле:

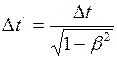, (1)

где - интервал времени, между событиями, отсчитанный движущимися вместе с телом часами;

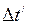- интервал времени, между теми же событиями, отсчитанный покоящимися часами;

Собственное время жизни частицы отличается от времени жизни по неподвижным часам на величину 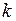равную:

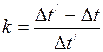. (2)

Перепишем формулу (2) в виде:

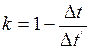. (3)

Выразим 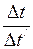из формулы (1) и подставим в формулу (3):

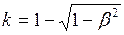. (4)

Из формулы (4), определим :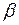

;

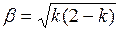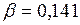
ЗАДАЧА № II.133Определите зависимость скорости частицы (масса частицы 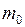) от времени, если движение одномерное, сила постоянна и уравнение движения релятивистское.

Дано: ; .

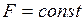Найти: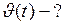

Решение

Для нахождения зависимости скорости движения частицы от времени, используем основной закон релятивистской динамики:

, ,

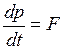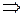
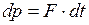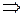
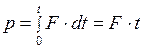. (1)

Релятивистский импульс частицы определяется формулой:

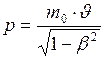. (2)

Приравняем формулы (1) и (2):

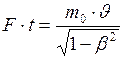. (3)

Выразим из полученного равенства скорость 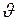, после преобразований получим:

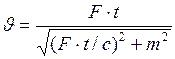. (4)

Формула (4) и будет устанавливать зависимость скорости движения частицы от времени .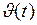

ЗАДАЧА № II.134Определите релятивистский импульс и кинетическую энергию протона, движущегося со скоростью .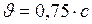

Дано: 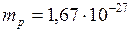кг;

.

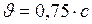Найти: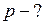

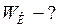
Решение

Релятивистский импульс протона определим по формуле:

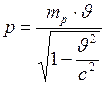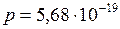; (Н·с).

Кинетическая энергия 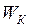протона будет равна:

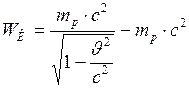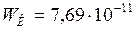; Дж.

ЗАДАЧА № II.135Определите работу, которую необходимо совершить, чтобы увеличить скорость частицы от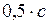до .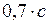

Дано: .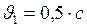

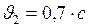
Найти: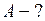

Решение

Работу, которую необходимо совершить, для увеличения скорости частицы, найдём из уравнения:

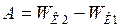, (1)

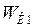где и 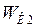- начальная и конечная кинетическая энергия частицы. Они соответственно равны:

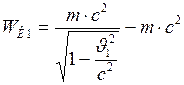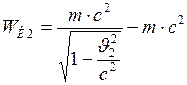и . (2)

Подставим формулу (2) в формулу (1), получим:

; .

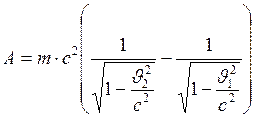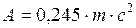ЗАДАЧА № II.137С какой скоростью достигают электроны анода рентгеновской трубки, работающей при напряжении 50 кВ? Решить задачу с учётом релятивистской поправки и найти процент ошибки при расчёте, произведённом по классическим формулам.

Дано: 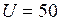кВ.

Найти: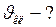

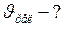
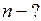
Решение

Согласно классическим формулам, из закона сохранения энергии имеем:

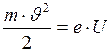. (1)

Из формулы (1), найдём :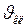

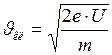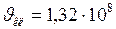; м/с.

Согласно релятивистским формулам, из закона сохранения энергии имеем:

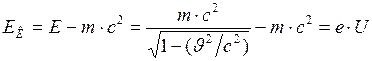. (2)

Отсюда

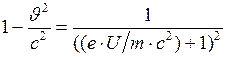. (3)

Из равенства (3), найдём :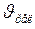

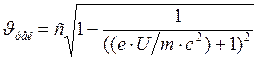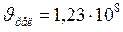; м/с.

Процент ошибки 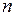можно определить по формуле:

.

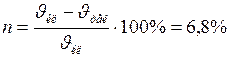ЧАСТЬ III. ВОПРОСЫ И ЗАДАНИЯ ДЛЯ САМОПРОВЕРКИ