Алгоритм и этапы решения задачи

Пример 1. Пусть реализуется проект по асфальтированию участка земли под АТС, при этом привлекаемые рабочие могут выполнять любую из выделенных по принятой технологии работ. Менеджер проекта установил, что в данном проекте от начала до завершения ра-бот можно выделить пять событий и существуют шесть различных видов работ, связывающих эти события. При первоначальном распределении рабочих по видам работ на основе имеющихся нормативов трудоемкости были рассчитаны длительности выполнения работ (в днях). Таким образом, сетевой график реализации данного проекта имеет вид модели, представленной на рис. 19.1

Требуется рассчитать основные характеристики событий, работ и всей сетевой модели в целом, а также определить наличие резерва времени для некоторых работ в целях оптимизации модели и со­кращения сроков выполнения проекта за счет перераспределения рабочих по видам работ.

Решение. Рассмотрим этапы табличного метода расчета данной сетевой модели. Результаты расчетов приведены в табл. 5.3 в графах 1—9.

Пояснения

Этап 1. Перечень работ и их продолжительность запишем в гр. 2 и 3 табл. 5.3, при этом работы записываются последовательно в гр. 2: сначала — начинающиеся с номера 1, затем с ном.2 и т.д.

Этап2 . В первой графе поставим число Kпр, показывающее количество работ, непосредственно предшествуюших событию i, с которого начинается рассматриваемая работа . Для работ , начинающихся с номера 1 предшествующих работ нет . Для работы , начи­нающейся с номера к, просматриваются все верхние строки второй гра-фы и отыскиваются работы, начинающиеся на к . Количество найденных работ записывается во все строки гр.1, которые соответствуют рабо-там, начинающимся с номера k Например, для работы (4, 5) в гр. 1 поставим цифру 2, так как на номер 4 оканчиваются две работы: (1, 4) и (3, 4).

Этап 3. Заполнение таблицы начинается с расчета раннего срока работ tp(i). Для работ, имеющих цифру «НОЛь» в первой гра­фе, в гр. 4 также заносятся нули и рассчитываются соответствую­щие значения гр. 5 (ранний срок окончании tро(I,j) как суммы соответствующих чисел в гр. 2 и 3 (см. формулу (5.41)). В нашей мо­дели таких работ три; в первой строке гр. 5 ставим 6 + 0 = 6, ана­логично во второй и третьей строках.

Для заполнения следующих строк гр. 4. для работ (i,j)просмат­риваются заполненные строки гр. 5, котОрые содержат работы, оканчивающиеся на номер i, и максимальНое из наИденных значе­ний (если их несколько) переносится в гр 4 для обрабатываемых строк. Так, в нашем примере в четвертой строке в гр. 4 ставим 6, а гр 5

15 (9 + 6 = 15).

Аналогично в пятой строке гр. 4 и 5 ставим соответственно 5 и 17

(12 + 5 = 17).

В последней, шестой, строке гр. 4 ставим 17 (наибольшее из чисел 8 и 17 в гр 5) и соответствен­но в гр. 5 ставим 21 (4 + 17 = 21).

Этап 4. Графы 7 и 6 заполняются «обратным ходом», т.е. снизу вверх. Для этого просматриваются строки (работы), оканчи­вающиеся на номер N последнего события , и из гр.5 выбирается величина. Эта величина записывается в гр. 7 по всем строкам, оканчивающимся на N (см. формулу (5.42) с учетом ра­венства tn(N) = tp(N)). Затем заполняется гр. 6 по этим строкам как разность между гр. 7 и 3 (см. формулу (5.43)).

В нашем примере таких строк две (четвертая и шестая), в гр. 5 стоят числа 15 и 21; выбираем наибольшее из них (21) и записываем его в гр. 7 по этим строкам, после чего заносим соответствующие числа в гр. 6.

Далее просматриваются строки, оканчивающиеся на номер со­бытия, предшествующего заверша-ющему, т.е. на (N — 1). Для этих строк просмат-риваются все строки гр. 6, лежащие ниже и начинающиеся с номера (N — 1). Среди них в гр. 6 выбирается минимальная величина, которая переносится в гр. 7 по обрабатываемым строкам, после чего заполняется гр. 6. В нашем примере таких строк две (третья и пятая); ниже их с номера 4 начинается одна (последняя) работа, и в гр. 6 стоит 17, следовательно, в гр. 7 по этим строкам ставим число 17, после чего заполняется гр. 6.

Затем аналогичный процесс повторяется для строк, оканчивающихся на (N — 2), (N — 3) и т д., до тех пор, пока не будут заполнены все строки по гр. 7 и 6. В нашем примере результаты приведены в соответствующих графах табл. 5.3.

Этап 5. Показатели гр. 8 рассчитываются как разности соответствующих показателей гр. 6 и 4 или гр. 7 и 5 (см. формулы (5.39) или (5.44)). Чтобы заполнить гр. 9, можно предварительно рассчитать резервы времени каждого события по формуле (5.39), а затем воспользоваться формулой (5.46). В нашем примере резервы времени для каждого из пяти событий равны соответственно: R(1) = 0; R(2) = 12 - 6 = 6; R(3) = 5-5 = 0; R(4) = 17 - 17 = 0; R(5) = 0. Последующие результаты по формуле (5.46) приведены в гр. 9 табл. 5.3.

Этап 6. На этом этапе подводятся основные итоги расчета. Учитывая, что нулевой резерв времени имеют только работы (Rn = 0) и события (R(i) = 0), принадлежащие критичес-кому пути, получаем, что критическим является путь LKp = (1, 3, 4, 5), продолжитель­ность которого (tкр) равна 21 дню.

Так как работы (1, 2), (1, 4) и (2, 5) имеют ненулевые резервы Rn, то очевидно, что путем перевода некоторого числа рабочих с этих работ на работы, принадлежащие критиче-кому пути, можно сократить продолжитель-ность этого пути и тем самым сократить сроки выполнения проекта в целом.

Сети Петри. Сети Петри — математический аппарат для моделирования динамических дискретных систем.

Впервые описаны Карлом Петри в 1984 году.

Сеть Петри представляет собой двудольный ориентированный граф, состоящий из вершин двух типов — позиций и переходов, соединённых между собой дугами, вершины одного типа не могут быть соединены непосредственно. В позициях могут размещаться метки (маркеры), способные перемещаться по сети.

Событием называют срабатывание перехода, при котором метки из входных позиций этого перехода перемещаются в выходные позиции. События происходят мгновенно, либо разновременно, при выполнении некоторых условий.

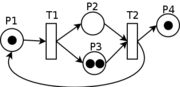
Пример сети Петри. Белыми кружками обозначены позиции, полосками — переходы, чёрными кружками — метки.

Некоторые виды сетей Петри:

• Временная сеть Петри — переходы обладают весом, определяющим продолжительность срабатывания (задержку).
• Стохастическая сеть Петри — задержки являются случайными величинами.
• Функциональная сеть Петри — задержки определяются как функции некоторых аргументов, например, количества меток в каких-либо позициях, состояния некоторых переходов.
• Цветная сеть Петри — метки могут быть различных типов, обозначаемых цветами, тип метки может быть использован как аргумент в функциональных сетях.
• Ингибиторная сеть Петри — возможны ингибиторные дуги, запрещающие срабатывания перехода, если во входной позиции, связанной с переходом ингибиторной дугой, находится метка.
• Иерархическая сеть — содержит не мгновенные переходы, в которые вложены другие, возможно, также иерархические, сети. Срабатывание такого перехода характеризует выполнение полного жизненного цикла вложенной сети.
• WF-сети

Основными свойствами сети Петри являются:

• ограниченность — число меток в любой позиции сети не может превысить некоторого значения K;
• безопасность — частный случай ограниченности, K=1;
• сохраняемость — постоянство загрузки ресурсов, 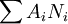постоянна. Где N_i — число маркеров в i-той позиции, A_i — весовой коэффициент;
• достижимость — возможность перехода сети из одного заданного состояния (характеризуемого распределением меток) в другое;
• живость — возможность срабатывания любого перехода при функционировании моделируемого объекта.

В основе исследования перечисленных свойств лежит анализ достижимости.

Сети Петри - это аппарат для моделирования динамических дискретных систем (преимущественно асинхронных параллельных процессов). Сеть Петри определяется как четверка <Р, Т, I, О>, где Р и Т - конечные множества позиций и переходов, I и О -множества входных и выходных функций. Другими словами, сеть Петри представляет собой двудольный ориентированный граф, в котором позициям соответствуют вершины, изображаемые круж­ками, а переходам - вершины, изображаемые утолщенными чер­точками; функциям I соответствуют дуги, направленные от пози­ций к переходам, а функциям О - дуги, направленные от переходов к позициям.

Как и в системах массового обслуживания, в сетях Петри вво­дятся объекты двух типов: динамические, которые изображаются метками (маркерами) внутри позиций, и статические, которым соответствуют вершины сети Петри.

Распределение маркеров по позициям называют маркировкой. Маркеры могут перемещаться в сети. Каждое изменение маркиров­ки называют событием, причем каждое событие связано с опреде­ленным переходом. Считается, что события происходят мгновенно и разновременно при выполнении некоторых условий.

Каждому условию в сети Петри соответствует определенная позиция. Совершению события соответствует срабатывание (воз­буждение или запуск) перехода, при котором маркеры из входных позиций этого перехода перемещаются в выходные позиции. Последовательность событий образует моделируемый процесс.

Правила срабатывания переходов (рис. 2.8) конкретизируют следующим образом: переход срабатывает, если для каждой из его входных позиций выполняется условие N_i> К_i, где N_i - число маркеров в i-й входной позиции, K_i - число дуг, идущих от i-й пози­ции к переходу; при срабатывании перехода число маркеров в i-й входной позиции уменьшается на К_i, а в j-й выходной позиции уве­личивается на М_j ,где М_j - число дуг, связывающих переход с j-й позицией.

На рис. 19.2. показан пример распределения маркеров по позициям перед срабатыванием, эту маркировку записывают в виде (2, 2, 3, 1) или (2231). После срабатывания перехода маркировка принимает вид (1,0,1,4).

Можно вводить ряд дополнительных правил и условий в алгоритмы моделирования, получая ту или иную разновидность сетей Петри. Так, прежде всего полезно ввести модельное время, чтобы моделировать не только последовательность событий, но и их привязку ко времени. Это осуществляется приданием переходам веса - продолжительности (задержки) срабатывания, которую можно определять, используя задаваемый при этом алгоритм. Полученную модель называют временной сетью Петри..

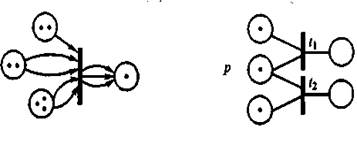
Рис. 19.2. Фрагмент сети Петри Рис. 19.3. Конфликтная ситуация

Если задержки являются случайными величинами, то сеть на­зывают стохастической. В стохастических сетях возможно вве­дение вероятностей срабатывания возбужденных переходов. Так, на рис. 2.9 представлен фрагмент сети Петри, иллюстрирующий конфликтную ситуацию - маркер в позиции p может запустить либо переход t₁ ,либо переход t₂. В стохастической сети предусматрива­ется вероятностный выбор срабатывающего перехода в таких си­туациях.

Если задержки определяются как функции некоторых аргумен­тов, которыми могут быть количество маркеров в каких-либо по­зициях, состояния некоторых переходов и т.п., то сеть называют функциональной.

Во многих задачах динамические объекты могут быть несколь­ких типов, и для каждого типа нужно вводить свои алгоритмы по­ведения в сети. В этом случае каждый маркер должен иметь хотя бы один параметр, обозначающий тип маркера. Такой параметр обычно называют цветом; цвет можно использовать как аргумент в функциональных сетях. Сеть Петри при этом называют цветной.

Среди других разновидностей сетей Петри следует упомянуть ингибиторные сети, характеризующиеся тем, что в них возможны запрещающие (ингибиторные) дуги. Наличие маркера во входной позиции, связанной с переходом ингибиторной дугой, означает запрещение срабатывания перехода.

Введенные понятия поясним на следующих простых примерах.

Пример 1. Требуется описать с помощью сети Петри функционирование системы из предприятий A, В и С. Предприятия А и В поставляют узлы Х1 и X2 соответственно, а на предприя­тии С происходит сборка, в каждый сборочный узел входит один узел X1 и два узла X2. На рис. 2.10 предприятиям А, В и С соответствуют переходы t₁, t₂ и t₃.

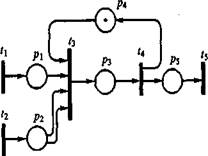
Рис. 19.4 Сеть Петри для примера 1

Срабатывание перехода t₃ происходит только в том слу­чае, если, во-первых, в позиции p_l имеется метка, а в позиции р₂ - не менее двух меток, что
означает поступление от пред-приятии А и В соответствующих комплектующих, и, во-вторых, имеется метка в позиции p₄, что означает, что предприятие С закончило сборку предыдущего изделия и готово приступить к сборке следующего. Пока очередное изделие не будет собрано, метки в p₄ не будет, следовательно, запросы, пришедшие во входные позиции р₁ и р₂, вынуждены ожидать срабатывания перехода t₄. Переходам t₁, t₂ и t₃ поставлены в соответствие процедуры вычисления задержек срабатывания. Задержки в первых двух переходах равны интервалам времени между появлениями готовых узлов, задержка в t₃ равна времени сборки изделия.

Пример 2. Требуется описать с помощью сети Петри процес­сы возникновения и устранения неисправностей в некоторой техни­ческой системе, состоящей из М однотипных блоков; в запасе име­ется один исправный блок; известны статистические данные об интенсивностях возникновения отказов и длительностях таких опе­раций, как поиск неисправностей, замена и ремонт отказавшего блока. На рис. 2.11 представлена соответствующая сеть Петри. Отметим, что при числе меток в позиции, равном М, можно в ней не ставить М точек, а записать в позиции значение М.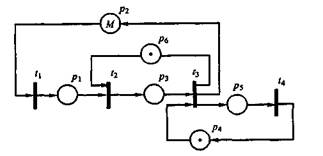

Рис. 2.11. Сеть Петри для примера 2

В нашем примере значение M в позиции р₂ соответствует числу имеющихся в системе блоков. Переходы отображают следующие события: t₁ - отказ блока, t₂- поиск неисправного блока, t₃ - его за­мена, t₄ - окончание ремонта.

Очевидно, что при непустой позиции р_г переход t₁ срабатывает, но с задержкой, равной вычисленному случайному значению мо­делируемого отрезка времени между отказами. После выхода маркера из t₁ он попадает через р₁ в t₂, если имеется метка в пози­ции р₆, это означает, что обслуживающая систему бригада специа­листов свободна и может приступить к поиску возникшей неисп­равности. В переходе t₂ метка задерживается на время, равное случайному значению длительности поиска неисправности. Далее маркер оказывается в р₃ и если имеется запасной блок (маркер в р₄), то запускается переход t₃, из которого маркеры выйдут в р₂ , р₅ и р₆ через отрезок времени, требуемый для замены блока. После этого в t₄ имитируется восстановление неисправного блока.

Рассматриваемая модель описывает функционирование систе­мы в условиях, когда отказы могут возникать и в рабочем, и в неисправном состояниях системы. Поэтому не исключены ситуа­ции, при которых более чем один маркер окажется в позиции р₁.

Марковские случайные процессы. Названы по имени выдающегося русского математика А.А.Маркова , впервые начавшего изучение вероятностной связи случайных величин и создавшего теорию, которую можно назвать "динамикой вероятностей". В настоящее время теория марковских процессов и ее приложения широко применяются в самых различных областях и , в том числе, в исследовании операций и теории принятия оптимальных решений.

Марковский процесс— дискретный или непрерывный случайный процесс X(t), который можно полностью задать с помощью двух величин:

· вероятности P(x,t) того, что случайная величина x(t) в момент времени t равна x, и

· вероятности P(x₂, t₂|x₁,t₁) того, что если x при t = t₁ равен x₁, то при t = t₂ он равен x₂.

Вторая из этих величин называется вероятностью перехода из состояния x₁ при t = t₁ в состояние x₂ при t = t₂.

Цепями Маркова называют дискретные по времени и значению Марковские процессы .

Пример 1. Предположим, что речь идет о последовательных бросаниях монеты при игре "в орлянку "; монета бросается в условные моменты времени t = 0, 1, ... и на каждом шаге игрок может выиграть ±1 с одинаковой вероятностью 1/2, таким образом в момент t его суммарный выигрыш есть случайная величина ξ(t) с возможными значениями j = 0, ±1, ... При условии, что ξ(t) = k, на следующем шаге выигрыш будет уже равен ξ(t+1) = k ± 1, принимая указанные знчения j = k ± 1 c одинаковой вероятностью 1/2. Условно можно сказать, что здесь с соответствующей вероятностью происходит переход из состояния ξ(t) = k в состояние ξ(t+1) = k ± 1.

Формулы и определения Марковских цепей. Обобщая этот пример, можно представить себе "систему" со счетным числом возможных "фазовых" состояний, которая с течением дискретного времени t = 0, 1, ... случайно переходит из состояния в состояние.

Пусть ξ(t) есть ее положение в момент t в результате цепочки случайных переходов ξ(0) - ξ(1) - ... - ξ(t) - ... ... (1)

Формально обозначим все возможные состояния целыми i = 0, ±1, ... Предположим, что при известном состоянии ξ(t) = k на следующем шаге система переходит в состояние ξ(t+1) = j с условной вероятностью

p_kj = P(ξ(t+1) = j|ξ(t) = k) ... (2)

независимо от ее поведения в прошлом, точнее, независимо от цепочки переходов (1) до момента t:

P(ξ(t+1) = j|ξ(0) = i, ..., ξ(t) = k) = P(ξ(t+1) = j|ξ(t) = k) при всех t, k, j ... (3) - марковское свойство.

Такую вероятностную схему называют однородной цепью Маркова со счетным числом состояний - ее однородность состоит в том, что определенные в (2) переходные вероятности p_kj, ∑_j p_kj = 1, k = 0, ±1, ..., не зависят от времени, т.е.

P(ξ(t+1) = j|ξ(t) = k) = P_ij - матрица вероятностей перехода за один шаг не зависит от n. Ясно, что P_ij - квадратная матрица с неотрицатель-ными элементами и единичными суммами по строкам. Такая матрица (конечная или бесконечная) называется стохастической матрицей. Любая стохастическая матрица может служить матрицей переходных вероятностей.