Дифференциальное уравнение теплопроводности.

При выводе дифференциального уравнения теплопроводности сделаны следующие допущения:
- тело однородно и изотропно;
- физические параметры постоянны;
- деформация рассматриваемого объема, связанная с изменением температуры, является очень малой величиной по сравнению с самим объемом;
- внутренние источники теплоты в теле, которые в общем случае могут быть заданы как q_v=f(x, у, z, t), распределены равномерно.

В основу вывода дифференциального уравнения теплопроводности положен закон сохранения энергии, который в рассматриваемом случае может быть сформулирован следующим образом:количество теплоты dQ₁, введенное в элементарный объем извне за время dt вследствие теплопроводности, а также от внутренних источников, равно изменению внутренней энергии или энтальпии вещества (в зависимости от рассмотрения изохорического или изобарического процесса), содержащегося в элементарном объеме:

где dQ₁ — количество теплоты, Дж, введенное в элементарный объем путем теплопроводности за время dt,
dQ₂ — количество теплоты, которое за время dt выделилось в элементарном объеме dv за счет внутренних источников;
dQ—изменение внутренней энергии или энтальпии вещества, содержащегося в элементарном объеме dv, за время dt.

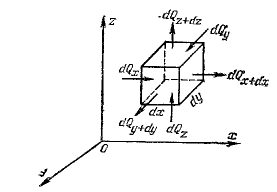
Для нахождения составляющих уравнения (1) выделим в теле элементарный параллелепипед со сторонами dx, dy, dz (рис.1). Параллелепипед расположен так, чтобы его грани были параллельны соответствующим координатным плоскостям.
Количество теплоты, которое подводится к граням элементарного объема за время dt в направлении осей Ox, Оу, Oz, обозначим соответственно dQ_x, dQ_y, dQ_zКоличество теплоты, которое будет отводиться через противоположные грани в тех же направлениях, обозначим соответственно dQ_x+dx, + dQ_y+dy, + dQ_z+dz. Количество теплоты, подведенное к грани dydz в направлении оси Ох за время dt, составляет dOx=q_xdydzdt, где q_x —проекция плотности теплового потока на направление нормали к указанной грани. Количество теплоты, отведенное через противоположную грань элементарного параллелепипеда в направлении оси Ох, запишется как

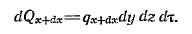
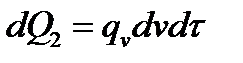Определим вторую составляющую уравнения (1). Обозначим количество теплоты, выделяемое внутренними источниками в единице объема среды в единицу времен и называемое мощностью внутренних источников теплоты, через q_v, Вт/м³, тогда

Третья составляющая в уравнении (1) будет определена в зависимости от характера термодинамического процесса изменения системы.
При рассмотр

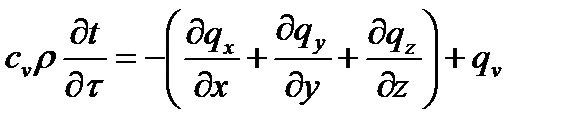ении изохорного процесса вся теплота, подведенная к элементарному объему, уйдет на изменение внутренней энергии вещества, заключенного в этом объеме, т.е. dQ = dU.
Если рассматривать внутреннюю энергию единицы объема u=u(t, v), тогда dU определится как

где С_v – изохорная теплоемкость единицы объема, Дж/м³×К; c_v - изохорная теплоемкость единицы массы, Дж/кг×К, r - плотность вещества, кг/м³.

Это выражение является дифференциальным уравнением энергии для изохорного процесса переноса теплоты.

Выражение (5) называется дифференциальным уравнением теплопроводности. Оно устанавливает связь между временным и пространственным изменениями температуры в любой точке тела, в котором происходит процесс теплопроводности.

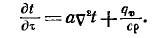
Коэффициент пропорциональности а, [м²/с], в уравнении называетсякоэффициентом температуропроводности иявляется физическим параметром вещества.Он существенен для нестационарных тепловых процессов и характеризует скорость изменения температуры.Если коэффициент теплопроводности характеризует способность тел проводить теплоту, то коэффициент температуропроводности является мерой теплоинерционных свойств тела. Из уравнения следует, что изменениетемпературы во времени для любой точкипространства пропорционально величине a.

Иначе говоря, скорость изменения температуры в любой точке тела будет тем больше, чем больше коэффициент температуропроводности.Поэтому при прочих равных условиях выравнивание температур во всех точках пространства будет происходить быстрее в том теле, которое обладает большим коэффициентом температуропроводности. Коэффициент температуропроводности зависит от природы вещества. Например, жидкости и газы обладают большой тепловой инерционностью и, следовательно, малым коэффициентом температуропроводности.