Неравенство Клаузиуса. Энтропия. Тепловой поток. Виды тепл-х Потоков.
Предположим, что рассматриваемое тело может обмениваться теплотой лишь с N бесконечными тепловыми резервуарами, внутренняя энергия которых столь велика, что при рассматриваемом процессе температура каждого остаётся строго постоянной. Предположим, что над телом был совершён произвольный круговой процесс, то есть по окончании процесса оно находится абсолютно в том же состоянии, что и в начале.
Пусть при этом за весь процесс оно заимствовало из i-го резервуара, находящегося при температуре Ti, количество теплоты Qi. Тогда верно следующее неравенство Клаузиуса:
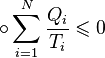
Здесь обозначает круговой процесс.
В общем случае теплообмена со средой переменной температуры неравенство принимает вид
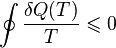
Здесь dQ(T) — количество теплоты, переданное участком среды с (постоянной) температурой T. Это неравенство применимо для любого процесса, совершаемого над телом. В частном случае квазистатического процесса оно переходит в равенство. Математически это означает, что для квазистатических процессов можно ввести функцию состояния, называемую энтропией, для которой
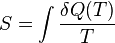
здесь T — это абсолютная температура внешнего теплового резервуара. В этом смысле 1/Т является интегрирующим множителем для количества теплоты.
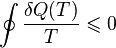
Здесь dQ(T) — количество теплоты, переданное участком среды с (постоянной) температурой T. Это неравенство применимо для любого процесса, совершаемого над телом. В частном случае квазистатического процесса оно переходит в равенство
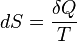 Математически это означает, что для квазистатических процессов можно ввести функцию состояния, называемую энтропией, для которой
Математически это означает, что для квазистатических процессов можно ввести функцию состояния, называемую энтропией, для которой
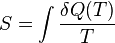
здесь T — это абсолютная температура внешнего теплового резервуара. В этом смысле 1/Т является интегрирующим множителем для количества теплоты.
Для неквазистатических процессов такое определение энтропии не работает. Например, при адиабатическом расширении газа в пустоту 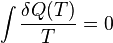
однако энтропия при этом возрастает, в чём легко убедиться, переведя систему в начальное состояние квазистатически и воспользовавшись неравенством Клаузиуса. Кроме того, энтропия (в указанном смысле) не определена для неравновесных состояний системы, хотя во многих случаях систему можно считать локально равновесной и обладающей некоторым распределением энтропии.
Квазистатический процесс в термодинамике —идеализированный процесс, состоящий из непрерывно следующих друг за другом состояний равновесия.
Квазистатические процессы не реализуются в природе, но являются хорошей моделью для приближения процессов, протекающих достаточно медленно (для квазистатического процесса скорость изменения макроскопического параметра должна удовлетворять условию ,
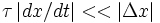 где t — время релаксации, — характерный масштаб изменения величины ).
где t — время релаксации, — характерный масштаб изменения величины ).
Квазистатические процессы всегда обратимы. Это следует из того, что любое промежуточное состояние есть состояние термодинамического равновесия, а оно не зависит от того, идет процесс в прямом или обратном направлении. При круговых квазистатических процессах энтропия системы не меняется.
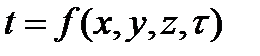
 Процесс теплопроводности неразрывно связан с распределением температуры внутри тела. Температурное поле. Температура, как известно, характеризует тепловое состояние тела и определяет степень его нагретости. Так как тепловое состояние отдельных частей тела в процессе теплопроводности различно, то в общем случае температура t является функцией координат х, у, z и времени t, т. е.
Процесс теплопроводности неразрывно связан с распределением температуры внутри тела. Температурное поле. Температура, как известно, характеризует тепловое состояние тела и определяет степень его нагретости. Так как тепловое состояние отдельных частей тела в процессе теплопроводности различно, то в общем случае температура t является функцией координат х, у, z и времени t, т. е.
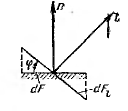
Направление вектора плотности теплового потока совпадает с направлением распространения теплоты в данной точке и противоположно направлению вектора температурного градиента.
Рис. 1. К расчету теплового потока.
Плотность теплового потока- количество теплоты Qi, проходящее через элементарную площадку dFi,
расположенную под углом j к плоскости, касательной к
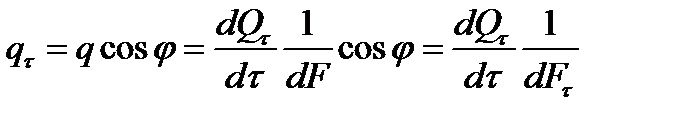 изотермической поверхности в единицу времени
изотермической поверхности в единицу времени
(рис. 1), определяется:
Так как dF=dFlcosj является проекцией площадки dFl, на изотермическую поверхность, то количество теплоты, протекающее через элементарную площадку dFl за время dt, запишется как
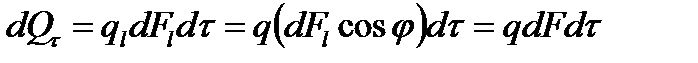
Дата добавления: 2021-06-28; просмотров: 643;











