Стационарные процессы теплопроводности (аналитическое описание процесса). Коэффициент теплопередачи.

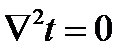
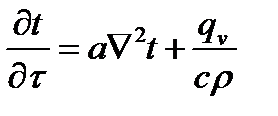При установившемся, или стационарном, тепловом режиме температура тела во времени остается постоянной, т. е.
При этом дифференциальное уравнение теплопроводности имеет вид:
(2.1)

Если внутренние источники теплоты отсутствуют (q_v=0), то уравнение (2.1) упростится и примет вид:

а) Граничные условия первого рода
Рассмотрим однородную и изотропную стенку толщиной d с постоянным коэффициентом теплопроводности l. На наружных поверхностях стенки поддерживают постоянными температуры t_с1 и t_с2.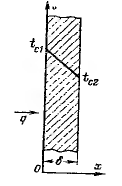
При заданных условиях температура будет изменяться только в направлении, перпендикулярном плоскости стенки. Если ось Ох направить, как показано на рис. 2.1, то температура в направлении осей Оу и Oz будет оставаться постоянной:

Для определения количества теплоты, проходящего через единицу поверхности стенки в единицу времени в направлении оси Ох, воспользуемся законом Фурье. Учитывая, что после подстановки значения в выражение закона Фурье получим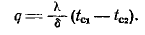

Из уравнения (2.9) следует, что количество теплоты,проходящее через единицу поверхности стенки в единицу времени, прямо пропорционально коэффициенту теплопроводности l, разности температур на наружных поверхностях стенки t_C1 — t _С2 и обратно пропорционально толщине стенки d. Следует указать, что тепловой поток определяется не абсолютным значением температур, а их разностью t_C1 — t_С2 = Dt которую принято называть температурным напором.
Отношение l/d, Вт/(м2×К)называется тепловой проводимостью стенки,а обратная величина d/l, м²×К/Вт— тепловым или термическим сопротивлением стенки.Последнее представляет собой падение температуры в стенке на единицу плотности теплового потока. Зная плотность теплового потока, легко вычислить общее количество теплоты Qt, которое передается через поверхность стенки величиной F за промежуток времени t:

б) Граничные условия третьего рода (теплопередача)
Передача тепла из одной подвижной среды (жидкости или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы называется теплопередачей. Теплопередача включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной подвижной среде.
Рассмотрим теплопередачу через однородную и многослойную плоские стенки.
Пусть плоская однородная стенка имеет толщину d (рис. 2.3) Заданы коэффициенты теплопроводности стенки l температуры окружающей среды t_ж1 и t_ж2, а также коэффициенты теплоотдачи a₁ и a₂; будем считать, что величины t_ж1, t_ж2, a₁ и a₂ постоянны, и не меняются вдоль поверхности. Это позволяет рассматривать изменение температуры жидкостей и стенки только в направлении, перпендикулярном плоскости стенки.

При заданных условиях необходимо найти тепловой поток от горячей

жидкости к холодной и температуры на поверхностях стенки.

\

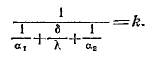
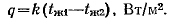
Величина k имеет ту же размерность, что и a, и называется коэффициентом теплопередачи.Коэффициент теплопередачи k характеризуетинтенсивность передачи теплоты от одной жидкости к другой через разделяющую их стенку и численно равен количеству теплоты, которое передается через единицу поверхности стенки в единицу времени при разности температур между жидкостями в один градус.
Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением теплопередачи.