Инерционная девиация первого рода

Рассматривая инерционную девиацию первого рода, будем считать, что масляный успокоитель имеет одинаковое количество жидкости в обоих сосудах и возможность ее перетекания из сосуда в сосуд исключена. В этом случае его влиянием на движение гиросферы можно пренебречь и полагать, что силы инерции приложены только к центру масс гиросферы так, как это показано на рис. 2.12 б.

При оговоренных условиях сила инерции f₂, возникающая вследствие наличия ускорения 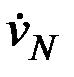, будет определяться следующим равенством:

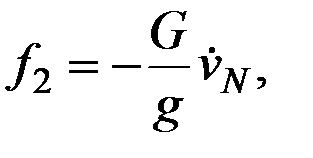(2.24)
где 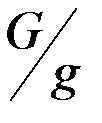- масса гиросферы. В свою очередь, выражение для момента силы f₂ относительно оси ОЕ примет вид:

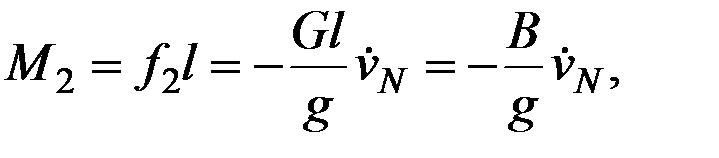(2.25)
где 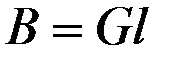. Под действием момента М₂ гиросфера начнет прецессировать вокруг оси Оn с угловой скоростью

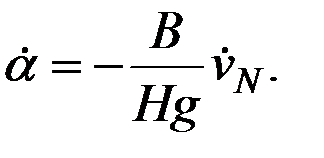(2.26)
Если принять, что судно начало маневрировать в некоторый момент времени t₁, когда северная составляющая его скорости была равна v_N1, а закончило маневр в момент времени t₂, имея скорость v_N2, угол поворота гиросферы за время маневра можно определить следующим выражением:

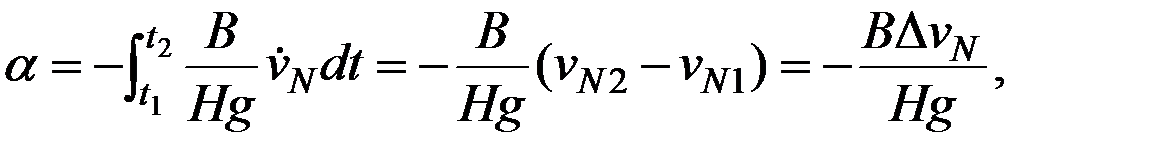(2.27)
где 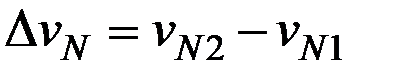- изменение северной составляющей скорости судна за время маневра.

В свою очередь, изменение значения северной составляющей скорости судна вызовет изменение положения компасного меридиана. Для оценки этого изменения обратимся к первому равенству (2.27), которое запишем несколько в ином виде:

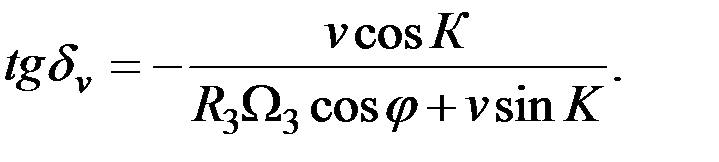(2.28)
Заменим в последнем равенстве истинный курс судна К компасным курсом К’. Для этого учтем, что

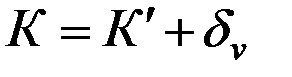(2.29)
Подставляя (2.29) в равенство (2.28) найдем:

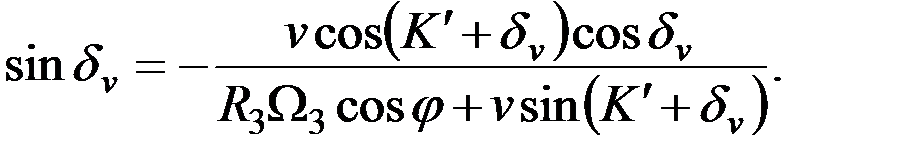(2.30)
Последнее равенство перепишем в следующем виде:

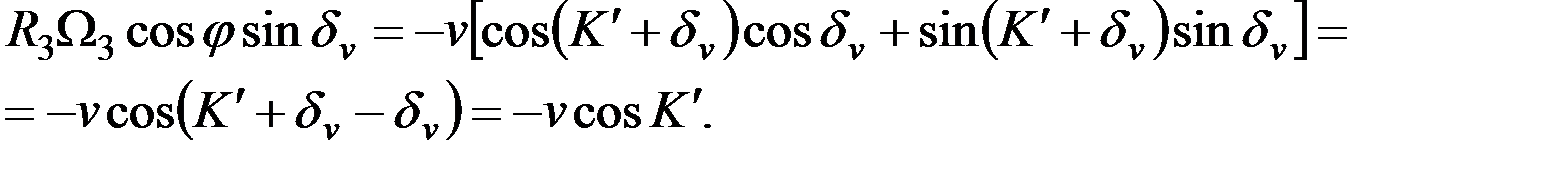(2.31)
Отсюда вытекает, что

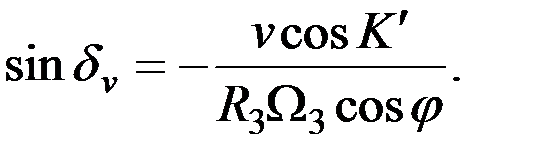(2.32)

Учитывая, что величина скоростной девиации, как правило, невелика, положение компасного меридиана N_k1 (рис. 2.13) до начала маневра можно определить по приближенной формуле

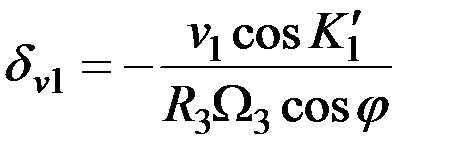. (2.33)

В направлении этого компасного меридиана будет ориентирована главная ось гиросферы (вектор ее кинетического момента Н₁) до начала маневра судна.

Положение компасного меридиана в конце маневра будет определяться углом

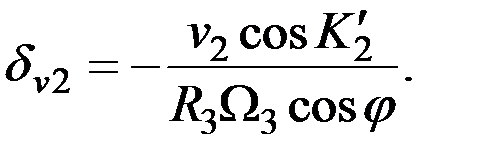(2.34)
Поскольку это положение соответствует устойчивому равновесию главной оси гиросферы после маневра, то величина инерционной девиации гирокомпаса определяется текущим углом 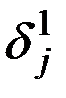отклонения ее вектора кинетического момента от этого положения. Как следует из рисунка

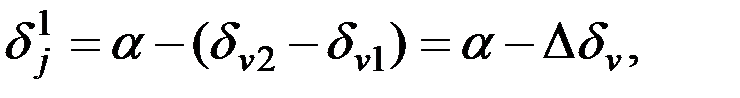(2.35)
где 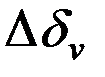- разница скоростных девиаций в конце и начале маневра.

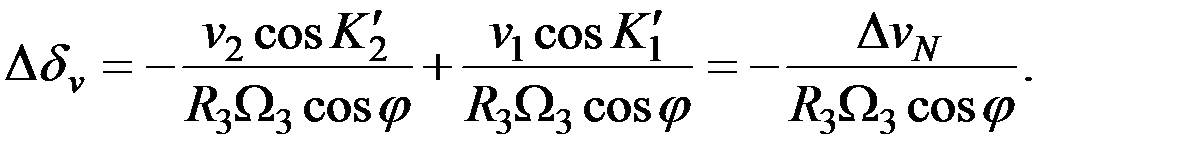(2.36)
Здесь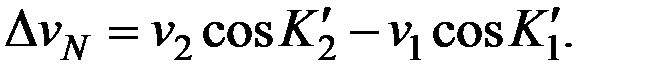

После прекращения судном маневра главная ось гиросферы начнет устанавливаться в новое положение компасного меридиана, совершая, как и при включении ГК, затухающие колебания относительно этого положения. На рис. 2.13 они представлены кривой α(t).

Уместно заметить, что инерционная девиация будет равна нулю, и никаких колебаний гиросферы происходить не будет, если в конце маневра ее главная ось окажется в положении, совпадающим с новым компасным меридианом. Такой переход гиросферы в новое устойчивое положение получил название апериодического перехода. Постараемся выяснить условия, при выполнении которых он имеет место.

Аналитически эти условия выглядят следующим образом:

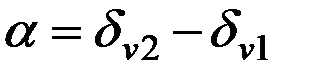(2.37)
или

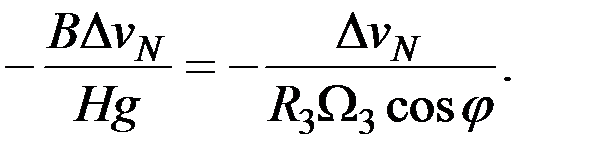(2.38)
Перепишем выражение (2.38) в несколько ином виде

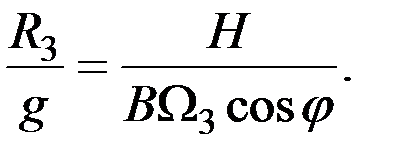(2.39)
Извлекая из левой и правой частей равенства (2.39) квадратные корни и умножая их на 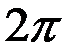, найдем:

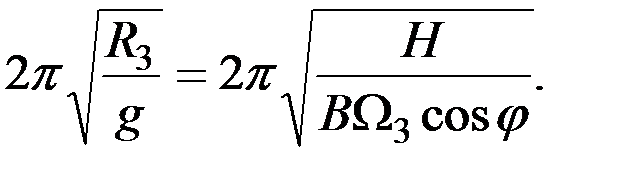(2.40)
Нетрудно заметить, что в правой части равенства (2.40) стоит выражение, определяющее период Т₀ незатухающих колебаний гиросферы (см. равенство 1.18). В свою очередь

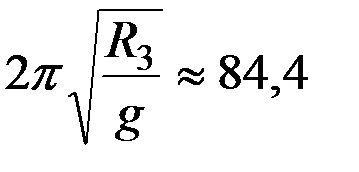мин. (2.41)
Учитывая это, окончательно условие апериодических переходов может быть записано в следующем виде

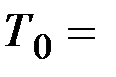
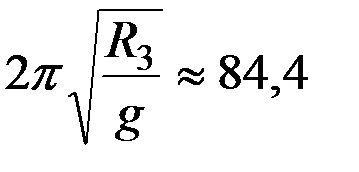мин. (2.42)

Указанное условие было найдено немецким ученым М. Шулером (1882 –1972) и получило его имя. Замечательной особенностью этого условия является то, что оно не зависит от параметров маневра судна и, тем самым, открывает хорошие возможности для его практической реализации. Однако в силу того, что период колебаний гиросферы не постоянный, а зависит от широты места судна, если не регулировать значения В или Н, это условие выполнимо только для какой-нибудь одной широты, которую называют расчетной широтой. Так, в гирокомпасах “Курс” эти условия выполнены для расчетной широты 60⁰.

Были также разработаны апериодические ГК, в основном для часто маневрирующих военных судов. В этих гирокомпасах при изменении широты места судна за счет разведения гироскопов гиросферы ее кинетический момент изменялся таким образом, чтобы выполнялись условия (2.42). Указанным путем удавалось исключить инерционную девиацию первого рода в определенном диапазоне широт.

В том случае, если ГК для какой-то широты настроен на период Шулера, то вне этой широты его инерционная девиация будет определяться следующими выражениями:

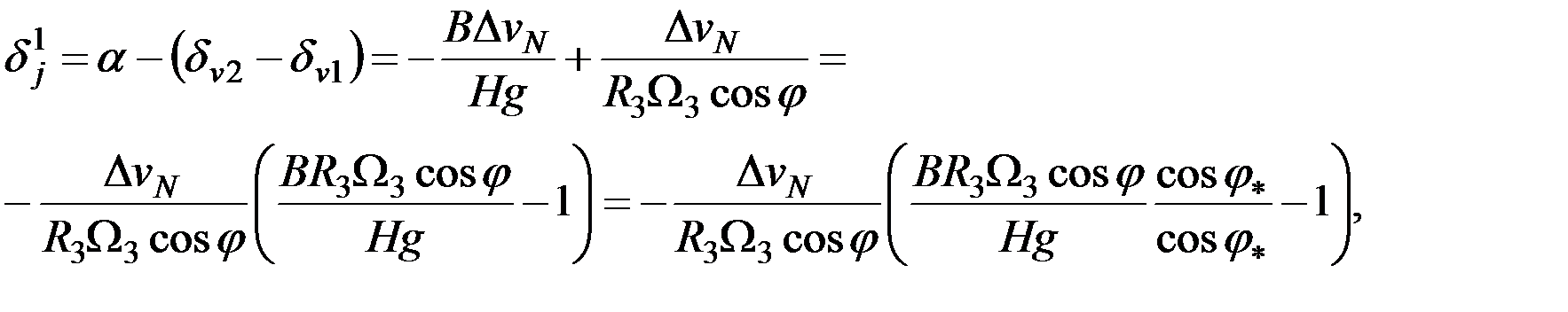(2.43)
где 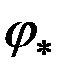- расчетная широта. Полученные соотношения могу быть существенно упрощены если учесть, что в соответствии с условиями Шулера (2.40) в расчетной широте имеет место следующее равенство:

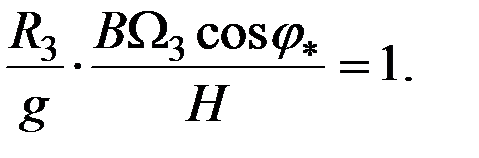(2.44)
Использование этого равенства, позволяет записать окончательное выражение для рассматриваемой инерционной девиации ГК:

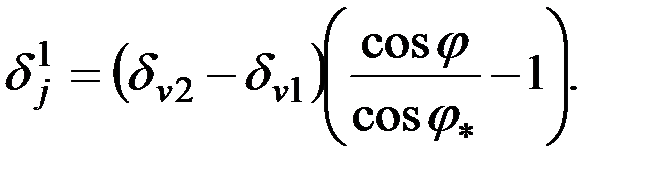(2.45)

Подводя итог проведенному анализу, сформулируем основные особенности инерционной девиации первого рода:

§

Важно!

инерционная девиация имеет место всегда, когда судно маневрирует не в расчетной широте;

§ максимальное значение девиация достигает в конце маневра после чего, изменяясь по гармоническому закону, постепенно затухает;

§ максимальное значение девиации пропорционально разности скоростей в начале и конце маневра и растет с удалением от расчетной широты;

§ инерционные девиации в широтах, разнесенных относительно расчетной, имеют разные знаки.

§ 2.5.2. Инерционная девиация второго рода

Как было отмечено выше, инерционная девиация второго рода возникает за счет того, что силы, порождаемые ускорениями при маневрировании судна, воздействуют на гидравлический успокоитель колебаний гиросферы и, тем самым, порождают дополнительные моменты, приложенные к ней. Максимальное влияние на уровень этих моментов оказывают составляющие ускорения движения судна, лежащие в плоскости меридиана. Так, при наличии ускорения 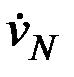(рис. 2.14), силы инерции, воздействуя на частицы жидкости, заставят их смещаться в южном направлении, что приведет к появлению разницы Δh ее уровней в сосудах, причем в южном сосуде уровень будет более высоким. В этих условиях в процессе маневра на гиросферу будут действовать два момента М₁ и М₂, порождаемые силами инерции. Влияние первого, обусловленного силой f , приложенной к центру масс гиросферы, было рассмотрено в предыдущем параграфе. Этот момент порождает девиацию первого рода. Момент М₂ силы Р_ж, возникает за счет наличия избыточной массы жидкости, в данном случае, в южном сосуде, и, как это следует из рисунка, направлен в сторону, противоположную моменту М₁. Учитывая, что именно этот момент порождает девиацию второго рода, рассмотрим его влияние на поведение гиросферы более подробно. Будем для простоты считать, что судно находится в расчетной широте, в которой отсутствует девиация первого рода. Тогда, если бы не было возможности перетекания жидкости из сосуда в сосуд и, тем самым, не было бы момента М₂, угловая скорость прецессии гироскопа была бы такой, что в конце маневра главная ось гиросферы, (вектор Н₂ рис. 2.15), оказалась бы совмещенной с положением компасного меридиана N_k2, соответствующего северной составляющей скорости судна в конце маневра. Однако в силу того, что существует момент М₂, скорость прецессии гиросферы будет меньше и за время маневра она, повернувшись на угол α, займет положение, определяемой вектором Н_к.м.. Отклонение указанного вектора от направления компасного меридиана N_k2 определит значение инерционной девиации второго рода 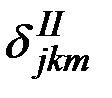в конце маневра.

После того как маневр закончится сила f и ее момент М₁ исчезнут и гиросфера останется только под действием момента М₂, который будет постепенно убывать по мере выравнивания уровней жидкости в северном и южном сосудах. В результате она начнет прецессировать в противоположном направлении, что вызовет увеличение ее отклонения от компасного меридиана N_k2 и, как следствие, увеличение инерционной девиации второго рода. Как правило, постоянная времени гидравлического маятника, определяющая скорость выравнивания уровней жидкости в сосудах, достаточно велика. Так, для гирокомпаса “Курс” она составляет 667 секунд. Это означает, что в течении относительно длительного промежутка времени девиация второго рода будет постепенно нарастать пока не достигнет своего максимума, соответствующего точке т на кривой переходного процесса 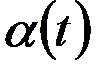. В этой точке отклонение вектора кинетического момента Н_т гиросферы от направления меридиана N_k2, будет соответствовать максимальному значению инерционной девиации второго рода.

После того, как девиация достигнет своего максимума, гиросфера начнет устанавливаться в компасный меридиан N_k2, совершая около него затухающие колебания, показанные на рисунке кривой .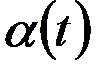

Таким образом, в отличие от инерционной девиации первого рода, достигающей своего максимума в конце маневра, рассматриваемая девиация максимальна спустя некоторое время после окончания маневра. Для гирокомпасов “Курс” это время соответствует примерно 15 минутам.

Для устранения инерционной девиации второго рода можно на время маневра отключать затухание, перекрывая возможность перетекания жидкости из сосуда в сосуд.