Типовая схема гирокомпаса

<36 373839 40 41 42 >

Двухгироскопные компасы, сочетая в себе такие качества, как относительно низкая стоимость изделий и высокая надежность, имеют один существенный недостаток, заключающийся в отсутствии возможности коррекции параметров движения и положения гиросферы. От этого недостатка свободны рассматриваемые гирокомпасы, поскольку здесь оператор имеет возможность прикладывать специально сформированные управляющие моменты непосредственно к его чувствительному элементу. Указанная возможность сделала приборы рассматриваемого типа весьма перспективными, открывающими дорогу для интенсивного использования новейших достижений электроники и вычислительной техники с целью наиболее полного удовлетворения требований практики.

Простейшая схема гирокомпаса с корректируемым чувствительным элементом представлена на рис. 3.1. В его основе лежит астатический гироскоп с тремя степенями свободы. Для того чтобы этот гироскоп приобрел способность устанавливаться в меридиан, он должен быть снабжен устройством, которое воздействовало бы на него так же, как воздействует на гиросферу двухгироскопного компаса ее маятниковость. Иными словами, при отклонении главной оси ох гироскопа от плоскости горизонта относительно оси оу внутренней рамки карданова подвеса должен создаваться момент, пропорциональный этому углу отклонения.

Указанная задача решается контуром коррекции, включающим в себя акселерометр А, усилитель У_у, сумматор С_у и датчик моментов ДМ_у. При отсутствии маневрирования судна, выходной сигнал акселерометра будет пропорциональным проекции ускорения силы тяжести Земли на направление его оси чувствительности. В силу того, что он устанавливается на внутренней рамке карданова подвеса таким образом, чтобы эта ось была параллельна главной оси гироскопа, выходной сигнал акселерометра будет пропорционален углу отклонения плоскости рамки, а, следовательно, и главной оси гироскопа от плоскости горизонта. В силу указанных обстоятельств этот прибор часто называют индикатором горизонта.

Сигнал акселерометра после усиления в усилителе У_у поступает на датчик моментов ДМ_у, который прикладывает к гироскопу момент, пропорциональный напряжению, поступившему на него, которое, в свою очередь, пропорционально указанному выше углу отклонения главной оси гироскопа. Таким образом, создается модель физического маятника, присутствующего в двухгироскопном компасе.

Следует отметить, что указанный способ создания маятникового момента обладает, как минимум, двумя существенными преимуществами перед физическим маятником. Так, при наличии ускорений, обусловленных качкой судна и его маневрированием, их влияние на работу гирокомпаса с неуравновешенным чувствительным элементом пропорционально той силе инерции, приложенной к его центру массы, которую они порождают. В результате имеет место практически линейная зависимость 1 (рис. 3.2) между моментами сил инерции, приложенными к гироскопу, и указанными уско 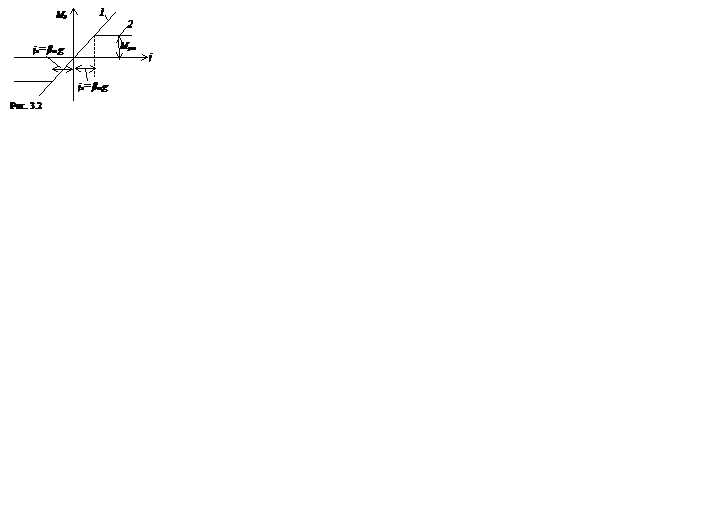рениями. При использовании акселерометра, имеющего характеристику 2, котораялинейна только в диапазоне относительно небольших значений ускорений, соизмеримых с величиной 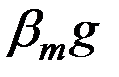, где 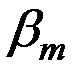- максимально возможное отклонение главной оси гироскопа от плоскости горизонта, g – ускорение силы тяжести, степень влияния вредных ускорений будет существенно снижена.

Второе преимущество указанной системы коррекции состоит в том, что на время маневра судна, когда влияние вредных ускорений достаточно ощутимо, особенно если речь идет о высокоскоростных судах, имеется возможность полного отключения коррекции.

Для обеспечения демпфирования прецессионных колебаний гироскопа в процессе его установления в меридиан имеется второй контур коррекции, включающий в себя акселерометр А, усилитель У_z, датчик моментов ДМ_z. Этот контур создает относительно оси оz наружной рамки подвеса момент, пропорциональный углу отклонения главной оси от плоскости горизонта. Приложенный момент вызывает прецессию оси гироскопа в сторону плоскости горизонта, в результате чего и обеспечивается требуемое затухание.

Наряду с указанным выше, рассматриваемая схема гирокомпаса допускает создание внешних корректирующих сигналов U_ky и U_kz, которые используются для устранения систематических ошибок гирокомпаса как методических, так и инструментальных.

Съем информации о курсе судна осуществляется датчиком курса ДК.

Следует отметить, что приведенная схема корректируемого гирокомпаса является предельно упрощенной, но позволяющей корректно выявить основные его свойства. Все необходимые уточнения будут рассмотрены ниже на моделях гирокомпасов, более близких к реальным изделиям. Уравнения движения чувствительного элемента гирокомпаса

Как и ранее, для выяснения основных свойств гирокомпаса рассматриваемого типа составим уравнения, описывающие движение его чувствительного элемента. Для этого обратимся к зависимостям (2.20 [56]), описывающим поведение гироскопа с тремя степенями свободы на подвижном основании при воздействии на него внешних возмущающих моментов М_х и М_у. Учитывая незначительное влияние нутационных колебаний на работу гирокомпаса, опустим из рассмотрения первые слагаемые этих зависимостей, определяющие указанные колебания. В результате названные выражения примут вид:

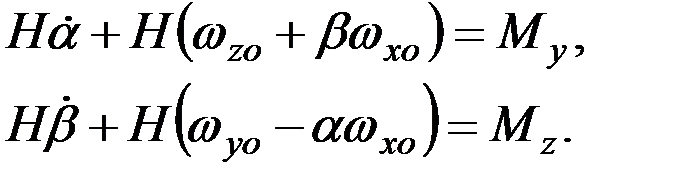(3.1)

Подставим в эти уравнения выражения (2.38 [56]), определяющие угловые скорости движения основания гирокомпаса. В результате получим:

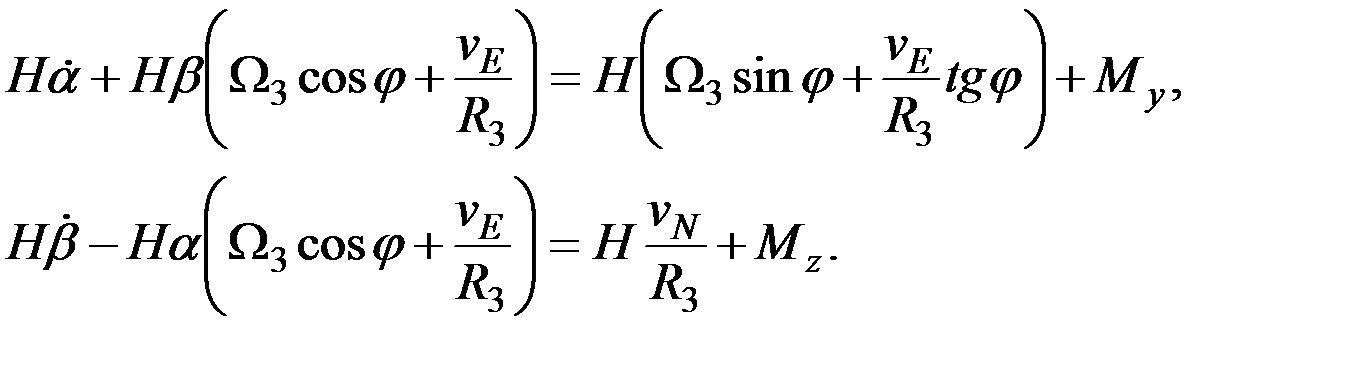(3.2)

Если считать гироскоп с технологической точки зрения идеальным, т.е. не имеющим инструментальных погрешностей, то моменты М_х и М_у будут создаваться только датчиками моментов ДМ_у и ДМ_z. Величина этих моментов пропорциональна напряжениям, поступающим на них, а знак выбирается таким, чтобы движение гироскопа было устойчивым. Учитывая это можно записать:

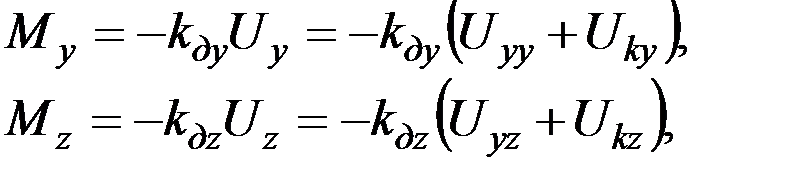(3.3)
где U_y и U_z – напряжения, поступающие на статорные обмотки датчиков моментов; U_yy и U_yz – выходные напряжения усилителей У_у и У_z, соответственно; U_ky и U_kz – сигналы коррекции гироскопа, формируемые внешними системами коррекции с целью компенсации систематических ошибок прибора.

Учитывая, что

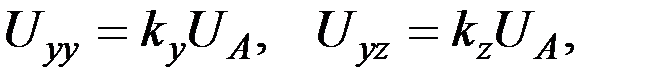(3.4)
где k_y и k_z – коэффициенты усиления усилителей У_уи У_z, а U_A – выходное напряжение акселерометра, выражения (3.3) перепишем в виде:

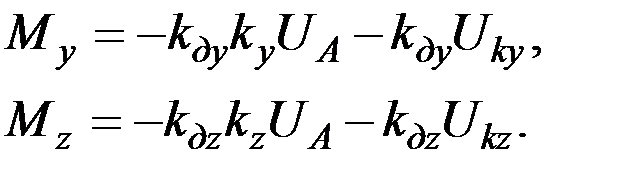(3.5)
Подставляя равенства (3.5) в уравнения (3.2), найдем:

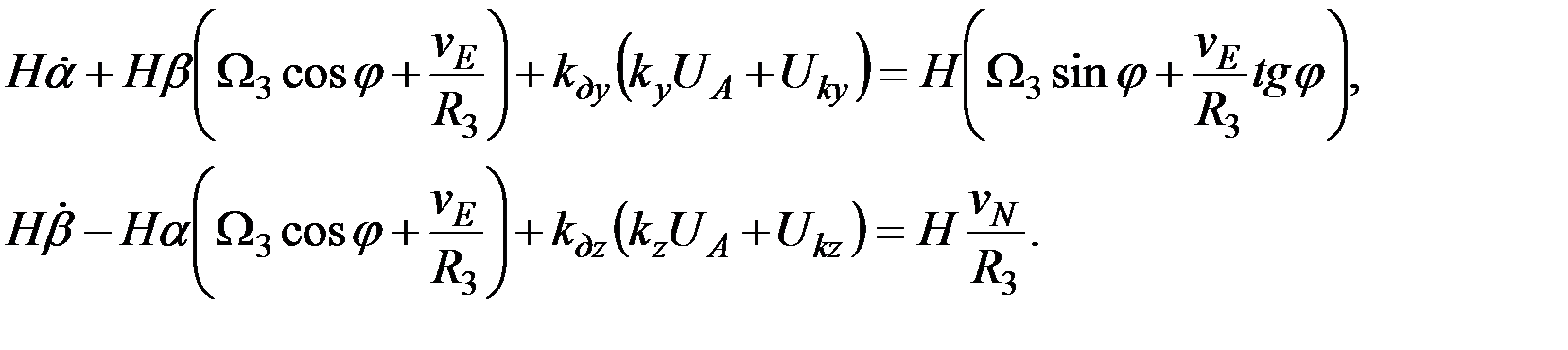(3.6)
На практике всегда выполняется неравенство

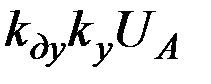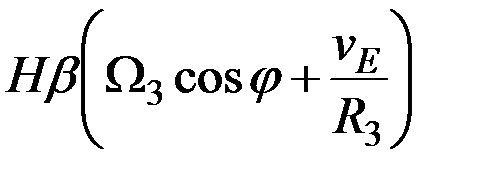>> . (3.7)

Это позволяет последние уравнения переписать в более простой форме:

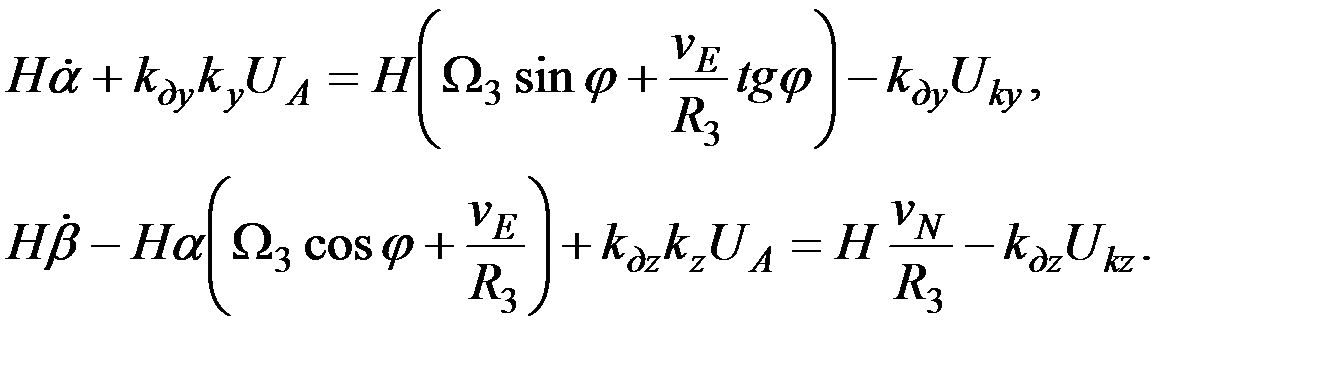(3.8) Как видим, полученные уравнения содержат неизвестную U_A, которая должна быть дополнительно определена. Это можно сделать, воспользовавшись уравнением (4.7 [56]) акселерометра, установленного на внутренней рамке карданова подвеса.

Объединяя зависимости (3.8) и (4.7), запишем искомые уравнения корректируемого гирокомпаса в окончательном виде: 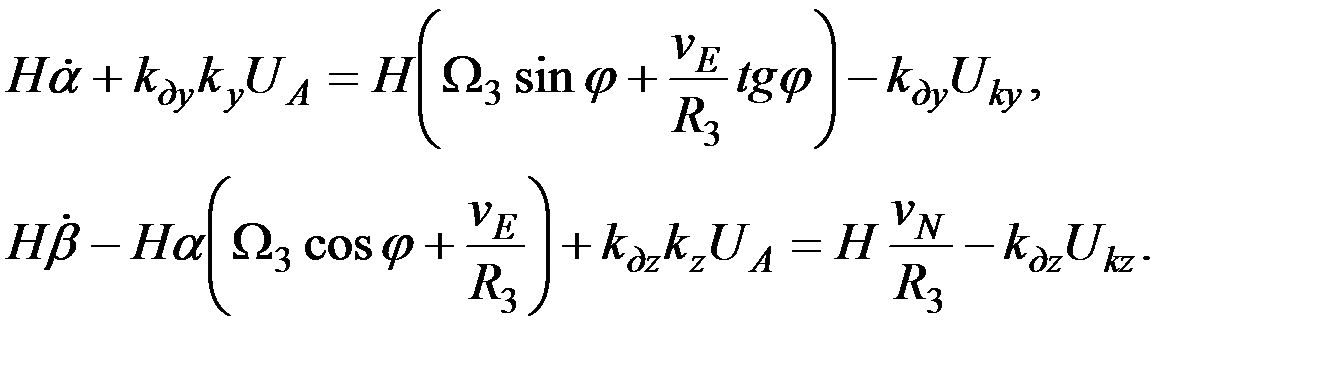(3.9)

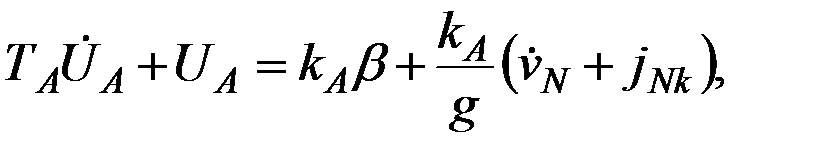
Используя полученные уравнения, проведем исследование основных особенностей поведения чувствительного элемента рассматриваемого гирокомпаса. Как и ранее, в начале проанализируем работу гирокомпаса на судне, движущемся с постоянной скоростью.

<36 373839 40 41 42 >

Дата добавления: 2017-02-13; просмотров: 3033;